A follow-up paper to the one I discussed in my previous post is One-Shot Visual Imitation Learning via Meta-Learning. The idea is, again, to train neural network parameters \(\theta\) on a distribution of tasks such that the parameters are easy to fine-tune to new tasks sampled from the distribution. In this paper, the focus is on imitation learning from raw pixels and showing the effectiveness of a one-shot imitator on a physical PR2 robot.

Recall that the original MAML paper showed the algorithm applied to supervised regression (for sinusoids), supervised classification (for images), and reinforcement learning (for MuJoCo). This paper shows how to use MAML for imitation learning, and the extension is straightforward. First, each imitation task \(\mathcal{T}_i \sim p(\mathcal{T})\) contains the following information:

• A trajectory \(\tau = \{o_1,a_1,\ldots,o_T,a_T\} \sim \pi_i^*\) consists of a sequence of states and actions from an expert policy \(\pi_i^*\). Remember, this is imitation learning, so we can assume an expert. Also, note that the expert policy is task-specific.

• A loss function \(\mathcal{L}(a_{1:T},\hat{a}_{1:T}) \to \mathbb{R}\) providing feedback on how closely our actions match those of the expert’s.

Since the focus of the paper is on “one-shot” learning, we assume we only have one trajectory available for the “inner” gradient update portion of meta-training for each task \(\mathcal{T}_i\). However, if you recall from MAML, we actually need at least one more trajectory for the “outer” gradient portion of meta-training, as we need to compute a “validation error” for each sampled task. This is not the overall meta-test time evaluation, which relies on an entirely new task sampled from the distribution (and which only needs one trajectory, not two or more). Yes, the terminology can be confusing. When I refer to “test time evaluation” I always refer to when we have trained \(\theta\) and we are doing few-shot (or one-shot) learning on a new task that was not seen during training.

All the tasks in this paper use continuous control, so the loss function for optimizing our neural network policy \(f_\theta\) can be described as:

\[\mathcal{L}_{\mathcal{T}_i}(f_\theta) = \sum_{\tau^{(j)} \sim p(\mathcal{T}_i)} \sum_{t=1}^T \| f_\theta(o_t^{(j)}) - a_t^{(j)} \|_2^2\]

where the first sum normally has one trajectory only, hence the “one-shot learning” terminology, but we can easily extend it to several sampled trajectories if our task distribution is very challenging. The overall objective is now:

\[{\rm minimize}_\theta \sum_{\mathcal{T}_i\sim p(\mathcal{T})} \mathcal{L}_{\mathcal{T}_i} (f_{\theta_i'}) = \sum_{\mathcal{T}_i\sim p(\mathcal{T})} \mathcal{L}_{\mathcal{T}_i} \Big(f_{\theta - \alpha \nabla_\theta \mathcal{L}_{\mathcal{T}_i}(f_\theta)}\Big)\]

and one can simply run Adam to update \(\theta\).

This paper uses two new techniques for better performance: a two-headed architecture, and a bias transformation.

• Two-Headed Architecture. Let \(y_t^{(j)}\) be the vector of post-activation values just before the last fully connected layer which maps to motor torques. The last layer has parameters \(W\) and \(b\), so the inner loss function \(\mathcal{L}_{\mathcal{T}_i}(f_\theta)\) can be re-written as:

  \[\mathcal{L}_{\mathcal{T}_i}(f_\theta) = \sum_{\tau^{(j)} \sim p(\mathcal{T}_i)} \sum_{t=1}^T \| Wy_t^{(j)} + b- a_t^{(j)} \|_2^2\]

  where, I suppose, we should write \(\phi = (\theta, W, b)\) and re-define \(\theta\) to be all the parameters used to compute \(y_t^{(j)}\).

  In this paper, the test-time single demonstration of the new task is normally provided as a sequence of observations (images) and actions. However, they also experiment with the more challenging case of removing the provided actions for that single test-time demonstration. They simply remove the action and use this inner loss function:

  \[\mathcal{L}_{\mathcal{T}_i}(f_\theta) = \sum_{\tau^{(j)} \sim p(\mathcal{T}_i)} \sum_{t=1}^T \| Wy_t^{(j)} + b\|_2^2\]

  This is still a bit confusing to me. I’m not sure why this loss function leads to the desired outcome. It’s also a bit unclear how the two-headed architecture training works. After another read, maybe only the \(W\) and \(b\) are updated in the inner portion?

  The two-headed architecture seems to be beneficial on the simulated pushing task, with performance improving by about 5-6 percentage points. That may not sound like a lot, but this was in simulation and they were able to test with 444 total trials.

  The other confusing part is that if we assume we’re allowed to have access to expert actions, then the real-world experiment actually used the single-headed architecture, and not the two-headed one. So there wasn’t a benefit to the two-headed one assuming we have actions. Without actions, of course, the two-headed one is our only option.

• Bias Transformation. After a certain neural network layer (which in this paper is after the 2D spatial softmax applied after the convolutions to process the images), they concatenate this vector of parameters. They claim that

  […] the bias transformation increases the representational power of the gradient, without affecting the representation power of the network itself. In our experiments, we found this simple addition to the network made gradient-based meta-learning significantly more stable and effective.

  However, the paper doesn’t seem to show too much benefit to using the bias transformation. A comparison is reported in the simulated reaching task, with a dimension of 10, but it could be argued that performance is similar without the bias transformation. For the two other experimental domains, I don’t think they reported with and without the bias transformation.

  Furthermore, neural networks already have biases. So is there some particular advantage to having more biases packed in one layer, and furthermore, with that layer being the same spot where the robot configuration is concatenated with the processed image (like what people do with self-supervision)? I wish I understood. The math that they use to justify the gradient representation claim makes sense; I’m just missing a tiny step to figure out its practical significance.

They ran their setups on three experimental domains: simulated reaching, simulated pushing, and (drum roll please) real robotic tasks. For these domains, they seem to have tested up to 5.5K demonstrations for reaching and 8.5K for pushing. For the real robot, they used 1.3K demonstrations (ouch, I wonder how long that took!). The results certainly seem impressive, and I agree that this paper is a step towards generalist robots.

One of the recent landmark papers in the area of meta-learning is MAML: Model-Agnostic Meta-Learning. The idea is simple yet surprisingly effective: train neural network parameters \(\theta\) on a distribution of tasks so that, when faced with a new task, can be rapidly adjusted through just a few gradient steps. In this post, I’ll briefly go over the notation and problem formulation for MAML, and meta-learning more generally.

Here’s the notation and setup, mostly following the paper:

• The overall model \(f_\theta\) is what MAML is optimizing, with parameters \(\theta\). We denote \(\theta_i'\) as weights that have been adapted to the \(i\)-th task through one or more gradient steps. Since MAML can be applied to classification, regression, reinforcement learning, and imitation learning (plus even more stuff!) we generically refer to \(f_\theta\) as mapping from inputs \(x_t\) to outputs \(a_t\).

• A task \(\mathcal{T}_i\) is defined as a tuple \((T_i, q_i, \mathcal{L}_{\mathcal{T}_i})\), where:

  • \(T_i\) is the time horizon. For (IID) supervised learning problems like classification, \(T_i=1\). For reinforcement learning and imitation learning, it’s whatever the environment dictates.

  • \(q_i\) is the transition distribution, defining a prior over initial observations \(q_i(x_1)\) and the transitions \(q_i(x_{t+1}\mid x_{t},a_t)\). Again, we can generally ignore this for simple supervised learning. Also, for imitation learning, this reduces to the distribution over expert trajectories.

  • \(\mathcal{L}_{\mathcal{T}_i}\) is a loss function that maps the sequence of network inputs \(x_{1:T}\) and outputs \(a_{1:T}\) to a scalar value indicating the quality of the model. For supervised learning tasks, this is almost always the cross entropy or squared error loss.

• Tasks are drawn from some distribution \(p(\mathcal{T})\). For example, we can have a distribution over the abstract concept of doing well at “block stacking tasks”. One task could be about stacking blue blocks. Another could be about stacking red blocks. Yet another could be stacking blocks that are numbered and need to be ordered consecutively. Clearly, the performance of meta-learning (or any alternative algorithm, for that matter) on optimizing \(f_\theta\) depends on \(p(\mathcal{T})\). The more diverse the distribution’s tasks, the harder it is for \(f_\theta\) to quickly learn new tasks.

The MAML algorithm specifically finds a set of weights \(\theta\) that are easily fine-tuned to new, held-out tasks (for testing) by optimizing the following:

\[{\rm minimize}_\theta \sum_{\mathcal{T}_i\sim p(\mathcal{T})} \mathcal{L}_{\mathcal{T}_i} (f_{\theta_i'}) = \sum_{\mathcal{T}_i\sim p(\mathcal{T})} \mathcal{L}_{\mathcal{T}_i} \Big(f_{\theta - \alpha \nabla_\theta \mathcal{L}_{\mathcal{T}_i}(f_\theta)}\Big)\]

This assumes that \(\theta_i' = \theta - \alpha \nabla_\theta \mathcal{L}_{\mathcal{T}_i}(f_\theta)\). It is also possible to do multiple gradient steps, not just one. Thus, if we do \(K\)-shot learning, then \(\theta_i'\) is obtained via \(K\) gradient updates based on the task. However, “one shot” is cooler than “few shot” and also easier to write, so we’ll stick with that.

Let’s look at the loss function above. We are optimizing over a sum of loss functions across several tasks. But we are evaluating the (outer-most) loss functions while assuming we made gradient updates to our weights \(\theta\). What if the loss function were like this:

\[{\rm minimize}_\theta \sum_{\mathcal{T}_i\sim p(\mathcal{T})} \mathcal{L}_{\mathcal{T}_i} (f_{\theta})\]

This means \(f_\theta\) would be capable of learning how to perform well across all these tasks. But there’s no guarantee that this will work on held-out tasks, and generally speaking, unless the tasks are so closely related, it shouldn’t work. (I’ve tried doing some similar stuff in the past with the Atari 2600 benchmark where a “task” was “doing well on game X”, and got networks to optimize across several games, but generalization was not possible without fine-tuning.) Also, even if we were allowed to fine-tune, it’s very unlikely that one or few gradient steps would lead to solid performance. MAML should do better precisely because it optimizes \(\theta\) so that it can adapt to new tasks with just a few gradient steps.

MAML is an effective algorithm for meta-learning, and one of its advantages over other algorithms such as \({\rm RL}^2\) is that it is parameter-efficient. The gradient updates above do not introduce extra parameters. Furthermore, the actual optimization over the full model \(\theta\) is also done via SGD

\[\theta = \theta - \beta \left( \nabla_\theta \sum_{\mathcal{T}_i\sim p(\mathcal{T})} \mathcal{L}_{\mathcal{T}_i} \Big(f_{\theta - \alpha \nabla_\theta \mathcal{L}_{\mathcal{T}_i}(f_\theta)}\Big) \right)\]

again introducing no new parameters. (The update is actually Adam if we’re doing supervised learning, and TRPO if doing RL, but SGD is the foundation of those and it’s easier for me to write the math. Also, even though the updates may be complex, I think the inner part, where we have \(f_{\theta - \alpha \nabla_\theta \mathcal{L}_{\mathcal{T}_i}(f_\theta)}\), I think that is always vanilla SGD, but I could be wrong.)

I’d like to emphasize a key point: the above update mandates two instances of \(\mathcal{L}_{\mathcal{T}_i}\). One of these — the one in the subscript to get \(\theta_i'\) should involve the \(K\) training instances from the task \(\mathcal{T}_i\) (or more specifically, \(q_i\)). The outer-most loss function should be computed on testing instances, also from task \(\mathcal{T}_i\). This is important because we want our ultimate evaluation to be done on testing instances.

Another important point is that we do not use those “testing instances” for evaluating meta-learning algorithms, as that would be cheating. For testing, one takes a held-out set of test tasks entirely, adjusts \(\theta\) for however many steps are allowed (one in the case of one-shot learning, etc.) and then evaluates according to whatever metric is appropriate for the task distribution.

In a subsequent post, I will further investigate several MAML extensions.

In this post, I will further investigate one of the papers I discussed in an earlier blog post: Zero-Shot Visual Imitation (Pathak et al., 2018).

For notation, I denote states and actions at some time step \(t\) as \(s_t\) and \(a_t\), respectively, if they were obtained through the agent exploring in the environment. A hat symbol, \(\hat{s}_t\) or \(\hat{a}_t\), refers to a prediction made from some machine learning model.

Basic forward (left) and inverse (right) model designs.

Recall the basic forward and inverse model structure (figure above). A forward model takes in a state-action pair and predicts the subsequent state \(\hat{s}_{t+1}\). An inverse model takes in a current state \(s_t\) and some goal state \(s_g\), and must predict the action that will enable the agent go from \(s_t\) to \(s_t\).

• It’s easiest to view the goal input to the inverse model as either the very next state \(s_{t+1}\), or the final desired goal of the trajectory, but some papers also use \(s_g\) as an arbitrary checkpoint (Agrawal et al., 2016, Nair et al., 2017, Pathak et al., 2018). For the simplest model, it probably makes most sense to have \(s_g = s_{t+1}\) but I will use \(s_g\) to maintain generality. It’s true that \(s_g\) may be “far” from \(s_t\), but the inverse model can predict a sequence of actions if needed.

• If the states are images, these models tend to use convolutions to get a lower dimensional featurized state representation. For instance, inverse models often process the two input images through tied (i.e., shared) convolutional weights to obtain \(\phi(s_t)\) and \(\phi(s_{t+1})\), upon which they’re concatenated and then processed through some fully connected layers.

As I discussed earlier, there are a number of issues related to this basic forward/inverse model design, most notably about (a) the high dimensionality of the states, and (b) the multi-modality of the action space. To be clear on (b), there may be many (or no) action(s) that let the agent go from \(s_t\) to \(s_g\), and the number of possibilities increases with a longer time horizon, if \(s_g\) is many states in the future.

Let’s understand how the model proposed in Zero-Shot Visual Imitation mitigates (b). Their inverse model takes in \(s_g\) as an arbitrary checkpoint/goal state and must output a sequence of actions that allows the agent to arrive at \(s_g\). To simplify the discussion, let’s suppose we’re only interested in predicting one step in the future, so \(s_g = s_{t+1}\). Their predictive physics design is shown below.

The basic one-step model, assuming that our inverse model just needs to predict one action. The convolutional layers for the inverse model use the same tied network convolutional weights. The action loss is the cross-entropy loss (assuming discrete actions), and is not written in detail due to cumbersome notation.

The main novelty here is that our predicted action \(\hat{a}_t\) from the inverse model is provided as input to the forward model, along with the current state \(s_t\). We then try and obtain \(s_{t+1}\), the actual state that was encountered during the agent’s exploration. This loss \(\mathcal{L}(s_{t+1}, \hat{s}_{t+1})\) is the standard Euclidean distance and is added with the action prediction loss \(\mathcal{L}(a_t,\hat{a}_t)\) which is the usual cross-entropy (for discrete actions).

Why is this extra loss function from the successor states used? It’s because we mostly don’t care which action we took, so long as it leads to the desired next state. Thus, we really want \(\hat{s}_{t+1} \approx s_{t+1}\).

Two extra long-ended comments:

• There’s some subtlety with making this work. The state loss \(\mathcal{L}(s_{t+1}, \hat{s}_{t+1})\) treats \(s_{t+1}\) as ground truth, but that assumes we took action \(a_t\) from state \(s_t\). If we instead took \(\hat{a}_t\) from \(s_t\), and \(\hat{a}_t \ne a_t\), then it seems like the ground-truth should no longer be \(s_{t+1}\)?

  Assuming we’ve trained long enough, then I understand why this will work, because the inverse model will predict \(\hat{a}_t = a_t\) most of the time, and hence the forward model loss makes sense. But one has to get to that point first. In short, the forward model training must assume that the given action will actually result in a transition from \(s_t\) to \(s_{t+1}\).

  The authors appear to mitigate this with pre-training the inverse and forward models separately. Given ground truth data \(\mathcal{D} = \{s_1,a_1,s_2,\ldots,s_N\}\), we can pre-train the forward model with this collected data (no action predictions) so that it is effective at understanding the effect of actions.

  This would also enable better training of the inverse model, which (as the authors point out) depends on an accurate forward model to be able to check that the predicted action \(\hat{a}_t\) has the desired effect in state-space. The inverse model itself can also be pre-trained entirely on the ground-truth data while ignoring \(\mathcal{L}(s_{t+1}, \hat{s}_{t+1})\) from the training objective.

  I think this is what the authors did, though I wish there were a few more details.

• A surprising aspect of the forward model is that it appears to predict the raw states \(s_{t+1}\), which could be very high-dimensional. I’m surprised that this works, given that (Agrawal et al., 2016) explicitly avoided this by predicting lower-dimensional features. Perhaps it works, but I wish the network architecture was clear. My guess is that the forward model processes \(s_t\) to be a lower dimensional vector \(\psi(s_t)\), concatenates it with \(\hat{a}_t\) from the inverse model, and then up-samples it to get the original image. Brandon Amos describes up-sampling in his excellent blog post. (Note: don’t call it “deconvolution.”)

Now how do we extend this for multi-step trajectories? The solution is simple: make the inverse model a recurrent neural network. That’s it. The model still predicts \(\hat{a}_t\) and we use the same loss function (summing across time steps) and the same forward model. For the RNN, the convolutional layers \(\phi\) take in the current state but they always take in \(s_g\), the goal state. They also take in \(h_{i-1}\) and \(a_{i-1}\) the previous hidden unit and the previous action (not the predicted action, that would be a bit silly when we have ground truth).

The multi-step trajectory case, visualizing several steps out of many.

Thoughts:

• Why not make the forward model recurrent?

• Should we weigh shorter-term actions highly instead of summing everything equally as they appear to be doing?

• How do we actually decide the length of the action vector to predict? Or said in a better way, when do we decide that we’ve attained \(s_g\)?

Fortunately, the authors answer that last thought by training a deep neural network that can learn a stopping criterion. They say:

We sample states at random, and for every sampled state make positives of its temporal neighbors, and make negatives of the remaining states more distant than a certain margin. We optimize our goal classifier by cross-entropy loss.

So, states “close” to each other are positive samples, whereas “father” samples are negative. Sure, that makes sense. By distance I assume simple Euclidean distance on raw pixels? I’m generally skeptical of Euclidean distance but it might be necessary if the forward model also optimizes the same objective. I also assume this is applied after each time step, testing whether \(s_i\) at time \(i\) has reached \(s_g\). Thus, it is not known ahead of time how many actions the RNN must be able to predict before the goal is reset.

An alternative is mentioned about treating stopping as an action. There’s some resemblance to this and DDO’s option termination criterion.

Additionally, we have this relevant comment on OpenReview:

The independent goal recognition network does not require any extra work concerning data or supervision. The data used to train the goal recognition network is the same as the data used to train the PSF. The only prior we are assuming is that nearby states to the randomly selected states are positive and far away are negative which is not domain specific. This prior provides supervision for obtaining positive and negative data points for training the goal classifier. Note that, no human supervision or any particular form of data is required in this self-supervised process.

Yes, this makes sense.

Now let’s discuss the experiments. The authors test several ablations of their model:

• An inverse model with no forward model at all (Nair et al., 2017). This is different from their earlier paper which used a forward model for regularization purposes (Agrawal et al., 2016). The model in (Nair et al., 2017) just used the inverse model for predicting an action given current image \(I_t\) and (critically!) a goal image \(I_{t+1}'\) specified by a human.

• A more sophisticated inverse model with an RNN, but no forward model. Think of my most recent hand-drawn figure above, except without the forward portion. Furthermore, this baseline also does not use the action \(a_i\) as input to the RNN structure.

• An even more sophisticated model where the action history is now input to the RNN. Otherwise, it is the same as the one I just described above.

Thus, all three of their ablations do not use the forward consistency model and are solely trained by minimizing \(\mathcal{L}(a_t,\hat{a}_t)\). I suppose this is reasonable, and to be fair, testing these out in physical trials takes a while. (Training should be less cumbersome because data collection is the bottleneck. Once they have data, they can train all of their ablations quickly.) Finally, note that all these inverse models take \((s_t,s_g)\) as input, and \(s_g\) is not necessarily \(s_{t+1}\). This, I remember from the greedy planner in (Agrawal et al., 2016).

The experiments are: navigating a short mobile robot throughout rooms and performing rope manipulation with the same setup from (Nair et al., 2017).

• Indoor navigation. They show the model an image of the target goal, and check if the robot can use it to arrive there. This obviously works best when few actions are needed; otherwise, waypoints are necessary. However, for results to be interesting enough, the target image should not have any overlap with the starting image.

  The actions are: (1) forward 10cm, (2) turn left, (3) turn right, and (4) standing still. They use several “tricks” such as using action repeats, applying a reset maneuver, etc. A ResNet acts as the image processing pipeline, and then (I assume) the ResNet output is fed into the RNN along with the hidden layer and action vector.

  Indeed, it seems like their navigating robot can reach goal states and is better than the baselines! They claim their robot learns first to turn and then to move to the target. To make results more impressive, they tested all this on a different floor from where the training data was collected. Nice! The main downside is that they conducted only eight trials for each method, which might not be enough to be entirely convincing.

  Another set of experiments tests imitation learning, where the goal images are far away from the robot, thus mandating a series of checkpoint images specified by a human. Every fifth image in a human demonstration was provided as a waypoint. (Note: this doesn’t mean the robot will take exactly five steps for each waypoint even if it was well trained, because it may take four or six or some other number of actions before it deems itself close enough to the target.) Unfortunately, I have a similar complaint as earlier: I wish there were more than just three trials.

• Rope manipulation. They claim almost a 2x performance boost over (Nair et al., 2017) while using the same training data of 60K-70K interaction pairs. That’s the benefit of building upon prior work. They surprisingly never say how many trials they have, and their table reports only a “bootstrapped standard deviation”. Looking at (Nair et al., 2017), I cannot find where the 35.8% figure comes from (I see 38% in that paper but that’s not 35.8%…).

  According to OpenReview comments they also trained the model from (Agrawal et al., 2016) and claim 44% accuracy. This needs to be in the final version of the paper. The difference from (Nair et al., 2017) is that (Agrawal et al., 2016) jointly train a forward model (but not to enforce dynamics but just as a regularizer), while (Nair et al., 2017) do not have any forward model.

Despite the lack of detail in some areas of the paper, (where’s the appendix?!?) I certainly enjoyed reading it and would like to try out some of this stuff.

I have now run in three half marathons: the Berkeley Half Marathon (November 2017), the Kaiser Permanente San Francisco Half Marathon (February 2018), and the Oakland Half Marathon (March 2018).

To be clear, the Kaiser Permanente San Francisco half marathon is not the same as a separate set of San Francisco races in the summers. The Oakland Half Marathon is also technically the “Kaiser Permanente […]” but since there’s only one main set of Oakland races a year — known as the “Running Festival” — we can be more lenient in our naming convention.

All these races are popular, and the routes are relatively flat and therefore great for setting PRs. I would be happy to run any of these again. In fact, I’ll probably will, for all three!

In this post, I’ll provide some brief comments on each of the races. Note that:

• When I list registration fees, it’s not always a clear-cut comparison since prices jack up closer to race day. I think I managed to get an “early bird” deal for all these races, so hopefully the prices are somewhat comparable. Also, I include taxes in the fee I list.

• By “packet pickup” I refer to when runners pick up whatever racing material is needed (typically a timing chip, bib, sometimes gear as well) a day or two before the actual race. These pickup events also involve some deals for food and running equipment from race sponsors. Below is a picture that I took of the Oakland package pickup:

  
  

• While I list “pros” and “cons” of the races, most are minor in the grand scheme of things, and this review is for those who might be picky. I reiterate that I will probably run in all of these again the next time around.

OK, let’s get started!

Berkeley Half Marathon

• Website: here.
• Price I paid: about 100 dollars, including a 10 dollar bib shipping fee.

Pros:

• The race has a great “local feel” to it, with lots of Berkeley students and residents both running in the race or cheering us as spectators. I saw a number of people that I knew, mostly other student runners, and it was nice to say hi to them. There was also a cool drumming band which played while we were entering the portion of the race close to the San Francisco Bay.

• The course is mostly flat, and enters a few Berkeley neighborhoods (again, a great local feel to it). There’s also a relatively straight section at the roughly 8-11 mile range by the San Francisco Bay and which lets you see the runners ahead of you when you’re entering the portion (for extra motivation). As I discussed two years ago, I regularly run by this area so I was used to the view, but I can see it being attractive for those who don’t use the same routes.

• There are lots of pacers, for half-marathon finish times of 1:27, 1:35 (2x), 1:45, 1:55, etc.

• The post-race food sampling selection was fantastic! There were the obligatory water bottles and bananas, but I also had tasty Power Crunch protein bars, Muscle Milk (this is clearly bad for you, but never mind), pretzels, cookies, coffee, etc. There was also beer, but I didn’t have any.

• Post-race deals are excellent. I used them to order some Power Crunch bars at a discount.

• The packet pickup had some decent free food samples. The race shirt is interesting — it’s a different style from prior years and feels somewhat odd but I surprisingly like it, and I’ll be wearing it both to school and for when I run in my own time.

Cons:

• There’s a $10 bib mailing fee, and I realize now that it’s pointless to pay for it because we also have to pick up a timing chip during packet pickup, and that’s when we could have gotten the bibs. Thus, there seems to be no advantage to paying for the bib to be mailed. Furthermore, I wish the timing chip were attached to the bib; we had to tie it within our shoelaces. I think it’s far easier to stick it on the bib.

• The starting location is a bit awkwardly placed in the center of the city, though to be fair, I’m not sure of a better spot. Certainly it’s less convenient for drop-offs and Uber rides compared to, say, Golden Gate Park.

• There were seven water stops, one of which had electrolytes and GU energy chews. (Unfortunately, when running, I actually dropped two out of the four GU chews I was given … please use the longer, thinner packages that the Oakland race uses!!) The other two races offered richer goodies at the aid stations so next time, I’ll bring my own energy stuff.

• It was the most expensive of the races I’ve run in, though the difference isn’t that much, especially if you avoid making the mistake of getting your bib mailed to you.

• The photography selection after the race is excellent, but it’s expensive and most of it is concentrated near the end of the race when it’s crowded, so most pictures weren’t that interesting.

Kaiser Permanente San Francisco Half Marathon

• Website: here.
• Price I paid: about $80.

Upsides:

• The race route is great! I enjoyed running through Golden Gate Park and seeing the Japanese Tea Garden, the California Academy of Sciences, and so on. There’s also a very long, straight section in the second half of the race (longer than Berkeley’s!) by the ocean where you can again see the runners ahead of you on their way back.

• There’s a great selection of post-race sampling, arguably on par with Berkeley though there’s no beer. There were water bottles and bananas, along with CLIF Whey protein bars, Ocho candy, some coffee/caffeine-base drinks, etc.

• The price is the cheapest of the three, which is surprising since I figured things in San Francisco would be more expensive. I suspect it has to do with much of the race being in Golden Gate Park, and the course is set so that there isn’t a need to close many roads. On a related note, it’s also easy to drop off and pick up racers.

• You have to finish the race to get your shirt. Of course this is minor, but I believe it’s not a good idea to wear the official race shirt on race day. Incidentally, there’s no package pickup, which means we don’t get free samples or deals, but it’s probably better for me since I would have had to Uber a long distance to and back. You get the bib and timing chip mailed in advance, and the timing chip is (thankfully) attached to the bib.

Downsides:

• No pacers. I don’t normally try to stick to a pacer during my races, but I think they’re useful.

• While there was a great selection of post-race food sampling, there was no beer offered, in contrast to the Berkeley and Oakland races.

• With regards to post-race photographs, my comments on this are basically identical to those of the Berkeley race.

• All the aid stations had electrolytes (I think Nuun) in addition to water. It was a bit unclear to me which cups corresponded to what beverage, though in retrospect I should have realized that the “blank” cups had water and cups with a lightning sign on them had the electrolytes. The drinks situation is better than the Berkeley race, but the downside is that there were no GU energy chews, so perhaps it’s a wash with respect to the aid stations?

• It felt like there were fewer people cheering us on when we raced, particularly compared to the Berkeley race.

• I don’t think there were as many post-race discount deals. I was hoping that there were some deals for the CLIF whey protein bars, which would have been the analogue of the Power Crunch discount for the Berkeley race. The discount deals also lasted only a week, compared to two months for Berkeley’s post-race stuff.

Oakland Running Festival Half Marathon

• Website: here.
• Price I paid: about $90.

Upsides:

• The race started at 9:45am, whereas the Berkeley and San Francisco races each started at about 8:10am. While I consider myself a morning person, that’s for work. If I want to set a half marathon PR, a 9:45am starting time is far better.

• The Oakland race easily has the best aid stations compared to the other two races. Not only were there electrolytes at each station, but some also had bananas, GU gels, and GU chews (yes, GU has a lot of products!). Throughout the race I consumed two half-bananas (easy to eat since you can squeeze them), one GU gel, and one GU chew package, which contained about eight chews. This was very helpful!

• There were lots of spectators and locals cheering us on, possibly as much as the Berkeley race had.

• The view of Lake Merritt is excellent, and it’s probably the main visual attraction. Other than that, the race enters the city of Oakland throughout mostly the business sector. Also this was the only one of the three races where a marathon was simultaneously offered, so there were a few marathoners mixed in with us.

• There’s a great package pickup (which I showed a photo of earlier), which probably had as many deals as the Berkeley package pickup. We had to show up to the pickup to get the bib and the timing chip (attached to the bib). While I was there, I bought several GU products that I’ll use for my future long-distance training sessions.

• Each runner got tickets for two free Lagunitas Beer cups. We had this offering after the race, but one was enough for me. I’m not sure how people can down two servings quickly.

• There were pacers for various distances.

• Race photos are free, which is definitely refreshing compared to the other two races. Disclaimer: I’m writing this post one day after the race occurred, and I won’t be able to download the photos for a few days, so the quality may be worse on a per-photo basis.

• Unfortunately, I don’t think there are any post-race deals. Hopefully something will show up in my inbox soon so I can turn this into an “upside.” Update 03/27/2018: heh, a day later, I get an email in my inbox showing that there are some race deals. Excellent! The deals seems to be just as good as the other races, so I’ll put it as an upside.

Downsides:

• The race scenery is probably less appealing than the Berkeley or San Francisco races. The route mostly weaves throughout the city roads, and there aren’t clear views of the Bay. Also, the turn near the end of the race when we see Lake Merritt again is narrow and awkwardly placed, and it’s also hilly, which is not what I want to see at the 12th and 13th mile checkpoints.

• The post-race food sampling was probably weaker compared to the other two, though it’s debatable. There were water bottles, as you can see in my photo below, along with bananas and some peanut butter bars and energy drinks. I think the other races had more, and I was disappointed when the Oakland website said that racers would “receive bagels” because I didn’t see any! On the positive side, I got a free package of GU stroopwafel, so again, it’s debatable.

• The race isn’t as good at storing your sweats. At Berkeley, we could save our sweats in the Berkeley high school gym, and it was easy for us to retrieve our bags after the race. For Oakland, it was stored in a small tent and we had to stand in line for a while before a volunteer could find our stuff.

The finish line of the Oakland races (including the half marathon).

Conclusion

I’m really happy that I started running half marathons. I’m signed up to run the San Francisco Second Half-Marathon in July. If you’re interested in training with me, let me know.

I enjoy reading robotics and deep reinforcement learning papers that cleverly apply self-supervision to learn some task. There’s something oddly appealing about an agent “semi-randomly” acting in a world and learning something useful out of the data it collects. Some papers, for instance, build visual predictive models, which are those that enable the agent to anticipate the future states of the world, which may be raw images (or more commonly, a latent feature representation of them). Said another way, the agent learns an internal physics model. The agent can then use it to plan because it knows the effect of its actions, so it can run internal simulations and pick the action that results in the most desirable outcome.

In this blog post, I’ll discuss a few papers about self-supervision and visual predictive models by providing a brief description of their contributions. A subsequent blog post will discuss the papers’ relationships to each other in further detail.

Paper 1: Learning Visual Predictive Models of Physics for Playing Billiards (ICLR 2016)

“Billiards” in this paper refers to a generic, 2-D simulated environment of balls that move and bounce around walls according to the laws of physics. As the authors correctly point out, this is an environment that easily enables extensive experiments: altering the number of balls, changing their sizes or colors, and so forth.

While the agent “sees” a 2-D image of the environment, that is not the direct input to the neural network nor is it what the neural network predicts.

• The input consists of the past four “glimpses” of the object, and the applied forces (which we assume known and tracked). The glimpses should be the 128x128 RGB image of the environment, but perhaps “blacking out” everything except the object. (I’m not sure about the technical details, but the idea is intuitive.) Thus, the same network is used for each of the balls in the environment, which the authors call an “object-centric” model. As one would expect, the input image is passed through a series of convolutional layers and then the forces are concatenated with that feature representation.

• The output is the object’s predicted velocity for the current and subsequent (up to \(h\)) times. It is not the standard latent feature representation that other visual predictive models normally apply, because in billiards, they assume it is enough to know the displacements of the balls to track them.

The model is trained by minimizing

\[\sum_{k=1}^h w_k\|\tilde{u}_{t+k} - u_{t+k}\|_2^2\]

where \(w_k\) is a weighing factor that is larger for shorter-term (smaller \(k\)) time steps. Good, this makes sense.

The authors show that they are able to predict the trajectories of balls, and that this can be generalized and also used for planning.

Paper 2: Learning to Poke by Poking: Experiental Learning of Intuitive Physics (NIPS 2016)

I discussed this paper in a previous blog post. Heh, you can tell that I’m interested in this stuff.

Paper 3: Learning Hand-Eye Coordination for Robotic Grasping with Deep Learning and Large-Scale Data Collection (IJRR 2017)

This is the famous (or infamous?) “arm-farm” paper from Google. The dataset here is MASSIVE — I don’t know of a self-supervision paper with real robots that contains this much data. The authors collected 800,000 (semi-)random grasp attempts collected over two months by running up to 14 robots in parallel. In fact, even this somewhat understates the total amount of data: each grasp consists of \(T\) training data points of the form \((I_t^i, p_T^i - p_t^i, \ell_i)\) which contains the current camera image, the vector from the current pose to the one that is eventually reached, and the success of the grasp.

The data then enables the robot to effectively learn hand-eye coordination by continuous visual servoing, without the need for camera calibration. Given a camera image of the workspace, and independently of the calibration or robot pose, the trained CNN predicts the probability that the motion of the gripper results in successful grasps.

During data collection, the labels (either a successful grasp or not) must be automatically supplied. The authors do this with (a) checking if the gripper closed or not, and (b) an image subtraction test, testing the image before and after the object was grasped. This makes sense to me. The first test is used, and then the second is a backup to check for small objects. I can see how it might fail, though, such as if the robot grasped the wrong object or pushed the target object to the side rather than picking it up, either of which would result in a different image than the starting one

The use of robots running in parallel means that each can collect a diverse dataset on its own, in part due to different actions and in part due to different material properties of each gripper. This is an application of the A3C concept from Deep Reinforcement Learning for real, physical robotics.

There are a lot of things that I like from this paper, but one that really seems intriguing for future AI applications is that the data enabled the robots to learn different grasping strategies for different types of objects, such as the soft vs hard difference the authors observed.

Paper 4: Learning to Act by Predicting the Future (ICLR 2017)

I discussed this paper in a previous blog post.

Paper 5: Combining Self-Supervised Learning and Imitation for Vision-Based Rope Manipulation (ICRA 2017)

The same architectural idea from the “Learning to Poke” paper is used in this one to jointly learn forward and inverse dynamics models. Instead of poking, the robot learns rope manipulation, a complicated task to model with hard-coded physics.

In my opinion, one of the weaknesses in the “Learning to Poke” paper was the greedy planner. The planner saw the current and goal images, and had to infer the intermediate actions. This prevented the robot from learning longer-horizon tasks, because the goal image could be quite different from the current one. In this paper, the authors allow for longer-horizon learning by providing one human demonstration of the task. The demonstration consists of a sequence of images, each of which are repeatedly fed into the neural network model at each time step. Thus, the goal image should be the one that correspond to the next time step, which appears to be more tractable.

They ran their Baxter robot autonomously for 500 hours, collecting 60,000 training data points.

Paper 6: Curiosity-Driven Exploration by Self-Supervised Prediction (ICML 2017)

They build on top of an existing RL algorithm, A3C, by modifying the reward function so that at each time step \(t\), the reward is \(r_t^{i}+r_t^{e}\) instead of just \(r_t^{e}\), where \(r_t^{i}\) is the curiosity reward and \(r_t^{e}\) is the reward from the environment.

In sparse rewards, such as the Doom environment from OpenAI they use (and, I might add, the recent robotics environments, also from OpenAI) the environment reward is zero almost everywhere, except for 1 at the goal. This makes it effectively an intractable problem for off-the-shelf RL algorithms. Hence, by building a predictive model, given current and subsequent states \(s_t\) and \(s_{t+1}\) they can assign the curiosity reward to be

\[r_t^i = \frac{\eta}{2}\|\hat{\phi}(s_{t+1}) - \phi(s_{t+1})\|_2^2\]

which measures the difference in the predicted latent space of the successor state, respectively. The inverse dynamics model takes in \((s_t,s_{t+1})\) during training and predicts \(a_t\). The forward dynamics model predicts the latent successor state \(\hat{\phi}(s_{t+1})\) shown above.

They argue that their form of curiosity has three benefits: solving tasks with sparse rewards, exploring the environment, and learning skills that can be reused and applied in different scenarios. One interesting conjecture from the third claim is that if the agent simply does the same thing over and over again, the curiosity reward will go down to zero because the agent is stuck in the same latent space. Only by “learning” new actions that substantially change the latent space will the agent then be able to obtain new rewards.

The results on Doom and Mario environments are impressive.

Paper 7: Zero-Shot Visual Imitation (ICLR 2018)

Wait, zero-shot visual imitation (learning)? How is this possible?

First, let’s be clear on their technical definition: “zero-shot” means that they are still allowed to observe a demonstration of the task, but it has to be only the state space (i.e., images), so actions are not included. The second part of the definition means that expert demonstrations (regardless of states or actions) are not allowed during training.

OK, that makes sense. So … the robot just sees the images of the demo at inference time, and must imitate it. That’s a high bar. The key must be to develop a sufficient prior — but how? By having the agent move (semi-)randomly to learn physics, of course!

In terms of the visual predictive model, the paper does a nice job describing four different models, starting from the ICRA 2017 rope manipulation paper and moving towards the one they use for their experiments. Their final model conditions on the final goal and uses recurrent neural networks, and is augmented with a separate neural network that predicts whether the goal has been attained or not.

The paper presents two sets of experiments. One is a navigation task using a mobile robot, and the other is a rope manipulation task using the Baxter robot. With zero-shot visual imitation, the Baxter robot doubles the performance of rope manipulation compared to the results from ICRA 2017. Thus, if I’m thinking about rope manipulation benchmarks, I better check out this paper and not the ICRA 2017 one. I also assume that zero-shot visual imitation would result in better poking performance than “Learning to Poke” if the poking requires long-term planning.

Results for the navigation agent are also impressive.

This is not a deep reinforcement learning paper, though one could argue for the use of Deep RL as an alternative to self-supervision. Indeed, that was a point raised by one of the reviewers.

Additional References

Here are a few additional papers that are somewhat related to the above, and which I don’t have time to write about in detail … yet.

• Unsupervised Learning for Physical Interaction through Video Prediction is another interesting paper on imagining the future based on predicting pixel motion.

• One-Shot Visual Imitation Learning via Meta-Learning allows robots to learn how to perform tasks with a single demonstration. It’s somewhat related to the “Zero-Shot Visual Imitation” paper, except those papers use very different solutions for different problems. I’d like to compare them in more detail later.

• Reinforcement Learning with Unsupervised Auxiliary Tasks works by having a reinforcement learning agent consider a series of “pseudo” loss functions that it considers under its objective function.

• Diversity is All You Need, which argues that by using entropy correctly, an agent can automatically learn useful skills in an environment. It’s related to the “Curiosity” paper in discovering new skills.

As I write this post, UC Berkeley is hosting its “visit days” program for admitted EECS PhD students. This is a three-day event that lets admitted students see the department, meet people, and get a (tiny) flavor of what Berkeley is like. Those interested in some history may enjoy my blog post about visit days four years ago.

If you’re an admitted student, congratulations! It’s super-competitive to get in. When I applied, the acceptance rate was roughly 5 percent, and the competition has undoubtedly increased since then. This is definitely true for those applying to work in Artificial Intelligence. I’ve seen statistics from BAIR director Trevor Darrell showing that the number of AI applicants has soared in recent years, to the point where the corresponding acceptance rate is now less than three percent.

It’s technically true that you’re not tied to a specific area when you apply, and that’s what the department probably advertises to admitted students. Do not, however, take this as implying that you can apply in an area you’re not interested in but think is “less competitive” and then pivot to AI. If you want to do fundamental AI research (and not just use it in an application) you must apply in AI — otherwise, I highly doubt the faculty will be interested in working with you when they already have the cream of the crop to consider from other applicants.

That being said, here are some related thoughts regarding graduate school, visit days, and so forth, which might be of use to admitted students:

• You must come to visit days. You will learn a lot about the professors who are interested in working with you based on your assigned one-on-one meetings. I don’t know the details on how those assignments are made, but it’s a good bet that if a professor wants to work with you, then you’ll have a one-on-one meeting with him or her.

• On a related note, if there’s a faculty member you desperately want to work with, then not only do you need to talk to him or her during visit days, you also need a firm commitment that he or she is willing to advise you without qualifications. This is particularly true for the “rock-star” faculty who get swarmed with emails from top-tier students asking to work with them. Get commitments done early.

• You also want to be in touch with the students in your target lab(s). If you accept your offer, consistently communicate with them well before the official start of your PhD. This might mean just occasional emails over the summer, or (better) being remotely involved in an ongoing research project that can lead to a fast paper during your first semester. The point is, you want to be in the loop in what the other students are doing. This also includes incoming students — you’ll want to take the same classes as those in your research area, so that you can collaborate on homework and (ideally) research.

These previous points imply the following: you do not want to be spending your first year (or two) trying to “explore” or “get incubated” into research. Your goal must be to do outstanding research in your area of interest from day one.

It’s easy to experience euphoria upon getting your offer of admission. I don’t mean to rain on this, but there’s life beyond getting the admitted offer, and you want to make a sound and informed decision on something that will impact you forever. Again, if you got accepted to Berkeley, congratulations! I hope you seriously consider attending, as it’s one of the top computer science schools. Just ensure that you were admitted to your area of interest, and furthermore, it is crystal clear that the professors who you want to work with are willing to advise you from day one.

One of the things I’m most excited about nowadays is that physical robots now have the capability to repeatedly execute trajectories to gather data. This can then be fed into a learning algorithm to subsequently learn complex manipulation tasks. In this post, I’ll talk about a paper which does exactly that: the NIPS 2016 paper Learning to Poke by Poking: Experiental Learning of Intuitive Physics. (arXiv link; project website) Yes, it’s experiental, not experimental, which I originally thought was a typo, heh.

The main idea of the paper is that by repeatedly poking objects, a robot can then “learn” (via Deep Learning) an internal model of physics. The motivation for the paper came out of how humans seem to possess this “internal physics” stuff:

Humans can effortlessly manipulate previously unseen objects in novel ways. For example, if a hammer is not available, a human might use a piece of rock or back of a screwdriver to hit a nail. What enables humans to easily perform such tasks that machines struggle with? One possibility is that humans possess an internal model of physics (i.e. “intuitive physics” (Michotte, 1963; McCloskey, 1983)) that allows them to reason about physical properties of objects and forecast their dynamics under the effect of applied forces.

I think it’s a bit risky to try and invoke human reasoning in a NIPS paper, but it seems to have worked out here (and the paper has been cited a fair amount).

The methodology can be summarized as:

In our setup (see Figure 1), a Baxter robot interacts with objects kept on a table in front of it by randomly poking them. The robot records the visual state of the world before and after it executes a poke in order to learn a mapping between its actions and the accompanying change in visual state caused by object motion. To date our robot has interacted with objects for more than 400 hours and in process collected more than 100K pokes on 16 distinct objects.

Now, how does the Deep Learning stuff work to actually develop this internal model? To describe this, we need to understand two things: the data collection and the neural network architecture(s).

First, for data collection, they randomly poke objects in a workstation and collect the tuple of: before image, after image, and poke. The first two are just the images from the robot sensors and the “poke” is a tuple with information about the poke point, direction and length. Second, they train two models: a forward model to predict the next state given the current state and the applied force, and an inverse model to predict the action given the initial and target state. A state, incidentally, could be the raw image from the robot’s sensors, or it could be some processed version of it.

I’d like to go through the architecture in more detail. If we assume naively that the forward and inverse models are trained separately, we get something like this:

Visualization of the forward and inverse models. Here, we assume the forward and inverse models are trained separately. Thus, the forward model takes a raw image and action as input, and has to predict the full image of the next state. In the inverse model, the start and goal images are input, and it needs to predict the action that takes the environment to the goal image.

where the two models are trained separately and act on raw images from the robot’s sensors (perhaps 1080x1080 pixels).

Unfortunately, this kind of model has a number of issues:

• In the forward model, predicting a full image is very challenging. It is also not what we want. Our goal is for forward model to predict a more abstract event. To use their example, we want to predict that pushing a glass over a counter will result in the abstract event of “shattered glass.” We don’t need to know the precise pixel location of every shattered glass.
• The inverse model has to deal with ambiguity: there are multiple actions that may head to a resulting goal state, or perhaps no action at all can possibly lead to the next state.

All these factors require some re-thinking in terms of our model architecture (and training protocol). One obvious alternative the authors suggest is to avoid acting on image space and just feed all images into a CNN trained on ImageNet data and extract some intermediate layer. The problem is that it’s unclear if object classification and object manipulation mandate a similar set of features. One would also need to fine-tune ImageNet somehow, which would make this more task-specific (e.g., for a different workstation setup, you’d need to fine-tune again).

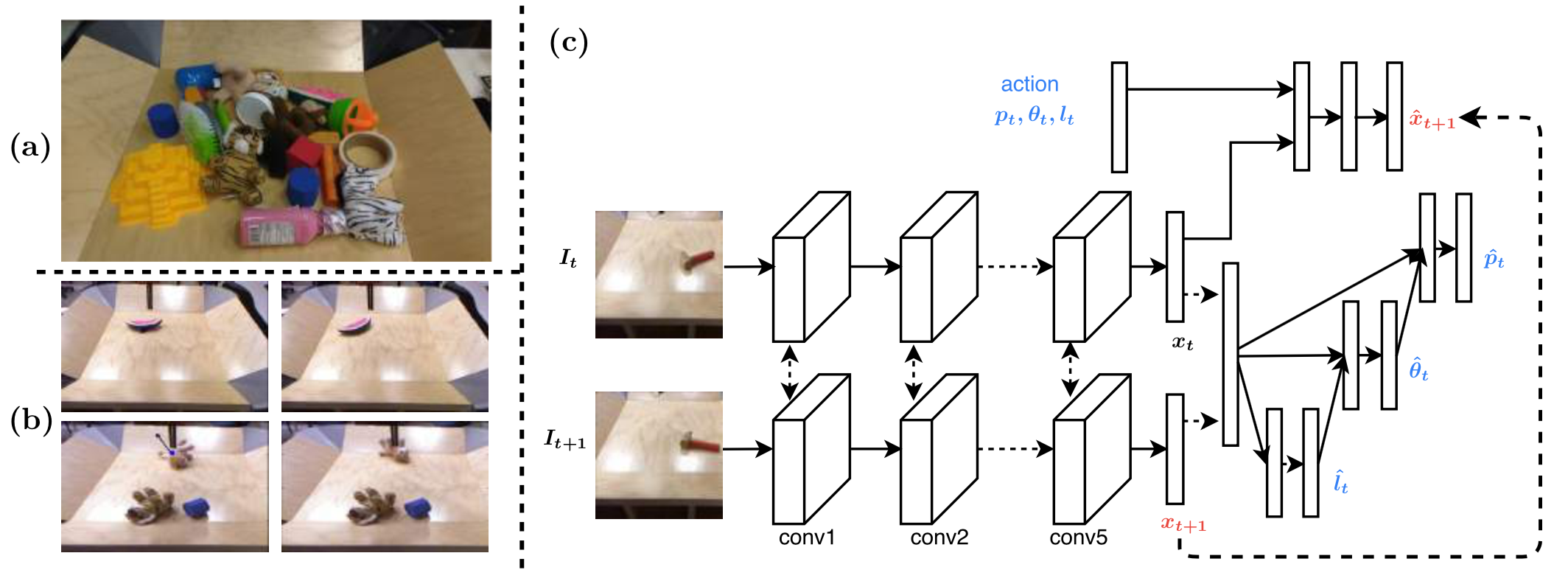
Figure from their paper describing (a) objects used, (b) before/after image pairs, (c) the network.

Their solution, shown above, involves the following:

• Two consecutive images \(I_t, I_{t+1}\) are separately passed through a CNN and then the output \(x_t, x_{t+1}\) (i.e., latent feature representation) is concatenated.

• To conclude the inverse model, \((x_t, x_{t+1})\) are used to conditionally estimate the poke length, poke angle, and then poke location. We can measure the prediction accuracy since all the relevant information was automatically collected in the training data.

  As to why we need to predict conditionally: I’m assuming it’s so that we can get “more reasonable” metrics since knowing the poke length may adjust the angle required, etc., but I’m not sure. (The project website actually shows a network which doesn’t rely on this conditioning … well OK, it’s probably not a huge factor.) Update 03/29/2018: actually, it’s probably because it reduces the number of trainable weights.

  Also, the three poke attributes are technically continuous, but the authors simply discretize.

• For the forward model, the action \((p_t, \theta_t, l_t)\) along with the latent feature representation \(x_t\) of image \(I_t\) is concatenated and fed through its own neural network, to predict \(x_{t+1}\), which in fact we already know as we have passed it through the inverse model!

By integrating both networks together, and making use of the randomly-generated training data to provide labels for both the forward and inverse model, they can simply rely on one loss function to train:

\[L_{\rm joint} = L_{\rm inv}(u_t, \hat{u}_t, W) + \lambda L_{\rm fwd}(x_{t+1}, \hat{x}_{t+1}, W)\]

where \(\lambda > 0\) is a hyperparameter. They show that using the forward model is better than ignoring it by setting \(\lambda = 0\), so that it is advantageous to simultaneously learn the task feature space and forecasting the outcome of actions.

To evaluate their model, they supply their robot with a goal image \(I_g\) and ask it to apply the necessary pokes to reach the goal from the current starting state \(I_0\). This by itself isn’t enough: what if \(I_0\) and \(I_g\) are almost exact the same? To make results more convincing, the authors:

• set \(I_0\) and \(I_g\) to be sufficiently different in terms of pixels, thus requiring a sequence of pokes.
• use novel objects not seen in the (automatically-generated) training data.
• test different styles of pokes for different objects.
• compare against a baseline of a “blob model” which uses a template-based object detector and then uses the vector difference to compute the poke.

One question I have pertains to their greedy planner. They claim they can provide the goal image \(I_g\) into the learned model, so that the greedy planner sees input \((I_t,I_g)\) to execute a poke, then sees the subsequent input \((I_{t+1},I_g)\) for the next poke, and so on. But wasn’t the learned model trained on consecutive images \((I_t,I_{t+1})\) instead of \((I_t,I_g)\) pairs?

The results are impressive, showing that the robot is successfully able to learn a variety of pokes even with this greedy planner. One possible caveat is that their blob baseline seems to be just as good (if not better due to lower variance) than the joint model when poking/pushing objects that are far apart.

Their strategy of combining networks and conducting self-supervised learning with large-scale, near-automatic data collection is increasingly common in Deep Learning and Robotics research, and I’ll keep this in mind for my current and future projects. I’ll also keep in mind their comments regarding generalization: many real and simulated robots are trained to achieve a specific goal, but they don’t really develop an underlying physics model that can generalize. This work is one step in the direction of improved generalization.

Sample efficiency is a huge problem in reinforcement learning. Popular general-purpose algorithms, such as vanilla policy gradients, are effectively performing random search in the environment¹, and may be no better than Evolution Strategies, which is more explicit about acting random (I mean, c’mon). The sample-efficiency problem is exacerbated when environments contain sparse rewards, such as when it consists of just a binary signal indicating success or failure.

To be clear, the reward signal is an integral design parameter of a reinforcement learning environment. While it’s possible to engage in reward shaping (indeed, there is a long line of literature on just this topic!) the problem is that this requires heavy domain-specific engineering. Furthermore, humans are notoriously bad at specifying even our own preferences; how do we expect us to define accurate reward functions in complicated environments? Finally, many environments are most naturally specified by the binary success signal introduced above, such as whether or not an object is inserted into the appropriate goal state.

I will now summarize two excellent papers from OpenAI (plus a few Berkeley people) that attempt to improve sample efficiency in reinforcement learning environments with sparse rewards: Hindsight Experience Replay (NIPS 2017) and Overcoming Exploration in Reinforcement Learning with Demonstrations (ICRA 2018). Both preprints were updated in February so I encourage you to check the latest versions if you haven’t already.

Hindsight Experience Replay

Hindsight Experience Replay (HER) is a simple yet effective idea to improve the signal extracted from the environment. Suppose we want our agent (a simulated robot, say) to reach a goal \(g\), which is achieved if the configuration reaches the defined goal configuration within some tolerance. For simplicity, let’s just say that \(g \in \mathcal{S}\), so the goal is a specific state in the environment.

When the robot rolls out its policy, it obtains some trajectory and reward sequence

\[(s_0, a_0, r_0, s_1, a_1, r_1, \ldots, s_{T-1}, a_{T-1}, r_{T-1}, s_{T}) \sim \pi_b, P, R\]

achieved from the current behavioral policy \(\pi_b\), internal environment dynamics \(P\), and (sparse) reward function \(R\). Clearly, in the beginning, our agent’s final state \(s_T\) will not match the goal state \(g\), so that all the rewards \(r_t\) are zero (or -1, as done in the HER paper, depending on how you define the “non-success” reward).

The key insight of HER is that during those failed trajectories, we still managed to learn something: how to get to the final state of the trajectory, even if it wasn’t what we wanted. So, why not use the actual final state \(s_T\) and treat it as if it was our goal? We can then add the transitions into the experience replay buffer, and run our usual off-policy RL algorithm such as DDPG.

In OpenAI’s recent blog post, they have a video describing their setup, and I encourage you to look at the it along with the paper website — it’s way better than what I could describe. I’ll therefore refrain from discussing additional HER algorithmic details here, apart from providing a visual which I drew to help me better understand the algorithm:

My visualization of Hindsight Experience Replay.

There are a number of experiments that demonstrate the usefulness of HER. They perform experiments on three simulated robotics environments and then on a real Fetch robot. They find that:

• DDPG with HER is vastly superior to DDPG without HER.

• HER with binary rewards works better than HER with shaped rewards (!), providing additional evidence that reward shaping may not be fruitful.

• The performance of HER depends on the sampling strategy for goals. In the example earlier, I suggested using just the last trajectory state \(s_T\) as the “fake” goal, but (I think) this would mean the transition \((s_{T-1},a_{T-1},r_{T-1},s_T)\) is the only one which contains the dense reward \(r_{T-1}\); there would still be \(T-1\) other states with the non-informative reward. There are alternative strategies, such as sampling more frequent states. However, doing this too much has a downside in that “fake” goals can distract us from our true objective.

• HER allows them to transfer a policy trained on a simulator to a real Fetch robot.

Overcoming Exploration in Reinforcement Learning with Demonstrations

This paper extends HER and benchmarks using similar environments with sparse rewards, but their key idea is that instead of trying to randomly explore with RL algorithms, we should use demonstrations from humans, which is safer and widely applicable.

The idea of combining demonstrations and supervised learning with reinforcement learning is not new, as shown in papers such as Deep Q-Learning From Demonstrations and DDPG From Demonstrations. However, they show several novel, creative ways to utilize demonstrations. Their algorithm, in a nutshell:

• Collect demonstrations beforehand. In the paper, they obtain them from humans using virtual reality, which I imagine will be increasingly available in the near future. This information is then put into a replay buffer for the demonstrator data.

• Their reinforcement learning strategy is DDPG with HER, with the basic sampling strategy (see discussion above) of only using the final state as the new goal. The DDPG+HER algorithm has its own replay buffer.

• During learning, both replay buffers are sampled to get the desired proportion of supervisor data and data collected from environment interaction.

• For the actor (i.e., policy) update in DDPG, they add the Behavior Cloning loss in addition to the normal gradient update for DDPG (function denoted as \(J\)):

  \[\lambda_1 \nabla_{\theta_\pi}J - \lambda_2 \nabla_{\theta_\pi} \left\{ \sum_{i=1}^{N_D}\|\pi(s_i|\theta_\pi ) - a_i\|_2^2 \right\}\]

  I can see why this is useful. Notice, by the way, that they are not just using the demonstrator data to initialize the policy. It’s continuously used throughout training.

• There’s one problem with the above: what if we want to improve upon the demonstrator performance? The behavior cloning loss function prevents this from happening, so instead, we can use the Q-filter, a clever contribution:

  \[L_{BC} = \sum_{i=1}^{N_D}\|\pi(s_i|\theta_\pi ) - a_i\|_2^2 \cdot \mathbb{1}_{\{Q(s_i,a_i)>Q(s_i,\pi(s_i))\}}.\]

  The critic network determines \(Q\). If the demonstrator action \(a_i\) is better than the current actor’s action \(\pi(s_i)\), then we’ll use that term in the loss function. Note that this is entirely embedded within the training procedure: as the critic network \(Q\) improves, we’ll get better at distinguishing which terms to include in the loss function!

• Lastly, they use “resets”. I initially got confused about this, but I think it’s as simple as occasionally starting episodes from within a demonstrator trajectory. This should increase the presence of relevant states and dense rewards during training.

I enjoyed reading about this algorithm. It raises important points about how best to interleave demonstrator data within a reinforcement learning procedure, and some of the concepts here (e.g., resets) can easily be combined with other algorithms.

Their experimental results are impressive, showing that with demonstrations, they outperform HER. In addition, they show that their method works on a complicated, long-horizon task such as block stacking.

Closing Thoughts

I thoroughly enjoyed both of these papers.

• They make steps towards solving relevant problems in robotics: increasing sample efficiency, dealing with sparse rewards, learning long-horizon tasks, using demonstrator data, etc.

• The algorithms are not insanely complicated and fairly easy to understand, yet seem effective.

• HER and some of the components within the “Overcoming Exploration” (OE) algorithm are modular and can easily be embedded into well-known, existing methods.

• The ablation studies appear to be done correctly for the most part, and asking for more experiments would likely be beyond the scope of a single paper.

If there are any possible downsides, it could be that:

• The HER paper had to cheat a bit on the pick-and-place environment by starting trajectories from when the gripper grips the block.

• In the OE paper, their results which benchmark against HER (see Section 6.A, 6.B) were done with only one random seed, and that’s odd given that it’s entirely in simulation.

• Their OE claim that the method “can be done on real robot” needs additional evidence. That’s a bold statement. They argue that “learning the pick-and-place task takes about 1 million timesteps, which is about 6 hours of real world interaction time” but does that mean we can really execute the robot that often in 6 hours? I’m not seeing how the times match up, but I guess they didn’t have enough space to describe this in detail.

For both papers, I was initially disappointed that there wasn’t code available. Fortunately, that has recently changed! (OK, with some caveats.) I’ll go over that in a future blog post.

---

My preprint on surgical debridement and robot calibration was accepted to the 2018 IEEE International Conference on Robotics and Automation (ICRA). It’s in Brisbane, Australia, which means I’ll be going to Australia for the second time in less than a year — last August, I went to Sydney for UAI 2017.

I’m excited about this opportunity and look forward to traveling to Brisbane in May. (That is, assuming Berkeley’s Disabled Students’ Program isn’t as slow as they were in August, but never mind.) I have already booked my travel reservations and registered for the conference.

Everyone knows that long-haul international travel is expensive, but what might not be clear to those outside academia is that conference registration fees can be just as high as those airfare fees. For ICRA, the cost of my registration came to be 1,171.36 AUD before taxes, and 1,275.00 AUD with taxes. That corresponds to 1,033.94 in US dollars. Ouch.

Fortunately, I’m going to get reimbursed, since Berkeley professors are not short on money, but I still wish that costs could be lower. The breakdown was: 31.36 AUD for a hotel deposit (I’ll pay the full hotel fees when I arrive in May), 600 AUD for the early-bird IEEE student membership registration, 100 AUD for the workshops/tutorials, and 440 AUD for the two extra page charge.

Wait, what was the last one?

Ah, I should clarify. The policy of ICRA, and for many IEEE conferences at that (hence the title of this blog post), is the following:

Papers to ICRA can be submitted through two channels:

1. To ICRA. Six pages in standard ICRA format and a maximum of two additional pages can be purchased.
2. To the IEEE Robotics and Automation Letters (RA-L) journal, and tick the option for presentation at ICRA. Six pages in standard ICRA format are allowed for each paper, including figures and references, but a maximum of two additional pages can be purchased. Details are provided on the RA-L webpage and FAQ.

All papers are submitted in PDF format and the page count is inclusive of figures and references. We strongly encourage authors to submit a video clip to complement the submission. Papers hosted on arXiv may be submitted to ICRA.

So, in short, we can have six pages, and can purchase two extra pages if needed.

This makes no sense.

Is it because of printing costs associated with the proceedings? It shouldn’t be. The proceedings, as far as I know, are those enormous books that concatenate all the papers from a conference.

They are also worthless and should never be printed outside of maybe one or two historical copies for IEEE’s book archives. No one should read directly from them. Who has the time? Academics are judged based on the papers they produce, not the papers they consume. This year, ICRA alone accepted 1030 papers (!!). Yes, over a thousand. It makes no sense to browse proceedings to search for a paper; just type in a search query on Google Scholar. If you think you might be missing a gem somewhere in the proceedings, I wouldn’t worry. Good papers will make themselves known eventually through word of mouth. They also tend to be widely accessible to all, such as being available on arXiv rather than being stuck behind an IEEE paywall. Most universities have IEEE subscriptions so it’s not generally a problem to download IEEE papers for free, but it’s still a bit of an unnecessary nuisance.

Speaking of arXiv, perhaps IEEE doesn’t follow a similar model due to hosting costs? That doesn’t seem like a good rationale, and in particular it doesn’t justify the steep jump in price from 6 to 8 pages. Why not have pages 1 through 6 charged accordingly? Or simply make the charge based on file size instead of page size, while obviously keeping a hard page limit to alleviate the load on reviewers. There seem to be way more rational price structures than the 220 AUD each for pages 7 and 8.

It seems like ICRA organizers would prefer to see 6 page papers, yet the problem is that everyone knows that if you allow 8 pages, then that becomes the effective lower bound on paper length. An 8-page paper has a better chance of being accepted to ICRA than a 7-page paper, which in turn has odds over a 6-page paper. And so on. Indeed, if you look at ICRA papers nowadays, the vast majority hit the 8 page limit, many with barely a line to spare (such as my paper!). The trend is possibly even more pronounced with ICML, NIPS, and other AI conferences, from my anecdotal experience reading those papers.

Such a cost structure might needlessly disadvantage students and authors from schools without the money to easily pay the over-length fees. This is further exacerbated by ICRA’s single-blind policy, where reviewers can see the names of authors and thus be influenced by research fame and school institution name.

In short, I’m not a fan of the two-page extra charge, and I would suggest that ICRA (and similar IEEE-based conferences) switch to a simple, hard, 8-page limit for papers. In addition, I would also like to see all accepted papers freely available for download in an arXiv-style format. If hosting costs are a burden, a more rational price structure would be to slightly increase the conference registration fees, or encourage authors to upload their papers on arXiv in lieu of being hosted by ICRA.

To be clear, I’m still extremely excited about attending ICRA, and I’m grateful to IEEE for organizing what I’ve heard is the preeminent conference on robotics. I just wish that they were a little bit clearer on why they have this two-page extra charge policy.

In this post, I build upon my previous one by further investigating fundamental concepts in Murray, Li, and Sastry’s A Mathematical Introduction to Robotic Manipulation. One of the challenges of their book is that there’s a lot of notation, so I first list the important bits here. I then review an example that uses some of this notation to better understand the meaning of twists and exponential coordinates.

Side comment: there is an alternative, more recent robotics book by Frank C. Park and Kevin M. Lynch called Modern Robotics. It’s available online and has its own Wikipedia, and even has some lecture videos! Despite its 2017 publication date, the concepts it describes are very similar to Murray, Li, and Sastry, except that the presentation can be a bit smoother. The notation they use is similar, but with a few exceptions, so be aware of that if you’re reading their book.

Back to our target textbook. Here is relevant notation from Murray, Li, and Sastry:

• The unit vector \(\omega \in \mathbb{R}^3\) specifies a direction of rotation, and \(\theta \in \mathbb{R}\) represents the angle of rotation (in radians).

  An important fact is that any rotation can be represented as rotating by some amount through an axis vector, so we could write rotation matrices \(R\) as functions of \(w\) and \(\theta\), i.e., \(R(\omega, \theta)\). Murray, Li, and Sastry call this “Euler’s Theorem”.

  Note: if you’re familiar with the Product of Exponentials formula, then \(\theta = (\theta_1, \ldots, \theta_J)\), which generalizes to the case when there are \(J\) joints in a robotic arm. Also, \(\theta_i\) doesn’t have to be an angle; it could be a displacement, which would be the case if we had a prismatic joint.

• The cross product matrix \(\hat{\omega}\) satisfies \(\hat{\omega} p = \omega \times p\) for some \(p \in \mathbb{R}^3\), where \(\theta\) indicates the cross product operation. More formally, we have

  \[\hat{\omega} = \begin{bmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{bmatrix}\]

  and so \(\hat{\omega}\) is a skew-symmetric matrix, of which the set of those is denoted as \(so(3)\). This is easily verified by explicit computation.

• The matrix exponential \(e^{\hat{\omega} \theta}\) is a \(3\times 3\) matrix in the set \(SO(3)\). In other words, it’s a rotation matrix! We can write it in closed form from Rodrigues’ formula:

  \[e^{\hat{\omega} \theta} = I + \hat{\omega} \sin \theta + \hat{\omega}^2 (1- \cos \theta)\]

  Here’s the relevant mathematical relationship: the exponential map transforms skew-symmetric matrices into orthogonal matrices, and every rotation matrix can be represented as the matrix exponential of some skew-symmetric matrix.

• A twist \(\hat{\xi} \in se(3)\) is defined as the set of \(4\times 4\) matrices parameterized by exponential coordinates \(\xi = (v,\omega)\) s.t. \(v \in \mathbb{R}^3\) and \(\hat{\omega} \in so(3)\). The matrix is written as

  \[\hat{\xi} = \begin{bmatrix} \hat{\omega} & v \\ 0 & 0 \end{bmatrix}\]

  and yes, the last row consists of four zeros. We can derive this matrix from considering rotations about revolute and prismatic joints, where \(\omega\) is the axis of rotation, and \(v\) is the vector describing the translation. (See Section 3.2 in Murry, Li, and Sastry for details.)

  Incidentally, sometimes we call twists as \(\hat{\xi}\theta\), or with the \(\theta\) “attached” to it. We can also do the same for the exponential coordinates.

• The matrix exponential of a twist \(e^{\hat{\xi}\theta}\) represents the relative motion of a rigid body. Hence, if we left-multiply this with a vector, we interpret it as moving the input vector with respect to the same frame. Said another way, we are not changing the “frame of reference” for the input vector.

  Given twist coordinates \((v,\omega)\), we can explicitly construct the RBMs:

  \[e^{\hat{\xi}\theta} = \begin{bmatrix} I & v\theta \\ 0 & 1 \end{bmatrix}\]

  if \(\omega = 0\). This is equivalent to a pure translation. If \(\omega \ne 0\), we have the slightly more complicated formula

  \[e^{\hat{\xi}\theta} = \begin{bmatrix} e^{\hat{\omega}\theta} & (I-e^{\hat{\omega}\theta})(\omega \times v) + \omega \omega^T v \theta \\ 0 & 1 \end{bmatrix} .\]

  Both of the above are elements of \(SE(3)\), so they are rigid body motions. To be clear, you need to construct these from the actual definition of a matrix exponential based on its Taylor series expansion.

Let’s look at the example in the figure below to better understand the above concepts.

We have inertial frame \(A\) and body frame \(B\). With some pencil and paper, you can show that the RBM from \(B\) to \(A\) is:

\[g_{ab} = \begin{bmatrix} R_{ab} & p_{ab} \\ 0& 1 \end{bmatrix} = \begin{bmatrix} \cos \alpha & -\sin \alpha & 0 & -l_2 \sin \alpha \\ \sin \alpha & \cos \alpha & 0 & l_1 + l_2 \cos \alpha \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\]

which follows the style from my last post: determine the rotation and translation components and then plug them in. Fortunately, the rotation is about the \(z\) axis, so \(R_{ab}\) is easy.

It turns out that every RBM can be expressed as the exponential of some twist \(\xi \in \mathbb{R}^6\). So let’s consider the following:

Given that \(g_{ab} = e^{\hat{\xi} \theta}\) (note \(\hat{\xi}\), not \(\xi\)) and that we know the exact form of \(g_{ab}\), can we compute \(\xi\)?

To do this, we need to compute the components \(v\) and \(\omega\).

• Let’s do \(\omega\) first. From our above equations for \(e^{\hat{\xi}\theta}\) and \(g_{ab}\), we equate components and see that we need

  \[e^{\hat{\omega}\theta} = R_{ab}\]

  We know \(R_{ab}\) corresponds to a rotation matrix about the \(z\)-axis only. This means \(\omega = (0,0,1)\). We also simply set \(\alpha = \theta\).

• Now consider \(v\). Once again, we equate components from both sides to get

  \[p_{ab} = \begin{bmatrix} (I-e^{\hat{\omega}\theta})(\omega \times v) + \omega \omega^T v \theta \end{bmatrix} = \begin{bmatrix} (I-e^{\hat{\omega}\theta})\hat{\omega} + \omega \omega^T \theta \end{bmatrix} v\]

  This is the standard “solve for \(x\) in \(Ax=b\)” problem that you saw in linear algebra classes. Solving for \(v\), we get \(v = (\frac{l_1-l_2}{2}, \frac{(l_1+l_2)\sin\alpha}{2(1-\cos\alpha)}, 0)\).

We conclude that our exponential coordinates which generated \(g_{ab}\) are

\[\xi = \begin{bmatrix} \frac{l_1-l_2}{2} \\ \frac{(l_1+l_2)\sin\alpha}{2(1-\cos\alpha)} \\ 0\\ 0\\ 0\\ 1 \end{bmatrix}\]

assuming that \(\alpha \ne 0\)

Over the last few weeks, I have been devouring Murray, Li, and Sastry’s A Mathematical Introduction to Robotic Manipulation. It’s freely available online and, despite the 1994 publication date, is still relevant for robotic manipulation as it’s used in EE206 at Berkeley.

(The main novelty today, from my perspective, is the use of Deep Learning to automate out analytic models under certain conditions, but I still think it’s valuable for me to know classical robotics concepts.)

In this post, I discuss the Special Exponential group, denoted as \(SE(3)\). We can define it as follows:

\[SE(3) := \{(p,R) \mid p \in \mathbb{R}^3, R \in SO(3) \}\]

where \(p\) is a position vector, and \(R\) is a matrix in the special orthogonal group \(SO(3)\):

\[SO(3) := \{R \mid R \in \mathbb{R}^{3\times 3}, R^TR=I_{3}, {\rm det}(R)=+1\}\]

This is the same as saying that \(R\) is a rotation matrix.

Side comment: the reason for “\((3)\)” as the input is that \(SE\) and \(SO\) can be generalized to an arbitrary amount of dimensions. However, I’m only concerned about robotic manipulation in \(\mathbb{R}^3\).

The above suggests the obvious question:

For what purpose do we utilize \(SE(3)\)?

We use \(SE(3)\) to encode rigid body motions (RBMs) in robotic manipulation, which preserve distance between points and angles between vectors. RBMs consist of a rotation and a translation. To visualize RBMs, look at the left of the figure below. There are two coordinate frames: frame \(A\), which is “inertial” (I think of this as the “default” frame), and frame \(B\), attached to the base of the curvy object drawn there.

Vector \(p_{ab} \in \mathbb{R}^3\) shows the 3-D position of the origin of \(B\) with respect to \(A\). This ordering from \(B\) to \(A\) and not vice versa is important, and it’s important to know these well for robotic manipulation, which in advanced contexts relies on multiple, consecutive coordinate frames attached to links in a robot arm. For rotation matrices, we’ll keep the ordering of subscripts the same and write \(R_{ab}\) to indicate that it transforms 3-D points from frame \(B\) to frame \(A\).

Left: visualization of two coordinate frames, one inertial and one attached to the base of an object. Right: again, two coordinate frames visualized, this time in the context of rotating about an axis.

Now consider the point \(q\) on the object. We can express its coordinates as \(q_a\) or \(q_b\), depending on which frame of \(A\) or \(B\) is our reference. Suppose we have \(q_b\). A rigid body motion can be conducted as follows:

\[q_a = p_{ab} + R_{ab}q_b\]

and we’ll collect as \(g_{ab} = (p_{ab},R_{ab})\) all the information needed to specify an RBM, transforming coordinates from \(B\) to \(A\). This is an element of \(SE(3)\). Indeed, any such RBM must be an element of \(SE(3)\), which defines what’s known as a configuration space of RBMs. Configuration spaces are defined in page 25 of Murray et al:

More generally, we shall call a set \(Q\) a configuration space for a system if every element \(x\in Q\) corresponds to a valid configuration of the system and each configuration of the system can be identified with a unique element of \(Q\).

I should also provide some intuition to make it clear what happens when we “transform coordinates.” One way is as follows. If we view \(p_{ab}\) as jetting out in the positive \(x\), \(y\), and \(z\) directions of frame \(A\), and the same for \(q_b\) w.r.t. frame \(B\), then the components of \(q_a\) are element-wise larger than in \(q_b\). This is why we add when doing RBMs with translations, since the vector \(p_{ab}\) will increase the values. (Drawing a picture really helps.)

Keeping \(p_{ab}\) and \(R_{ab}\) separate can result in some cumbersome math when a bunch of rotations and translations are combined. Thus, it’s common to use homogeneous coordinates. A full discussion is beyond the scope of this blog post, but for us, the important point is that if \((p,R) \in SE(3)\), then the equivalent homogeneous representation is

\[\begin{bmatrix} R & p \\ 0 & 1 \end{bmatrix} \in \mathbb{R}^{4\times 4}\]

where the “0” above is a row vector of three zeros. This enables us to perform one matrix-vector multiply for a 3-D point which is expanded with a fourth coordinate with a “1” in it. Thus, the origin point is \(o = (0,0,0,1)^T\), and for vectors — defined as the difference between two points — the fourth component is zero.

Let’s do an example. Consider the second image in the figure above, showing rotation about an axis \(\theta\). Given a fixed, “real-life”, physical point, let’s show how to encode a rigid body transformation which can transform a coordinate representation of that point from frames \(B\) to \(A\).

• Translation. Inertial frame \(A\) and frame \(B\) differ only by \(l_1\) in the y-direction, with \(p_{ab} = (0,l_1,0)^T\) representing the origin of frame \(B\) with respect to frame \(A\).

• Rotation. The rotation about \(\theta\) coincides with the \(z\) axis. Hence, we use the well-known formula for the \(z\)-axis rotation matrix:

  \[R_z(\theta) = \begin{bmatrix} \cos \theta & - \sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}\]

  While the precise positioning of the sines and cosines might not be immediately apparent, it should be clear why the last row looks like that, since a rotation about the \(z\) axis leaves the \(z\) component of the 3-D vector unchanged. You can also easily check that \(R^TR=I_3\).

  The matrix above is \(R_{ab}\), the orientation of the origin of frame \(B\) w.r.t. frame \(A\).

These two form our specification in \(SE(3)\). Combining these by using the homogeneous representation for compactness, our RBM from \(B\) to \(A\) is:

\[\underbrace{\begin{bmatrix} a_x \\ a_y \\ a_z \\ 1 \end{bmatrix}}_{\vec{a}} = \begin{bmatrix} \cos \theta & - \sin \theta & 0 & 0 \\ \sin \theta & \cos \theta & 0 & l_1\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \underbrace{\begin{bmatrix} b_x \\ b_y \\ b_z \\ 1 \end{bmatrix}}_{\vec{b}}\]

where \(\vec{a}\) and \(\vec{b}\) represent, in homogeneous coordinates, the same physical point but with respect to frames \(A\) and \(B\), respectively.

[Warning: long read]

A year ago, I listed all the books that I read in the year 2016. I listed 35 books with summaries for each, and grouped them into categories by subject. I’m pleased to announce that I am continuing my tradition with this current blog post, which summarizes all the books I read in 2017.

As before, I am only listing non-fiction books, and am excluding (among other things) textbooks, magazines, and certainly all the academic papers¹ that I read. Books with starred titles (like ** this **) are those that I especially enjoyed reading, for one reason or another.

In 2017, I read 43 books, which is eight more than the 35 I reported on last year. Yay! The book categories are:

1. Artificial Intelligence and Robotics (11 Books)
2. Technology, Excluding AI/Robotics (5 Books)
3. Business and Economics (5 Books)
4. Biographies and Memoirs (6 Books)
5. Conservative Politics (3 Books)
6. Self-Help and Personal Development (3 Books)
7. Psychology and Human Relationships (4 Books)
8. Miscellaneous (6 Books)

Within each section, books are listed according to publication date.

I hope you enjoy this blog post! For 2018, I hope to continue reading lots and lots of non-fiction books with a heavy focus on technology, businesses, and economics. For the full set of these “reading list” posts, see this page.

Group 1: Artificial Intelligence and Robotics

Yowza! From the 11 books here, you can tell that I’m becoming a huge fan of this genre. ;-)

• ** Incognito: The Secret Lives of the Brain ** is a thrilling 2011 book by neuroscientist David Eagleman of the Baylor College School of Medicine. (I consider this book as “AI” in this blog post, though you could argue that “Psychology” might be better.) It is clearly designed for the lay reader with interest in neuroscience, like me, due to a number of engaging examples that thrill the reader without going overboard with the technical content. Eagleman describes how we don’t actually have that much control over our brain, that there are so many unexpected contradictions with how we think, and mentions a few interesting neuroscience factoids. Did you know, for instance, that half of a child’s brain can be removed and the child can still survive? On a technical note, I was impressed with how Eagleman referenced a few machine learning papers from Michael I. Jordan and Geoff Hinton in his footnotes about hierarchical learning. From the perspective of a computer scientist, the most interesting part was when he talked about the brain being a team of competing rivals. This is awfully similar to the idea behind Generative Adversarial Networks an enormously successful and well-cited paper that came out in NIPS 2014 … three years after this book was published! I have no idea how a non-computer scientist was able to almost predict this, but it shows that cross-collaboration between neuroscientists may be good for AI. He doesn’t get everything right, though. He mentions more than once that artificial neural networks have been a failure. Well… this book was published in 2011, and Alex-Net came out in 2012, so that kind of flopped quickly. Despite this, I hope to see Eaglemen write another book about the brain so that I can see a revised perspective. Incognito also contains interesting perspectives on neuroscience and the law. Eagleman doesn’t take sides but doesn’t go in too much depth either. He says the “bar” for blameworthiness will change depending on available neuroscience, which he says is a mistake (and I agree).

• ** The Most Human Human: What Artificial Intelligence Teaches Us About Being Alive ** is an engaging 2011 book written by Brian Christian, who also (co-)authored another book I read this year, Algorithms to Live By. This book’s main focus is on the Turing Test, and it plays a greater theme in this one more than any of the other AI books I’ve read. Simply put, while we’re so obsessed about getting a computer to fool human judges (the “most human computer”), Christian argues that an equally important criteria is the “most human human.” In other words, in the Turing Test, who is the human that can most convince the judges that he/she is human? The book’s chapters are explorations of the different factors that make us human, among other things our ability to barge and interrupt, our use of “um” and “uh”, our constant sidetracking, and so forth. Intuitively, these are hard for a computer to model. Christian has a computer science background, so some of the book covers technical concepts such as entropy, which he argues we need to be making as high as possible; low entropy means we’re not saying anything worth knowing more about. And yet, these seem to be the most negatively encouraged aspects of our society, which is quite odd in Christian’s opinion. I enjoyed reading most of the book because it stated observations that seem obvious to me in retrospect, but which I never gave much thought. That’s the best kind of observation. (It’s like Incognito to some extent, and indeed the Incognito author praises this book!) The biggest drawback is that it never goes through a blow by blow of the actual Turing test! I mean, c’mon, I was looking forward to that, and Christian essentially ruined it by fast forwarding to the end, when he mentions he won the title of the “most human human.” Well, congratulations dude, but why wasn’t there at least a complete transcript in the book???

• ** Our Final Invention: Artificial Intelligence and the End of the Human Era ** is a 2013 book by documentary filmmaker James Barrat exploring the rise of AI and its potential existentialist risk. This is not far off the mainstream of AI researchers and programmers as it sounds. In fact, Peter Norvig and Stuart Russell include a brief discussion about it at the end of their famous AI textbook. Russell has also explicitly said that he’s clearly worried about superintelligence. So what is superintelligence? I view it as AI that is so far advanced that it becomes better and better, and surpasses humans in just about every quality imaginable.² I think I enjoyed reading this book, even if it is a tad too sensational. There isn’t that much technical detail, which is OK since it’s a popular science book. Barrat makes an excellent point that scientists need to make their work accessible to the public. I agree — that’s partly why I discuss technical stuff on this blog — but I also think that people have got to start learning more math on their own. It needs to be a two-way partnership. Moving on, an unexpected benefit of reading Our Final Invention was that I learned about the work done by I.J. Good, Eliezer Yudowsky, and others from the Machine Intelligent Research Institute. I’m embarrassed to admit that I didn’t know about those two people beforehand, but now I will remember their names. Unlike MIRI in most Berkeley AI research groups, such as the ones I’m in, we don’t give a modicum of thought to existential risks of AI, but the topic is garnering more attention. One final comment about the book: Barrat mentions that no computer is better than a child at object recognition. Well, whoops. They are now! He talks a lot about neural networks and how we don’t understand them, which by now feels old and I wish authors would take note of all the people workong on this area. I’d like to see an updated version of Our Final Invention in 2018, with the last five years of AI advancement taken into consideration.

• ** Superintelligence: Paths, Dangers, Strategies ** is a 2014 book by Oxford philosopher Nick Bostrom.³ His philosophy background is apparent in the way Superintelligence is written, though it is obviously much easier to read than a real, academic philosophy paper. In this book, Bostrom considers when AI grows to the point where machines are “superintelligent.” That term can be broadly understood as when machines are so powerful and intelligent that they effectively have complete control over the future of the universe. Why, Bostrom says, can we assume that superintelligence is friendly? We cannot, he concludes. The book is about different ways we can get to superintelligence (i.e., “paths”) including AI, emulating the brain, collective superintelligence (think a super-charged Internet) and so forth. There are also “dangers” and “strategies”. Bostrom convincingly explains why superintelligence poses an existential risk to humanity, and also explains what strategies we may take to counter it, such as by uploading appropriate values to the agent. Unfortunately, none of his solutions are clear-cut. There are two things you will notice when reading this book. First, almost every assumption has a counterexample or unexpected consequence. Bostrom often comes up contrived scenarios for this purpose. Second, Bostrom frequently cites Eliezer Yudkowsky’s work. I first learned about Yudkowski by reading James Barrat’s Our Final Invention (see above). If you like Yudkowsky, you’ll like Bostrom. Taking a more general view, Superintelligence is meant to be a serious academic-style discussion, but not a recipe that can be easily followed, because it assumes so many things and continues to make the reader feel like every case is hopelessly complicated with advantages and disadvantages abound, both obvious and non-obvious. Overall, I’m happy I read this book even if it is wildly premature. It made me think hard about any assumptions I make in my work.

• What to Think About Machines That Think: Today’s Leading Thinkers on the Age of Machine Intelligence collects responses based on a 2015 survey of the EDGE question: “what do you think about machines that think?” This was sent to about a hundred or so experts in a variety of fields, mostly different academics and well-known authors. Obvious inclusions were Nick Bostrom (of Superintelligence fame), Eliezer Yudkowsky, Stuart Russell, Peter Norvig, and others, but there were also some interesting new additions. I of course did not know the vast majority of the people here. This book is a bit of an unusual format; each author’s answer to this question took up 1-4 pages. There were no constraints otherwise, so the answers varied considerably. For instance, I like Steven Pinker’s comment of why people don’t think AI will “naturally develop along female lines […] without the desire to take over the world.” Gee, isn’t that stereotyping, Pinker?? There were also some amusing responses, such as when someone said that he himself was an AI and people didn’t know it (!!) as well as alarmingly short answers saying “machines can’t think”. Most responses were along the same theme of: “AIs taking over the world aren’t going to happen anytime soon, but they are affecting us now, sometimes in subtle ways, and [insert ‘novel’ insight here].” Overall, while I like the idea of the book format, I think the utility that I derive from reading is more about understanding a long, engrossing story. This is not necessarily a bad book, and I can see it being useful for someone who can only read books in short 3-5 minute spurts at a time, but it’s not my style.

• ** Machines of Loving Grace: The Quest for Common Ground Between Humans and Robots **, is a 2015 book by NY Times journalist John Markoff. Though a journalist, Markoff has frequently written about AI-related topics and has good connections in the field. Machines of Loving Grace gives an impressively balanced view of the history of Artificial Intelligence (AI) and Intelligence Augmentation (IA), which can be roughly thought of as HCI (I might view it as a subset of HCI). Obviously, I am more interested in the AI aspect. Markoff covers topics such as self-driving cars (unsurprisingly), and Rodney Brooks’ Baxter robot, which has been used in many research papers that I’ve read. But more surprising from a Berkeley perspective, Markoff also mentioned Pieter Abbeel’s work, though this was his clothes folding experiment, and not his later, more exciting DeepRL stuff from 2014 and onwards. I was also — unsurprisingly — interested in Markoff’s description of the history of how the neural network pioneers met each other (e.g., Terence Sejnowski, Geoffrey Hinton, and Yann LeCun). For the IA side, the most prominent example is Apple’s Siri, which interacts with humans, though I don’t have much to say about it because I have never used Siri. Yes, I’m embarrassed. On the AI vs IA dilemma, Markoff notes people such as John McCarthy and Doug Engelbart on opposite sides. And of course who could forget Marvin Minsky who decimated the field of neural networks with his legendary 1969 book? I decided to read this based on Professor Ken Goldberg’s brief Nature article, and was pleased that I did so, mostly (again) to learn about history (since I’m trying to become like one of those AI experts…) and the importance of ensuring that, at least for AI applied to the real world, we keep the human interaction aspect in mind.

• Rise of the Robots: Technology and the Threat of a Jobless Future is a 2015 book by technologist Martin Ford, who warns that our society is not prepared to handle all the future technological advances with robots automating out jobs. He begins by arguing that IT advances have not been as useful as electricity and other breakthroughs, and indeed that is a key theme from Robert Gordon’s The Rise and Fall of American Growth. To make the point clear, in response to Ray Kurzwiel saying that smartphones have provided incalculably large benefits to their owners, Ford counters with: “in practice, they may offer little more than the ability to play Angry Birds while standing in an unemployment line.” Ford continues by citing sources and reasons for the decline of the middle class in America. This part of the book is not controversial. Ford then raises the point that the IT revolution, along with not just robotics but also machine learning, means that even “high-skilled” jobs are at risk of being automated out. We now have machines that can write as well as most humans, that play Jeopardy! (as expected, IBM’s Watson was mentioned) and which perform better at image recognition and language translation using Deep Learning. Ford worries that, in the worst case, an elite few with all the wealth will hoard it and be guarded in a fortress by robots. Yes, he admits this is science fiction (and he discusses the Singularity, probably not the best idea…) but the point seems clear. Ford concludes the book with what he probably wanted to discuss all along: Universal Basic Income to the rescue! I heard about this book from Professor Ken Goldberg’s brief Nature article, who is critical of Ford “falling for the singularity hype” and his “extremely sketchy” evidence. I probably don’t find it as bad, and lately I’ve been thinking more seriously about supporting a Universal Basic Income. We might as well try on smaller scales, given that the best we can hope for in the future is more debt and safety net cuts with Republicans (now) or more debt inefficient bureaucracy with Democrats (in 2018/2020).

• Our Robots, Ourselves: Robotics and the Myths of Autonomy, a 2015 book written by MIT professor David A. Mindell, is the third robotics-related book that I read based off of Professor Ken Goldberg’s brief Nature article. Mindell has an unusual background, being a Professor of Aeronautics and Professor of the History of Engineering and Manufacturing (I didn’t even know that was a department). He’s also a pilot. So this book brings together his expertise when he discusses what it means for robots to be automated. Our Robots, Ourselves discusses five realms: sea, land, air, war, and space, and shows that in all of those, it is not straightforward to claim that robots are being more and more autonomous at the expense of the human aspect. In addition, Mindell tells stories of the natural conflict between increasing automation and human employees. For instance, with sea, what does it mean for geologists and scuba-diving analysts if robots do it for them? Does it detract from their job? A similar thing rings true for pilots. We need some way of humans taking over in emergencies, and pilots are worried that increasing automation will lower the prerequisite skills for the job and/or reduce the job’s purpose. Next, consider war. People who once fought on the front lines or as air force pilots are feeling resentful that those who manage drones remotely are getting respect and various honors. Mindell argues that increasing automation must also go along with better human-robot interaction, a topic which is rightfully becoming increasingly important for academia and the world. After reading this book, I now believe I do not want systems to be fully autonomous (a huge issue with self-driving cars) but instead, I want the automation to work well with humans. That’s the key insight I got from this book.

• ** Algorithms to Live By: The Computer Science of Human Decisions ** is a 2016 book co-authored by writer Brian Christian and Berkeley psychology professor Tom Griffiths. It consists of 11 chapters, each of which correspond to one broad theme in computer science, such as Bayes’ Rule, Overfitting, and Caching. Most of these topics are related to algorithms and machine learning, which wasn’t particularly surprised to me given the authors’ backgrounds. I also know Professor Griffiths publishes machine learning papers on occasion, such as his groundbreaking 2004 paper Finding Scientific Topics. Algorithms to Live By lists how the major technical issues and questions related to these topics can have implications for actions in our own lives, such as dating, parking cars, and designing our rooms/desks (this example with caching always comes up). The authors point out how, in practice, the algorithms people engage in for these activities can be surprisingly correct or well off the mark of optimality, where here the metric is based on mathematical proofs. Of course, whenever we talk about mathematical proofs, we have to be clear on what assumptions we make, which will drastically affect our options, and which in fact can often validate some of the seemingly irrational activities that humans perform. I tremendously enjoyed reading this, though admittedly it was easier for me to digest the material given that I knew the main idea of the computer science concepts covered. It was nice to get a high-level overview, though, and I still learned a lot from the book since I have not studied every computer science subfield in detail. My final thought is that, just like when I read The Checklist Manifesto last year and tried to think about utilizing checklists myself, I will try and see if I can incorporate some of the authors’ suggestions in my own life.

• ** Thinking Machines: The Quest for Artificial Intelligence and Where It’s Taking Us Next ** is a recent 2017 book by journalist Luke Dormehl. I found out about it by reading Ray Kurzweil’s favorable book review in The New York Times. Kurzweil remarks that Luke is a journalist who “actually knows the technical details.” I think that’s true, though there is virtually no math in this book, or at least very little of it compared to Pedro Domingos’ book. In Thinking Machines, Dormehl mentions the backpropagation algorithm which has powered Deep Learning, but only at a very high level (obviously). He also talks about Deep Learning’s history, which I know already (and it could have been derived right from Stanford’s CS 231n slides) but it’s good to have here. Dormehl writes about the by-now famous story that “neural networks were ignored for a while then they became popular and are now known as Deep Learning,” which Professor Jitendra Malik would remark is “more marketable.” As far as technical material goes, it’s correct, so no worries. Dormehl includes a substantial amount of material about sensors, the Internet of Things (similar to Thomas L. Friedman’s Thank You For Being Late) and of course about AI ethics, laws, and the singularity. These are not new themes, but the difference between this book and others is that it’s very recent and current, which is useful due to the fast-growing pace of AI, so it was able to cover AlphaGo from DeepMind. I consider it a broad “story” about AI, and less opinionated compared to James Barrat’s Our Final Invention. It’s of reasonable length (not too long, not too short) and great for a wide audience of readers. Overall, I enjoyed reading the book, and it kept me up late longer than I should have.

• ** Heart of the Machine: Our Future in a World of Artificial Emotional Intelligence ** is a 2017 book also recommended by Ray Kurzweil. The author is Richard Yonck, founder and president of Intelligent Future Computing, a company which provides advice on the impact of technology on business and society (is this called “consulting”?). Heart of the Machine, like many AI-related books, discusses recent research and commercial advances, but it emphasizes an emotional perspective. It discusses how we got to affective computing and the rise of emotional machines. The first part contains a little history and discusses some of the labs that are working on this (e.g., the MIT Media Lab). The second, like the first, shows how many companies are measuring emotions, in part using advances in AI and Big Data analysis, and cautions us about the uncanny valley. The third part of the book is about the future, and obviously sexbots play a role. What I remember most form the book are its anecdotes, one of the most touching of which was when someone wanted to marry a robot, and a parent opposed this. Will this be the future of marriage? The first step is interracial marriage, then the next is same-sex marriage, and the last (?) step is human-machine marriage. Yonck shows his academic side by citing some ACM/IEEE International Conference on Human-Robot Interaction papers. That’s a niche-style conference but will likely grow into something much larger in the coming years (see the 2018 website here), similar to how NIPS grew from a niche into an enormous conference with thousands of attendees each year. Finally, I appreciated that Yonck said we are already merging with technology in some ways. For instance, many deaf people opt for cochlear implants to better interact in a hearing world. (I likely would have one had I been born a few years later and if hearing aids were not already highly successful for me.) We already merge with technology so much, and this is likely to increase in the future.

Group 2: Technology, Excluding AI/Robotics

These are books loosely related to technology, though excluding AI and robotics, as I discussed those in the previous section.

• ** The Second Machine Age: Work, Progress, and Prosperity in a Time of Brilliant Technologies **, co-authored by Erik Brynjolfsson and Andrew McAfee. Both authors are from MIT: Brynjolfsson is a professor of management and McAfee a research scientist. The authors appear to take the opposite perspective of economist Robert Gordon (author of The Rise and Fall of American Growth, which I discuss later), a point that they emphasize repeatedly: they argue that we are now at an inflection point and that we are on our way towards better times, and not stagnation. Their key rebuttal to Gordon is that innovation is due to recombination. Sure, we may not invent brand new things like electricity, but the IT revolution was all about combining stuff that had previously existed, and that will continue onwards as more people are able to try new things. As expected, they provide the usual disclaimers (at least from the technologically elite) that technological growth isn’t always great, that people fall behind, etc. To their credit, both men propose solutions, which I think are reasonable and — crucially in today’s politics — are widely agreed upon by economists across the entire political spectrum. For instance, they mention the universal basic income but seem to prefer the more mainstream “earned income tax credit” idea, and I think I can agree. One major quibble I have is that the book has one chapter to AI, but the actual AI portion of it is only two and a half pages long. And this for what might be the biggest technology advance of the 21st century! Fortunately, they seem to have given it greater attention since the book was first published. I bought The Second Machine Age in December 2016 as a Christmas gift, and they included a new introduction saying that they had underestimated progress in AI, particularly with deep neural networks, a topic which I frequently blog about here! (Incidentally, I saw Brynjofsson’s praise for a MOOC on Deep Learning … even MIT professors are going to MOOCs⁴ to learn about the subject!) The book is relatively straightforward to read and oozes more excitement compared to Gordon’s book. There is a book website for more details if you are interested. Brynjofsson and McAfee have since written more about Deep Learning, as you can see from their NY Times article after AlphaGo famously beat Go super-duper star Lee Sodol. I feel extremely fortunate to be in a position where, though I’m not the one creating this stuff, I can understand it.

• ** How Google Works ** is a 2014 book (updated in 2017) with a self-explanatory title, written by two of the most knowledgeable people about Google, Eric Schmidt and Jonathan Rosenberg. The former was the CEO of Google from 2001 to 2011 until he stepped down to be come “Executive Chairman” of Google (and then Alphabet later). So … basically he’s shuffling around titles without loss of power, I think.⁵ Jonathan Rosenberg⁶ was a longtime Product Manager for Google, and now he is advisor to Alphabet CEO Larry Page. These two men thus know a lot about Google and are well-qualified to talk about it. The book is an entertaining mix of the lessons they’ve learned about working at Google, how to scale it up, etc. I was particularly impressed about stories such as how Jeff Dean et al. found a note from the CEO who complained that “these ads suck”. So in one weekend, despite them not being on the ads team, they were able to fully diagnose the problem. Wow, that’s Google for you. The main takeaway from this book is that I need to be a better smart creative. The only way I know how to do this is by always learning, whether by coding or (as I try to do) read a lot of books. That being said, the book does suffer from trying to describe many concepts that I would argue are obvious and well-known. Many themes, such as “think 10x better, not incremental” are common in books that combine technology and business, such as Peter Thiel’s Zero to One book, which I read last year. Another is that “you can’t apply the lessons you learn in business school” which is again something commonly assumed in the tech industry. Another is “hiring is the most important thing you can do” but Joel Spolsky has already said something similar earlier on his blog. I don’t mean to completely negate the benefits of this book; it seems to maintain just enough of the “uniqueness” balance to make it a worthwhile read. Homer alert: I wish the authors would write a follow-up book where they discuss Artificial Intelligence. After all, current Google CEO Sundar Pichai has made it a point to emphasize AI for Google. To be fair, they mention it as one of the “things that might happen in the next five years”, so right now we’re smack dab in the middle of that time period. I’ll keep watch in case they publish a sequel later. On a final note, reading this book made me want to work at Google!

• ** Weapons of Math Destruction: How Big Data Increases Inequality and Threatens Democracy ** is a 2016 book by mathematician-turned-data scientist and author (and MathBabe founder) Cathy O’Neil who argues that the use of large datasets in industry and government contexts has, well, increased inequality in our society. She describes stories about how the use of big data to predict whether someone will commit a crime or default on a loan has a harmful feedback loop on the poor and minorities. (Blacks are the minority group emphasized the most in the book.) Why is there a feedback loop? Minorities are more likely to be around people who are committing crimes, and the “birds of a feather” mentality among big data algorithms is that they tend to relate people to those who bear similar qualities. Whereas in the past, for instance, a banker might not have relied on big data but on his instincts to grant or deny loans, which would hurt women and minorities, nowadays we mostly have data algorithms to determine that, but even so, algorithms have their own biases and values (indeed, this is an academic research topic, see the BAIR Blog post on this which also uses Google’s “labeling blacks as gorillas” example of algorithms trained on wrong data). O’Neil calls for increased transparency in these algorithms, which she calls Weapons of Math Destruction (WMDs), and for the people working on these algorithms to better understand the values that are inherent in the models. I enjoyed most of the short, fast-paced book and highly recommend it. It’s also worth noting that O’Neil regularly writes columns about this subject area, which interested readers should check out.

• ** Thank You for Being Late: An Optimist’s Guide to Thriving in the Age of Accelerations ** is Thomas L. Friedman’s most recent book, published in late 2016 (though the manuscript was done before the outcome of the presidential election). For a long time, I’ve been following Friedman’s Sunday weekly columns at The New York Times, which has served as a preview for what’s to come in the book: Moore’s Law, the refugee/migration crisis, unstable governments, droughts and climate change, and the polarization at the highest level of American politics. Friedman goes through these and discusses topics much like he did in The World is Flat, though I think he tempers his idiosyncratic writing style. He mentions at one point a handful of policy changes he’d like to do, and claims he’s neither left nor right politically and that those labels are now outdated. For instance, he’s very free trade (right) but also for single-payer health care (left). I was duly impressed from the book because it taught me much about how the world works today. It also made me appreciate that I’m in a position where I can take advantage of what the world has to offer. Thank You for Being Late also mentioned several technical topics that I’m passionate about. It was really nice to see a mainstream, “non-technophobe” talk about Moore’s Law, GitHub⁷, and even TensorFlow/Deep Learning (!!); he explained these topics as well as he could given the non-technical nature of the targeted audience. I also appreciated the surgeon general’s comment in the end that America’s biggest killer “was not heart disease, but isolation” which is ironic given how we are more connected than ever before. Ultimately, I want to be part of that acceleration and, of course, to ensure that the vast majority of Americans aren’t left behind (including myself!). The book, however, made me concerned about the future. I finished this just a few days before Trump was inaugurated so … hopefully things will be OK.

• What to Do When Machines Do Everything: How to Get Ahead in a World of AI, Algorithms, Bots, and Big Data is a recent 2017 book by three leaders from Cognizant, a firm which I didn’t know about beforehand. This book takes the now-standard view (at least among many technology thinkers) that automation will be overall better for us, destroying some jobs but also creating new ones and clearing out old drudgery. One thing the authors note which I haven’t heard before is that they subscribe to the “S-Curve”: we’re in a “stall” zone, but for the next two decades, we will experience dramatic economic growth with more equalizing effects as it relates to income distribution. I find this hard to believe, unfortunately. Another perspective the authors bring is that once old entrenched companies make more of a digital transition, that’s when we’ll really see GDP take off. Regarding the book style, it’s short and written in a mini-textbook style. The abbreviations in it were a bit corny but I enjoyed the examples, at least the ones they had. I surprisingly didn’t seem to enjoy it as much as some other similar books, probably because some of their advice is really high level and generic, over-simplifying things. All in all, I think the book is mostly correct on a technical level but may not be my style.

Group 3: Business and Economics

I badly need to better understand the world of business, particularly due to the increasing business-related importance of Artificial Intelligence nowadays.

• How the West Grew Rich: The Economic Transformation of the Industrial World. This is an old 1986 book by the late economist and historian Nathan Rosenberg and co-author L.E. Birdzell Jr, an attorney and legal scholar, and I have several quick thoughts. The first was that this book was a real slog for me to read. It’s not even close to being the longest book I’ve read⁸ but I had to struggle through it; I think the writing style of 1986 is different from the one I’m used to today, but I’m also partly to blame since I spaced out my reading over many evenings when I was tired. In any case, this book is about capitalism in some sense, though the authors complain that the term is misleading. Their main argument is that the freedom of business and enterprise from religious and political control was the key factor in explaining the rise of the West, and not other factors generally attributed, such as science or mass production. Judging from the book, the prevailing wisdom at that time may have been mass production, but apparently not to them. It’s a bit interesting to think about what conclusions they make which are still relevant today, like how it’s so hard for Third World countries to catch up. I was also amused at seeing the Soviet Union mentioned so much, and I had to remind myself: 1986, 1986, 1986. (In a shout-out to the AI people reading this, that was the year when Rumelhardt, Willimans, and Hinton published their famous backpropgation paper with “readable math”.) Ultimately, while this book has some good spots in it, I lost focus too much to really benefit from it, and I think The Rise and Fall of American Growth is a vastly superior alternative, unless you want to get a better understanding of European stuff (not just American) and also some discussion about the Middle Ages.

• Shop Class As Soulcraft: An Inquiry Into the Value of Work, is a 2009 book written by Matthew Crawford, who has one of the most unusual profiles among authors I read. Crawford is a mechanic and works at a bike shop, but he also holds an undergraduate degree in physics and a PhD in political philosophy from the University of Chicago. After his PhD, he worked at a “think tank” (where he had to basically repeat what the oil companies wanted to say about global warming) and at a firm where his job was to basically rewrite abstracts of research papers (what?!?). His true heart lies in building things, where he gets value. Crawford is concerned that today’s white-collar emphasis of the world focuses too much on removing value from humans (whereas mechanics can just point and say “here’s my result!”), and the white-collar blue-collar divide is making the mechanics earn less respect across society. I am indeed concerned that this is true, especially with today’s political divide among the college-educated and non-college educated, and I wish that more people with solid academics, those who have “never failed” had a little more humility. (I certainly feel like I’ve failed a lot and I’m pretty academically credentialed compared to a lot of others.) In a sense, I get the feeling that this book is like Jaron Lanier’s “You Are Not a Gadget” — those two men might see a lot of common ground over their critiques of modern life, though for different reasons. One takeaway from the book is that I’m happy to be where I am since I can try and perform deep work to produce results (code, papers, etc.) that people can look at, as I am doing more frequently on my GitHub account. Unsurprisingly, this was the key point Cal Newport made from this book. Lastly, I can’t resist mentioning one of the most interesting parts of this book. In a footnote in the seventh chapter, he talks about AI in the context of lamenting how humans were often being reduced to simple straightforward rules. His footnote talks about computer science and says the one hope for AI in the future is with neural networks since they’re not reduced to simple rules. Wow … that was in 2009 (before Alex-Net, etc.). Even your bike shop repairman knows about Deep Learning!

• ** The Lean Startup: How Today’s Entrepreneurs Use Continuous Innovation to Create Radically Successful Businesses ** is a 2011 book by software entrepreneur Eric Ries, known for co-founding IMVU and then later for consulting various start-ups through his Lean Startup methodology. In this book, Reis provides a guide for start-ups, which he defines as: “[…] a human institution designed to create a new product or service under conditions of extreme uncertainty”. Note the lack of any comment about company size, and also note the inclusion of extreme uncertainty. This means start-ups can include non-profits, large companies, and even governmental organizations, so long as there is initial uncertainty in their roadmap. The Lean Startup argues that, in order for startups to thrive, they must follow a Build-Measure-Learn feedback loop. Furthermore, that loop must be their competitive advantage compared to slower, bulkier competition. By building Minimum Viable Products, Reis argues that appropriate metrics (not “vanity metrics” as he calls them) and customer feedback can be measured rapidly. Understanding these early results then guides the startup towards the next step, which may or may not involve the painful act of pivoting to change strategies. The book’s advice appears sound and reasonable. While I certainly don’t have much experience in this area to fully critique the book, Reis has famous tech titans such as Sheryl Sandberg and Andrew Ng to vouch for the book, so I think I can trust the advice. (I found out about this book from Andrew Ng’s reading recommendations.) While reading the book, I imagined what I would do if I tried to create (or more realistically, join) a start-up. My PhD program isn’t going to last forever … but I suppose while I’m here, I should emphasize the Minimum Viable Product aspect with respect to research.

• ** The Hard Thing About Hard Things: Building a Business When There are No Easy Answers ** is a 2014 book by billionaire venture capitalist Ben Horowitz where he recounts his experience running Loudcloud and Opsware as CEO. The book starts out by first describing the CEO experience. Then, Horowitz remarks about the lessons he’s learned and outlines recommendations and guides on what he thinks CEOs should be like. The book concludes with him explaining how he founded the venture capital firm Andreessen Horowitz, which he’s still running today⁹ to help technical founders become groomed CEOs. The book is fast-paced and feels like a high-octance novel, because Horowitz’s tenure at Loudcloud and Opsware was anything but smooth. Horowitz argues that there are peacetime CEOs and wartime CEOs, of which he was definitely the latter as he estimates he only had “three days of peace” when running the company. Loudcloud and Opsware initially raised a lot of money, but then after the dot-com crash, they struggled a lot and I’m amazed that Horowitz turned it around and eventually sold the company for $1.6 billion to Hewlett-Packard. Reading his story, and Elon Musk’s story (which I’ll get to later), makes me wonder how these two CEOs managed to pull their companies out from the financial brink. I am kind of surprised that something “comes out of nothing,” and one of my disappointments is that it arguably spends a lot of time on Horowitz’s lessons for the CEO whereas I would have preferred more details on his CEO experience (at least, more than what’s in the book) because, again, I don’t understand how companies can go to a billion dollars’ worth of value out of nothing. I really need to step in the shoes of a CEO one of these days. But perhaps I would have better understood this if I understood more about business, and I certainly learned a lot about the business word from reading this book. For instance, I’m embarrassed to say that I only had a vague notion of what it meant for “a company to go public” but reading this book (and checking Wikipedia, Investopedia, and other online resources in parallel) made me better understand the process.

• ** The Rise and Fall of American Growth: The U.S. Standard of Living Since the Civil War ** is a long book by economist Robert Gordon, published in January 2016. For an academic-style book that’s 762 pages long, it is quite well-known, particularly due to the current debates on economic growth in politics. On Google, you can find pages and pages of reviews for Gordon’s book. Most of them mirror Bill Gates’ review in that they praise Gordon for providing a surprisingly complete historical picture of what American life was like in 1870, and how it was completely transformed in the “great century” to 1970. Gone were the days of darkness, backbreaking labor, endless drudgery in chores, and a stale diet, among other things, and in place of those came the electric light bulb, work conditions in heated and air-conditioned offices, the internal combustion engine (leading to automobiles and the airplane), and shopping centers to buy a variety of food and clothes. Gordon’s thesis is that since 1970, America has been in a long reign of slow growth despite the recent progress in AI, IT, and other tech-related fields. There are two reasons: these advances do not match up with those from previous generations (to echo Peter Thiel, “we wanted flying cars but ended up with 140 characters [Twitter]”), and there are headwinds preventing rapid growth such as income inequality, college debt, and demographic trends. He ends with a brief postscript on policy actions that might be useful to counter these trends; I wish more politicians would take note of them as some of his suggestions have broad appeal nowadays. This book is amazing, and despite my close connection with the technology sector, I agree with his thesis. Bill Gates counters by suggesting we’re on the cusp of medical advances, but I’m heavily skeptical about researchers finding cures for cancer and Alzheimer’s disease. It might be challenging for the average reader to go through a book this long, especially one packed with figures and footnotes. My advice? Read it. It’s worth it. I have probably learned more from this book than I have from any other.

Group 4: Biographies and Memoirs

I am reading biographies of famous people because I want to be famous someday. My aim is to be famous for a good reason, e.g., developing technology that benefits large swaths of humanity. (It is obviously easier to become famous for a bad reason than a good reason.)

• ** Alan Turing: The Enigma ** is the definitive biography of Alan Turing, quite possibly the best computer scientist of all time. The book was written in 1983 by Andrew Hodges, a British mathematics tutor at the University of Oxford (now retired). I discussed this in a separate blog post so I will not repeat the details here.

• ** My Beloved World ** is Supreme Court Justice Sonia Sotomayor’s memoir, published in 2013. It’s written from the first person perspective and outlines her life from starting in South Bronx and moving up to her appointment as a judge to US District Court, Southern District of New York. It — unfortunately — doesn’t talk much about her experiences after that, getting appointed to the United States Court of Appeals for the Second Circuit in 1998, and of course, her time on the nation’s highest court starting in August 2009. She had a father who struggled with alcoholism and died when she was nine years old, and didn’t appear to be a good student until she was in fifth grade, when she started to obsess over getting “gold stars.” (I can attest to a similar experience over obsessing to get “gold star-like” objects when I was younger.) She then, as we all know, did well in high school and entered Princeton as one of the first incoming batch of women students and Hispanic students, graduating with stellar academic credentials in 1976 and then going on to Yale Law School where she graduated in 1979. The book describes her experiences in vivid terms, and I liked following through her footsteps. I feel and share her pain at not knowing “secrets” that the rich and privileged students had when I was an undergrad (I was clueless about how finance and investment banking jobs worked, and I’m still clueless today.) Overall, I enjoyed the book. It’s brilliantly written, with an engrossing, powerful story. I will be reminded of her key attribute of persistence and determination and focus which she says were key. I’m trying to pursue the same skills myself. While I understand the low likelihood of landing such tiny jobs (e.g., the tech equivalent of a Supreme Court Justice) I do try and think big and that’s what motivates me a lot. I read this book on a day trip where I was sitting in a car passenger seat, and I sometimes dozed off and imagined myself naming various hypothetical Supreme Court Justices.

• An Appetite for Wonder: The Making of a Scientist is Richard Dawkins’ first of two (!!) autobiographies, published in 2013 and which accounts for the first half of his life. Dawkins is one of the most famous and accomplished scientists today, not only in terms of raw science but also with respect to public outreach and fame (whether famous, in my opinion, or infamous, if otherwise), so perhaps two books is justified. Dawkins discusses his childhood, which he first spent in Africa before moving to England to attend boarding schools; he remarked that the students seemed to be relatively stronger in Africa. I sometimes wish I had attended boarding schools instead of my standard public schools, since perhaps I would have developed independence faster, so it was interesting to read his perspective. After this, Dawkins talks about his undergraduate years at Oxford¹⁰ (where his relatives had gone) and this is where I really want to know what he did, because I’m hoping to use my own “appetite for wonder” in science, since I think Artificial Intelligence is the new electricity. But anyway, Dawkins became a professor at Berkeley (!!) but he quickly left to return to England for another position. This book ends with his publication of The Selfish Gene, a book that I want to read one of these days. I’m impressed: it’s a challenge to write an autobiography, but fortunately, Dawkins’ parents saved a lot of letters and information, so that’s good. The book, however, is likely aimed at a niche audience of readers. It was also interesting to Dawkins used to be religious, before becoming an atheist by his late teens (like me, though I was never religious at all). I also liked his stories about computer programming and research, which were a lot simpler back then but presumably harder due to lack of documentation and the Internet.

• Brief Candle in the Dark: My Life in Science is Richard Dawkins’ second autobiography, written in 2015 and covering the second half of his life, at least, up to that point (he could theoretically still have 30 more years if he lives long enough). He writes more about his life as a professor at the University of Oxford, including his time as the inaugural Simonyi “Professor of the Public Understanding of Science,” which I have to admit was an odd title when I first read it in the back flap of my copy of The God Delusion. He certainly has helped me understand things in this world, and it’s true that I consider Richard Dawkins to be one my heroes. On the other hand, I’m not sure most lay readers would be willing to slog through both of his autobiographies, so keep this in mind in case you’re on the fence about reading this book. It is a non-chronological history of his academic life about debates (uh oh), being on television, writing books, giving talks, and so forth. Dawkins describes various stories about him with other famous people. I also learned a little more about basic evolution. His previous autobiography highlighted how genes — and not the individual — are the unit of evolution, but in his book The Extended Phenotype, he talks about an extension of natural selection onto the physical world (interesting, though one must not misinterpret this). He also emphasizes, and this is something I agree with, that natural selection can still explain complicated structures today that creationists use as evidence against evolution, such as the eye. Natural selection is the only theory we have of what can work gradually and cumulatively. This is key for developing complicated structures; in the absence of evidence, God should not be the default option. I also liked other tidbits of the book, such as how Dawkins did a lot of “evolutionary programming” — I bet he would be interested in reading the research paper Evolution Strategies as a Scalable Alternative to Reinforcement Learning.

• ** Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic Future ** is a 2015 biography of Elon Musk, written by technology journalist Ashlee Vance. He documents Musk’s chaotic life, both nowadays as the CEO of SpaceX and Tesla and before, when he was struggling to get his companies off the ground and earlier still, when he started his entrepreneurial spirit by starting Zip2. Musk grew up in South Africa and moved to Canada so that he could get to the United States as quickly as possible. Musk had some initial businesses successes, but was forced out of X.com (which particularly hurt as Musk is the personality who wants full control over his companies), then earned some more success with Tesla and SpaceX before teetering on the brink of collapse at the end of 2008 (you know, like the financial “oopsie” we had). Then later, those companies recovered, Musk married a young actress, divorced, then re-married (then divorced again …). The book concludes with some thoughts on Musk’s wild personality and ambitions, and basically says that there is no one like Musk, who still is holding out hope for humans to go to Mars by 2025. This book is an absolute thrill to read. Vance brilliantly writes it so that the reader often feels like he or she is swept up into “Elon Musk”-mode: hard-working, super-charging, and borderline out of control. After reading it, I kept thinking that my work ethic is too soft and weak, and that I better get back to working sixteen hours a day (or less, if I’ve focused really hard in fewer hours). I have two main criticisms of this book. The first is that I was hoping to see more information from his two wives, and for this I’ll probably have to relegate myself to reading Justine Musk’s blog. The second and most important critique is that when Vance wrote an updated epilogue in January 2017, which was five months before I bought the book at Chicago O’Hare International Airport, he never mentioned Musk’s investment in OpenAI, a nonprofit AI research company which aims to produce, or pave the path to, artificial general intelligence. In their introductory blog post from December 2015, they claim to have 1 billion dollars in investment. I’m not sure how much Musk contributed to that, but it must have been a lot!

• Keeper of the Olympic Flame: Lake Placid’s Jack Shea vs. Avery Brundage and the Nazi Olympics, a recent 2016 book by Michael Burgess, is one that hits home to me because Jack Shea was my great-uncle. Jack Shea was born and raised in Lake Placid, New York, and as a 21-year-old competitor in the 1932 Winter Olympics, he won two gold medals in speed-skating, becoming a hometown hero and putting Lake Placid “on the map.” A few years later, when it became apparent that the next Winter Olympics were going to be in Nazi Germany, Shea urged Avery Brundage (then in charge of American involvement in the Olympics) to boycott out of concerns over Adolf Hitler’s treatment of Jews and other minorities. Shea did not participate in those controversial Olympics, but the Americans did send a team, with relatively disappointing speed-skating results. The book then discusses more about the intersection between politics and sports, and also talks about the odd déjà vu when Lake Placid again hosted the Winter Olympics in 1980, again with politics causing tension (this time, from the Soviet Union). For obvious reasons, I enjoyed reading this book despite its flaws: it’s short and has obvious typos. I like knowing more about my ancestors and what they did, and the photos were really striking. My favorites include 19-year-old Shea shaking hands with then-governor Franklin Roosevelt, another one with Shea and his extended family (including my grandfather), and a third which shows a pre-teen Shea and his brother, Eugene, already in skates. Eugene, incidentally, lived to be 105 years old (!!) before passing away in October this year (obituary here) and was able to contribute photos and assistance to the author. I got to meet Jack Shea once, and he might very well have lived to be 100 years of age had he not been killed by a drunk driver at the age of 91. This was 17 days before his grandson would end up winning a gold medal in the 2002 Salt Lake City Winter Olympics. In my parent’s home, there is a photo of me with my cousin holding his gold medal (it was heavy!). I also have a separate blog post about this book soon after I read it.

Group 5: Conservative Politics and Thoughts

Well, this will be interesting. I’m not a registered Republican, though I possess a surprisingly large amount conservative beliefs, some of which I’m not brave enough to blog about (for obvious reasons). In addition, I believe it is important to understand people’s beliefs across the political spectrum, though for this purpose I exclude the extreme far left (e.g., hardcore Communists) and right (e.g., the fascists and the Ku Klux Klan).

• ** Please Stop Helping Us: How Liberals Make it Harder for Blacks to Succeed ** a 2014 book written by Wall Street Journal columnist Jason Riley. It’s no secret that (a) most blacks tend to be liberal, I would guess due to the liberals getting the civil rights movement correct in the 1960s, and (b) blacks tend to have more credibility when criticizing blacks compared to whites. Riley, as a black conservative, can get away with roundly criticizing blacks in a way that I wouldn’t do since I do not want to be perceived as a racist. In Please Stop Helping Us, Riley “eviscerates nonsense” as described by his hero, Thomas Sowell, criticizing concepts such as the minimum wage, unions, young black culture, and affirmative action policies, among other things, for the decline in black prosperity. His chief claim is that liberals, while having good intentions, have not managed to achieve their desired results with respect to the black population. He also laments that young blacks tend to watch too much TV, engage in hip-hop culture, and the like. One of his stories that stuck with me was when a young (black) relative asked him: “why are you so white”, when all Riley did was speak proper English and tuck in his shirt. Indeed, variants of this story are common complaints that I’ve seen and heard about from black students and professionals across the political spectrum. I don’t agree with Riley on everything. For instance, Riley tends to ignore or explain away issues regarding racism as it relates to the lack of opportunities for job promotions or advancement, or when blacks are penalized more relative to others for a given crime. On the other hand, we agree on affirmative action, which he roundly criticizes, pointing out that no one wants to be the token “diversity hire”. To his credit, he additionally mentions that Asians are hurt the most from affirmative action, as I pointed out in an earlier blog post, making it a dubious policy when it come to advancing racial equality. In the end, this book is a thought-provoking piece about race. My impression is that Riley genuinely wants to see more blacks succeed in America (as I do), but he is disappointed that the major civil rights battles were all won decades ago, and nowadays current policies do not have the same positive impact factor.

• ** The Conservative Heart: How to Build a Fairer, Happier, and More Prosperous America **, is a 2015 book by Arthur Brooks, the president of the American Enterprise Institute, officially a nonpartisan think tank but widely regarded (both inside and outside the organization) as a place for conservative public policy development and analysis. Brooks argues that today’s conservatives, while they have most of the technical arguments right (e.g., on the benefits of free enterprise), lack the “moral high ground” that liberals have. Brooks cites statistics showing that conservatives are seen as less compassionate and less caring than liberals. He argues that conservatives can’t be about being anti-everything: government, minimum wage increases, food stamps, etc. Instead, they have to show that they care about people. They need to emphasize an equal starting line for which people can flourish, which contrasts with the common liberal perspective of making the end product equal (by income redistribution or proportional racial representation). One key point Brooks emphasizes is the need for work fulfillment and purpose instead of lying around while collecting checks from the American welfare state. I liked this book and found it engaging and accessible. It is, Brooks says, a book for a wide range of people, including “open-minded liberals” who wish to understand the conservative perspective. I have two major issues with his book, though. The first is that while he correctly points out the uneven recovery and the lack of progress on fixing poverty, he fails to mention the technological forces that have created these uneven conditions (see my technology, economics, and business related books above), much of which is outside the control of any presidential administration or Congress. The second is that I think he’s been proved wrong on a lot of things. President Donald Trump is virtually none of the stuff that a conservative “heart” would suggest and, well, he was elected President (after this book was published, to boot). I wish President Trump would start following Brooks’ suggestions.

• Conscience of a Conservative: A Rejection of Destructive Politics and a Return to Principle is a brief 2017 book/manifesto by U.S. Senator Jeff Flake of Arizona. Flake is well known for being one of those “Never Trump” style of Republicans since he remains true to certain Republican principles that have arguably fallen out of favor with the recent populist surge of Trump-ian Republicanism in 2016, such as free trade and limited government spending. And yes, I don’t think Republicans can claim to be the party of fiscal prudence nowadays, since Trump is decidedly not a limited spending conservative. In this book, Senator Flake argues that Republicans have to get back to true, Conservative principles and can’t allow populism and immaturity to define their party. He laments at the lack of bipartisanship in Congress, and while he makes it clear that both parties are to blame, in this book he mostly aims at Republicans. This explains why so many Republicans, including Barry Goldwater’s relatives, dislike this book. (Barry Goldwater wrote a book of the same title, “Conscience of a Conservative”, from which Jeff Flake borrowed the title.) I sort of liked this book but didn’t really like it. It still fails to address the notion of how the parties have fallen apart, and he (like everyone else) preaches bipartisanship without proposing clear solutions. Honestly, I think the main reason I read it was not that I think Flake has all the solutions, but that I sometimes think of myself in Congress in my fantasies. Thus, I jumped at the chance to read a book directly from a Congressman, and particularly a book like this where Flake bravely didn’t have his staff revise it to make it more “politically palatable.” It’s a bit raw and lacks the polish of super-skilled writers, but we shouldn’t hold Senators to such a high writing standard so it’s fine with me. It’s unfortunate that Flake isn’t going to seek re-election next year.

Group 6: Self-Help and Personal Development

I’m reading these “personal development” books because, well, I want to be a far more effective person than I am right now. “Effectiveness” can mean a lot of things. I define it as being vastly more productive in (a) Artificial Intelligence research and (b) my social life.

• ** How to Win Friends and Influence People: The Only Book You Need to Lead You to Success ** is Dale Carnegie’s famous book based on his human interaction courses. It was originally published in 1936, during the depths of the Great Depression, making this book by far the oldest one I’ve read this year. I will not go into too much depth about it since I wrote a summary in an earlier blog post. The good news is that 2017 has been a much better year for me socially, and the book might have helped. I look forward to continuing the upward trend in 2018, and to read other Dale Carnegie books.

• ** The 7 Habits of Highly Effective People: Powerful Lessons in Personal Change **, written by Stephen R. Covey in 1989, is widely considered to be the “successor” to Dale Carnegie’s classic book (see above summary). In The 7 Habits, Covey argues that the habits are based on well-timed principles and thus do not noticeably vary across different religious groups, ethnic groups, and so forth. They are: “Be Proactive”, “Begin With the End in Mind”, “Put First Things First”, “Think Win-Win”, “Seek First to Understand, Then to be Understood”, “Synergize”, and “Sharpen the Saw”. You can find their details on the Wikipedia page so I won’t repeat the points here, but I will say that the one which really touches upon me is “Think Win-Win”. In general, I am always trying to make more friends, and I’d like these to be win-win. My strategy, which aligns with Covey’s (great minds think alike!), is to start a relationship by doing more work than the other person or letting the other person benefit more. Specifically, this means that I will be happy to (a) take the initiative in setting meeting times and any necessary reservations, (b) drive or travel farther distances, (c) let the other person choose the activity, and so forth. At some point, however, the relationship needs to be reciprocal. Indeed, I often tell people, subtly or not so subtly, that the true test of friendship is if friends are willing to do things for you just as much as you do to them. With respect to the six other principles, there isn’t much to disagree. There is striking similarity to Cal Newport’s Deep Work when Covey discusses high-impact, Quadrant II activities. Possibly my main disagreement with the book is that Covey argues how these principles come (to some extent) from religion and God. As an atheist, I do not buy this rationale, but I still agree with the principles themselves and I am trying to follow them as much as I can. This book has earned a place on my desk along with Dale Carnegie’s classic, and I will always remember it because I want to be a highly effective person.

• You are a Badass: How to Stop Doubting Your Greatness and Start Living an Awesome Life is a 2013 book by self-help guru Jen Sincero. It’s deliberately written in a very “teenage”-like way, where the author acts like she’s talking directly to the reader as the self-help coach. The target audience seems to be people who have “screwed up” and feel like their life is not as awesome as it could be. She goes through 27 relatively short chapters, each with different generic advice, though she does repeat this each chapter: love yourself. I definitely need reminders about that, since I don’t feel like I am achieving enough in life. However, I was somewhat skeptical of her advice and in general I am a self-help skeptic since I think it’s better for me to build my technical skills than to try and optimize advice from self-help books. Overall, I did not enjoy this book (largely due to the writing style), and I’m surprised it’s gotten so much critical acclaim and that it’s a best-seller. Yes, I will “love myself” but I can’t see myself remembering many other tidbits about this book that I didn’t already know before (e.g., think positive!!). Perhaps this book would be better suited with some concrete success stories of Sincero’s clients.

Group 7: Psychology and Human Relationships

These books are about psychology, broadly speaking, which I suppose can include “human relationships”. I thoroughly enjoyed reading all four of these books.

• ** Thinking, Fast and Slow ** is a famous 2011 book by Daniel Kahneman, winner of the 2002 Nobel Prize in Economics for his work on decision making. This is a book about psychology and how humans think, and much of it is based on Kahneman’s research with Amos Tversky many decades ago. To make the concepts clearer to the reader, Kahneman describes a story consisting of System 1 and System 2. These are the fast and slow parts of our thinking, respectively, so the former represents our immediate intuition and the latter reflects what happens after we expend nontrivial amounts of effort on some task. Thinking, Fast and Slow is filled with informative anecdotes, thrilling insights, and unexpected contradictions about the way humans think, and supplements those with exercises to the reader. (I normally find these annoying, but here they were reasonable.) Possibly the biggest insight I gained is that human thinking is flawed and is easily manipulated, so I better be extra cautious if I have to make important judgments in my life. (For minor life decisions, I don’t have a hope of remembering all the advice in this 400+ page book.) To be clear, I already knew that humans behaved irrationally, but Kahneman does an excellent job in putting my haphazard thoughts about human irrationality on more solid footing. Kahneman augments that with related topics such as overconfidence (a major issue with CEOs and start-ups) and how anchoring, priming, and baselines influence human preferences. After reading the book, all I can say is, I think (pun intended!) Thinking, Fast and Slow lives up to its billing as a true classic.

• ** To Sell Is Human: The Surprising Truth About Moving Others ** is a 2012 book by best-selling author Daniel Pink. He argues that we should stop focusing on outdated views of salespeople. That is, that they are slimy, conniving, attempting to rip of us off, etc. Today, one in nine work in “sales” but Pink’s chief message to the reader is that the other eight of nine are also in sales. We try to influence people all the time. So in some sense this is obvious. I mean, if I am aiming to get a girlfriend, then I’m trying to influence her based on my positive qualities. For academics, we sell our work (i.e., research) all the time. That’s what Pink means when he says “everyone is working in sales.” He argues that nowadays, the barriers have fallen (he almost says “The World is Flat” a la Thomas L. Friedman) and that salespeople are no longer people who walk door by door to ask people to buy things. That’s outdated. One possible negative aspect of the book is that I don’t think we need this much “proof” that we’re all salespeople. Yes, some people think only in terms of that job, but all you have to do is say: “hey everyone is a salesperson, if you try to become friends with someone, that counts…” and if you tell that to people, all of a sudden they’ll get it and I don’t think belaboring the point is necessary. On the positive side, the book contains several case studies and lists of things to do, so that I can think of these and reread the book in case I want to apply them in my life. Indeed, as I was reading this book, I was also thinking of ways I could convince someone to become friends with me.

• ** Lean In: Women, Work, and the Will to Lead ** is a well-known 2013 book by Facebook COO Sheryl Sandberg. It’s a semi-memoir which also acts as a manifesto for women (and men) to be more aware of the gender gap in “prestigious positions” and how to counteract it. By such “prestigious positions” I mean CEOs (particularly of top companies), politicians, and other leadership positions. Women occupy fewer of these positions than men in virtually every country in the world, and Sandberg wants this to change. She outlines numerous factors that hold women back, not all of which are obvious. Her first example deals with parking spots reserved for pregnant women, in which she admits she (despite being a woman!) didn’t think about until she became pregnant herself. Pregnancy is a major focus in this book, along with work-life balance, a typical inclusion in books about women and careers. Sandberg also recounts stories about women being quiet in meetings or not taking seats in the center of a meeting table even when prompted to do so, and lowering their hands when people say there are no more questions (despite how men keep their hands up and thus get to ask more questions). This forms the overall basis for her advice that women must “lean in” and be more involved in discussions. I liked reading this fast-paced book but I also almost felt disappointed, since I anticipated much of the material in advance. Perhaps it’s because I read about gender-related issues frequently. Another possible explanation is that it is hard for me to participate in group meetings, so I often spend more time observing people and noticing things rather than focusing on the subject at hand. On a final note, I’d like to mention that I do, in some sense, believe that “other men are the problem, not me” though I would never say this in public to someone, because (a) it’s politically charged, and (b) I could, of course, make a mistake in the future and thus I would be hypocritical and have to eat my own words. In my adult life, I do not believe I have ever done anything blatantly sexist, though I certainly worry a lot about committing “microaggressions” when I interact with women, and do my best to avoid them to make my female (as well as male) conversationalists feel respected and comfortable.

• ** Originals: How Non-Conformists Move the World ** is a recent 2016 book by famous Wharton professor Adam Grant, also known as the author of Give and Take. I’ve been aware of Grant for some time, in part because he’s been featured in Cal Newport’s writing as someone who engages in the virtues of Deep Work (see an excerpt here). Yeah, he’s really productive, finishing a PhD in less than three years¹¹ and then becoming the youngest tenured professor at his university. But what is this book about, anyway? In Originals, Grant argues that people who “buck the trend” are often ones who can make a difference for the better. As I anticipated ahead of time, Martin Luther King Jr is in the book, but not for all the reasons I thought. One of them — why procrastination might actually have been helpful (i.e., first mover disadvantage) for him when he was crafting his “I Have a Dream” speech, though one was more realistic: focusing on the victims of crimes (blacks facing discrimination) rather than criticizing the perpetrators. Another nice tidbit from Grant was making sure to emphasize the downsides of your work rather than the positives to venture capitalists, as that will help you look more sincere. Other stuff in this book include how to foster a correct sense of dissent in a company (e.g., Bridgewater Associates is unique in this regard because people freely criticize the billionaire founder Ray Dalio). I certainly felt like some of this was cherry-picking, which admittedly is unavoidable, but this book seems to pursue that more than others. Nonetheless, a lot of the advice seems reasonable and I hope to apply it in my life.

Group 8: Miscellaneous

These books, in my opinion, don’t neatly align in one of the earlier groups.

• ** Knocking on Heaven’s Door: How Physics and Scientific Thinking Illuminate the Universe and the Modern World ** is Harvard physics professor Lisa Randall’s second of three major books. Last year, I read her most recent book Dark Matter and the Dinosaurs, so this is “going back” in time back to 2011. Sorry, I know should have read them in order. But anyway, this book is a fascinating exploration of what I argue are two major topics. First, the Large Hadron Collider — the well-known experimental setup that revealed the Higgs Boson particle in 2012 and earned Peter Higgs an Nobel Prize. Randall describes how the experiment was set up in great detail, but with juuuuuust enough clarity for non-physicists like me to barely follow. I don’t have much knowledge about the LHC, and indeed I didn’t even know it was a fantastic engineering feat; it is an enormous system built deep underground in Europe, as the pictures in the book helped to illuminate. The second major part of the book is about scientific thinking itself: why do scientists revise theories, why is the notion of scale important, why is quantum mechanics important at smaller distances, but why can we “average out” its effects with Newtonian physics? I learned a little about how the Standard Model in physics works, and it was great to see how she describes the scientific approach to thinking. Randall also discusses cosmology in this book, but it’s much shorter relative to particle physics and feels slightly out of place, but fortunately any reader who wants an overview in cosmology should just read Dark Matter and the Dinosaurs. Overall, this is a book that somehow remains fascinating and mostly accessible despite all the physics facts and jargon. It’s tricky to write science books for the general public. Randall does a good job in that when I was reading the book and felt somewhat confused at the jargon, I felt like it was my fault for my incompetence, and not hers. I am now thinking about reading her first book, Warped Passages, or her e-book on the Higgs Discovery. I’ll definitely be on the lookout for any future books she publishes!

• ** The Signal and the Noise: Why So Many Predictions Fail – But Some Don’t ** is Nate Silver’s 2012 book where he urges us to consider various issues that might be adversely affecting the quality of predictions. They range from the obvious, such as political biases which affect our assessment of political pundits (known as “hedgehogs” in his book), and perhaps less obvious things such as a bug in the Deep Blue chess program which nonetheless grandmaster Gary Kasparov took to meaning that Deep Blue could “predict twenty moves into advance.” I really enjoyed this book. The examples are far ranging: how to detect terrorist attacks (a major difficulty but one with enormous political importance) to playing poker (Silver’s previous main source of income), to uncertainties involving global warming models (always important to consider), and to the stock market (this one is hardest for me to understand given my lack of background knowledge on the stock market, but I am learning and working to rectify this!). The one issue I have is that Silver seems to just assume: hey let’s apply Bayes’ rule to fix everything, so that we have a prior of \(X\), and we assume the probability of \(Y\) … and therein lies the problem. In real settings we rarely get those \(X\) and \(Y\) values to a high degree of accuracy. But I have no issue with the general idea of revising predictions and using Bayes’ rule. I encourage you to see a related critique in The New Yorker. The reality, by the way, is that most current professional statisticians likely employ a mix of Frequentist and Bayesian statistics. For a more technical overview, check out Professor Michael I. Jordan’s talk on Are You A Bayesian or a Frequentist?.

• ** The Soul of an Octopus: A Surprising Exploration into the Wonder of Consciousness ** is a splendid 2015 book by author Sy Montgomery, who has written numerous biology-related books about animals. I would call this entirely a popular science book; it’s more like a combination of the author discovering octopuses and describing her own experience visiting the New England aquarium, learning how to scuba dive, watching octopuses having sex in Seattle, and of course, connecting with octopuses. To be frank, I had no idea octopuses could do any of the things she mentions in the book (such as walking on dry land and squeezing through a tiny hole to get out of a tank). Clearly, aquariums have their hands full trying to deal with octopuses. Much of the book is about trying to connect with the three octopuses the New England aquarium has; the author regularly touches and feeds the octopuses, observing and attempting to understand them. I was impressed by the way Montgomery manages to make the book educational, riveting, and emotional all at once, which was surprising to me when I found out about the book’s title. It’s surely a nice story, and that’s what I care about.

• Nothing Ever Dies: Vietnam and the Memory of War is a book by USC English Professor Viet Thanh Nguyen, published in 2016 and a finalist for the National Book Award in Non-Fiction that same year. It’s not a recap or history of the Vietnam War (since that subject has been beaten to death) but instead it focuses specifically on how people from different sides (obviously, American and Vietnamese, but also the rest of the world) view the war, because that will shape questions such as who is at fault and should make reparations and also how we can avoid similar wars in the future. It’s an academic-style book, so the writing is a bit dry and it’s important not to read this when tired. I think it provides a useful perspective on the Vietnam War and memories in general. Nguyen travels to many areas in Vietnam and Asia and explores how they view America — for instance, he argues that South Korea attempts to both ally with the US and look down on Vietnam with contempt. I found the most thought-provoking discussion to be about identity politics and how minorities often have to be the ones describing their own experiences. I’ve observed this in the books I read, in which if they’re written by a minority author (and here I’ll include Asians despite how critics of the tech industry bizarrely decide otherwise) are often about said minority. Other interesting (though obvious) insights include how the entire war machine and capitalism of the US means it can spread its memories of the war more effectively than Vietnam can. Thus, the favorable American perspective of the US as attempting to “save” minorities is more widespread, which puts America in a better light than (in my opinion, channeling my inner Noam Chomsky) it deserves.

• The Once and Future Liberal: After Identity Politics is a short book (describing it as an essay is probably more accurate) written by humanities professor Mark Lilla of Columbia University. This book grew out of his fantastic (perhaps my all-time favorite) Op-Ed in the NYTimes about the need to end identity politics, or specifically identity liberalism. I agree wholeheartedly; we need to stop treating different groups of people as monolithic. Now, it is certainly the case that racism or mistreating of any group must be called out, and white identity politics is often played on the right, versus the variety of identities on the left. Anyway, this short book is split into three parts: anti-politics, pseudo-politics, and politics, but this doesn’t seem to have registered much to me, and the book is arranged in a different style as I might have hoped. I was mostly intrigued by how he said Roosevelt-esque liberalism dominated from roughly 1930 to 1970. Then the Reagan-esque conservatism (i.e., the era of the individual) has dominated from 1980 to 2016 or so, and now we’re supposed to be starting a new era as Trump has demolished the old conservatism. But Lilla is frustrated that modern liberalism is so obsessed about identity, and quite frankly, so am I. He is correct, and many liberals would agree, that change must be aimed locally now, as Republicans have dominated state and local governments, particularly throughout the Obama years. I do wish, however, that he had focused more directly on (a) how groups are not monolithic, (b) why identity politics is bad politics. I know there was some focus, but there didn’t seem to be enough for me. But I suppose, this being a short essay, he wanted to prioritize the Roosevelt-Reagan parallels, which in all fairness is indeed interesting to ponder.

• ** Climate of Hope: How Cities, Businesses, and Citizens can Save the Planet **, a 2017 book jointly written by Michael Bloomberg and Carl Pope. Surprisingly, considering that I was born and raised in New York state all my life (albeit, upstate and not in the city) the first time I really learned about Bloomberg was when he gave the commencement speech at my college graduation. You can view the video here, and in fact, to the right you can barely see the hands of a sign language interpreter who I really should re-connect with sometime soon. Climate of Hope consists of a series of chapters, which are split into half from Bloomberg’s perspective, half from Pope’s perspective. The dynamics between the two men are interesting. Pope is a “typical” Sierra Nevada member, while Bloomberg is known for being a ridiculously-rich billionaire and a three-term (!!) mayor of New York City.¹² The book is about cities, businesses, and citizens, and the omission of national governments is no accident: both men have been critical of Washington’s failure to get things done. Bloomberg and Pope aim their ire at the “climate change deniers” in Washington, though they do levy slight criticism on Democrats for failing to support nuclear power. They offer a brief scientific background on climate change, and then argue that new market forces and the rise of cities (thus greener due to more public transportation and more cramped living quarters) means we should be able to emphasize more renewable energy. One key thing I especially agree with is that to market policies that promote renewable energy — particularly to skeptical conservatives — people cannot talk about how “worldwide temperatures in 2100 will be two degrees higher.” Rather, we need to talk about things we can do now, such as saving money, protecting our cities, creating construction jobs, protecting our health from smog, all these thing we can do right now and which will have the effect of fighting long-term climate change anyway. I enjoyed this easy-to-read and optimistic book, though it’s also fair to say that I tend to view Bloomberg quite favorably and honor his commitment to getting things done rather than having dysfunction in Washington. Or maybe I just want to obtain a fraction of his professional success in my life.

That’s all for 2017!

---

It took me six and a half years to do this, but I finally managed to install an email subscription form for readers of this blog. The link is here. No more nasty RSS feeds that no one knows how to use!

The email subscription form for this blog uses MailChimp. Each time I publish a post, I will send an email to everyone on the list using MailChimp’s “Campaign” feature.

Incidentally, this is the same kind of email form we use over at the Berkeley AI Research (BAIR) Blog. If you haven’t already, please subscribe to the BAIR Blog! As a member of the editorial board, I know the posts that are coming up next. I obviously cannot reveal the exact content, though I can say that we have lots of interesting stuff lined up for 2018 and beyond.

For assistance on getting this set up, I thank Jane Liang, a UC Berkeley EECS student who set up MailChimp for the BAIR Blog. I also thank Dominic Spadacene, who wrote dead-simple HTML installation instructions on his Ctrl-F’d blog.

For a long time, I wanted to write a nice, long, friendly blog post on Hamiltonian Monte Carlo that I could come back to for more intuition and understanding as needed.

Fortunately, there’s no need for me to invest a ginormous amount of time I don’t have for that, because physicists/statistician Michael Betancourt has written a fantastic introduction to Hamiltonian Monte Carlo, called A Conceptual Introduction to Hamiltonian Monte Carlo. You can find the preprint here on arXiv. Don’t be deterred by the length; it’s a fast read compared to other academic papers, and certainly a much more intuitive read than Radford Neal’s 2011 review chapter, which I already thought couldn’t be surpassed in terms of a quality introduction to HMC. Indeed, even prominent statisticians such as COPSS Presidents’ Award winner Andrew Gelman have praised the writeup, and someone like him obviously doesn’t need it.

I have extensively read Radford Neal’s writeup, to the point where I was able to reproduce almost all his figures in my MCMC and Dynamics code repository on GitHub. There was, however, one question I had about HMC that I didn’t feel was elaborated upon enough:

Why is it necessary to flip the sign of the momentum to induce a symmetric proposal?

Fortunately, Betancourt’s writeup comes to the rescue! Thus, in this post, I’d like to go through the details on why it is necessary to flip the sign of the momentum term in HMC.

Let \(\mathbb{Q}(q' \mid q)\) be the density function defining the current proposal method, whatever that may be. With a Gaussian proposal, we have symmetry in that \(\mathbb{Q}(q'\mid q) = \mathbb{Q}(q\mid q')\). The same is true with Hamiltonian Monte Carlo … if we handle the momentum term correctly.

Borrowing Betancourt’s notation (from Section 5.2), we’ll assume that, starting from state \((q_0,p_0)\), we integrate the dynamics for \(L\) steps to land at \((q_L,p_L)\), upon which we use that as our proposal:

\[\mathbb{Q}(q',p' \mid q_0,p_0) = \delta(q'-q_L) \delta(p'-p_L)\]

where \(\delta: \mathbb{R} \to \{0,1\}\) is the Dirac delta function, and the difference \(q'-q_L\) is assumed to be real-valued; if \(q\) and \(p\) are vectors, these would need to be done component-wise and then summed up, but the same basic idea holds. Furthermore, \(q'\) and \(p'\) are “placeholder” random variables, kind of like how we often use \(X\) when writing \(\mathbb{P}[X=x]\) in introductory probability courses; \(X\) is the placeholder and \(x\) is the actual quantity.

Reading the definition straight from the Dirac delta functions, we see that our proposal density is one exactly at state \((q',p')=(q_L,p_L)\), and zero everywhere else. This makes sense because Hamiltonian dynamics are deterministic after re-sampling the momentum variables (but it’s understood that \(p_0\) represents those states after the re-sampling, not before).

The problem with this is that the proposal becomes “ill-posed”. Betancourt remarks that:

\[\frac{\mathbb{Q}(q_L,p_L \mid q_0,p_0)}{\mathbb{Q}(q_0,p_0 \mid q_L,p_L)} = \frac{1}{0}\]

however, I believe that’s a typo and that the numerator and denominator should be flipped, so that the numerator contains the density of the starting state given the proposal.

Regardless, to me it doesn’t make sense to have proposal probabilities or densities with these Dirac delta functions that result in zero everywhere (that means we’d always reject samples). The following figure (from Betancourt) visually depicts the problem:

Because these position and momentum variables are continuous-valued, the probability of actually landing back in the starting state has measure zero.

Suppose, however, that after we integrate for \(L\) steps, we flip the sign of the momentum term. Then we have

\[\mathbb{Q}(q',p' \mid q_0,p_0) = \delta(q'-q_L) \delta(p'+p_L)\]

so that only \((q',p')=(q_L,-p_L)\) results in a probability mass of one. See the following figure for this revision:

The key observation now, of course, is that

\[\mathbb{Q}(q_0,p_0 \mid q_L,-p_L) = 1\]

Why is this true? The dynamics are time-reversible, and if we set our potential energy to be the usual \(K(p) = \frac{p^Tp}{2}\), then flipping the momentum term and going through the leapfrog means the sampler encounters the same exact steps, only in reverse.

To make this concrete, I like to explicitly go through the math of one leapfrog step. It requires some care with notation, but I find it’s worth it. I’ll write \((q_k^{(1)},p_k^{(1)})\) as the \(k\)-th element encountered during the forward trajectory. For the reverse, I use \((q_k^{(2)},p_k^{(2)})\) so that the superscript is now two instead of one. Furthermore, due to the leapfrog step taking half-steps for momentums, I use \(k=0.5\) for this purpose.

Here’s the forward trajectory, starting from \((q_0^{(1)},p_0^{(1)})\):

\[\begin{align} p_{0.5}^{(1)} &= p_0^{(1)} - \frac{\epsilon}{2}\nabla U(q_0^{(1)}) \\ q_{1}^{(1)} &= q_0^{(1)} + \epsilon p_{0.5}^{(1)} \\ p_{1}^{(1)} &= p_{0.5}^{(1)} - \frac{\epsilon}{2}\nabla U(q_1^{(1)}) \end{align}\]

and the last step negates the momentum, so that the final state is \((q_1^{(1)}, -p_1^{(1)})\).

Here’s the reverse trajectory, starting from \((q_0^{(2)},p_0^{(2)})\):

\[\begin{align} p_{0.5}^{(2)} &= p_0^{(2)} - \frac{\epsilon}{2}\nabla U(q_0^{(2)}) \\ q_{1}^{(2)} &= q_0^{(2)} + \epsilon p_{0.5}^{(2)} \\ p_{1}^{(2)} &= p_{0.5}^{(2)} - \frac{\epsilon}{2}\nabla U(q_1^{(2)}) \end{align}\]

with our final state as \((q_1^{(2)}, -p_1^{(2)})\). Above, the only difference between the reverse and the forward trajectories is the change in superscripts. But when we do the math for the reverse trajectory while plugging in the values from the forward trajectory, we get:

\[\begin{align} p_{0.5}^{(2)} &= p_0^{(2)} - \frac{\epsilon}{2}\nabla U(q_0^{(2)}) \\ &= -p_1^{(1)} - \frac{\epsilon}{2}\nabla U(q_1^{(1)}) \\ &= -\left(p_{0.5}^{(1)} - \frac{\epsilon}{2}\nabla U(q_1^{(1)})\right) - \frac{\epsilon}{2}\nabla U(q_1^{(1)}) \\ &= -p_{0.5}^{(1)} \end{align}\]

Gee, this is exactly the negative of the half-step we were at in the first iteration! Similarly, for the position update, we have:

\[\begin{align} q_{1}^{(2)} &= q_0^{(2)} + \epsilon p_{0.5}^{(2)} \\ &= q_1^{(1)} - \epsilon p_{0.5}^{(1)} \\ &= q_0^{(1)} + \epsilon p_{0.5}^{(1)}- \epsilon p_{0.5}^{(1)} \\ &= q_{0}^{(1)} \end{align}\]

The leapfrog has brought the position back to the starting point. For the final half-step momentum update, we have:

\[\begin{align} p_{1}^{(2)} &= p_{0.5}^{(2)} - \frac{\epsilon}{2}\nabla U(q_1^{(2)}) \\ &= -p_{0.5}^{(1)} - \frac{\epsilon}{2}\nabla U(q_0^{(1)}) \\ &= -\left(p_{0}^{(1)} - \frac{\epsilon}{2}\nabla U(q_0^{(1)})\right) - \frac{\epsilon}{2}\nabla U(q_0^{(1)}) \\ &= -p_{0}^{(1)} \end{align}\]

and we see that our reverse trajectory landed us back in \((q_0^{(1)},-p_0^{(1)})\), and flipping the momentum gets us to the same exact starting state.

Thus, using this type of proposal means the proposal densities cancel out, result in a Metropolis test, not a Metropolis-Hastings test.

I should also add one other point: we do not consider the momentum resampling as being part of the proposal, as resampling the momentum can be considered as maintaining the canonical distribution, so it’s something that we can “always” decide to invoke if we want (hopefully that’s not too bad of a hand-wavy explanation).

Hopefully the above discussion clarifies why flipping the sign of the momentum is necessary, at least in theory. In practice, we don’t do it since for the usual Gaussian kinetic energies, \(K(p) = K(-p)\) so their energy levels are the same, and because the momentum variables are traditionally entirely resampled after the acceptance test.

This semester, I took CS 294-131, a Deep Learning “special topics” course which has been offered each semester since Fall 2016 for a variable amount of class units and will be taught again next semester (the course website is already up). As usual, it was co-taught by the Trevor Darrell and Dawn Song team. The course is low-commitment for them because it’s a seminar and they don’t have to give lectures or prepare assignments and exams. CS 294-131 meets only once a week; for us, it was Mondays from 1:00PM to 2:30PM. Each meeting featured a guest speaker from academia or industry who gave a talk on his or her cutting-edge Deep Learning research results.

Here were some of the highlights for me:

• Vladlen Koltun’s talk about his ICLR 2017 paper Learning to Act by Predicting the Future. I enjoyed his presentation, though admittedly most of it was because he was funny and actively engaging with the audience. I previously blogged about the more technical aspects here.

• Barret Zoph and Quoc Le’s joint talk on neural architecture search, also from ICLR 2017 (here’s the OpenReview link) and also (like Koltun’s paper) an oral presentation at that conference. I’ve been hoping to find some time to read their paper and perhaps the winter break will afford me that opportunity. Zoph and Le’s presentation featured a lot of aggressive questioning from students, to the point where Professor Song asked the students to quiet down and let the speakers proceed. Fortunately, at least to me, the technical content of the presentation was interesting enough to keep my attention.

• Ross Girshik’s talk on computer vision and object recognition. Actually, we had a fire alarm for this one, which delayed the start class for about 15 minutes … so then we had to find a new room. Unfortunately, it took about 10 more minutes to get the projector working, and then we were told we had to leave the room at around 2:10PM. At least when Girshik was actually able to talk about computer vision, I found the historical overview to be educational.

• Percy Liang’s presentation on fighting black boxes and adversaries in Deep Learning. This was somewhat more theoretical work but he didn’t go too much into the details. I am less familiar with his work but would like to get accustomed with it as adversarial learning is a pretty hot topic in robotics these days.

In case you’re wondering, yes I had the usual sign language interpreters for the class. Yes they were unhappy, but they tried, and we were able to agree on a few terminology-related issues beforehand. And yes, I didn’t get all the technical details from the talks. I tried to allocate two hours before class to do the background reading, but inevitably that turned into 1.5 hours … and then 1 hour … and then 30 minutes. How do people manage to do class readings ahead of time when they’re juggling four major research projects? Or do people with normal hearing just find it easy to absorb almost all the technical stuff in these talks without prior preparation?¹

As I mentioned earlier, CS 294-131 can be taken for a different amount of credits. This year, we had the option of taking it for 1, 2, or 3 credits. We got one credit for doing “arXiv summaries” and “discussion leads” and two for doing a class project. I decided that those summaries and discussions would be too much of a hassle, so I took CS 294-131 for two credits. It helps that I’ve long since finished my course requirements.

While I enjoyed some of the Deep Learning talks, I do have some criticisms about CS 294-131:

• There are too many websites/links related to the class. We have Piazza, the course website, the Google group (seriously?) and Slack channels, with one for each new week. I think this is too much information and things should be centralized in two spots at most — the course website and Piazza.

• I’m also not a fan of the arXiv leads, which was new this semester. Students had to give 1-minute presentations on Deep Learning papers that appeared on arXiv the past week. The problem with this is that the majority of students tried to cram as may technical details in their talk as possible, rather than give the clear key insight from the paper. In addition, students often went over their allotted speaking time (gee, who would have guessed??).

• Finally, I have no idea why class participation is worth 20% of the grading here. On Piazza, we were literally told that we would get class participation credit by simply attending the lectures. Not only does it not make sense to award students who attend lectures but don’t pay attention, it also hurts those who watch the video livestreams to reduce pressure on the lecture room, since the first lecture was “standing-room only.”

To be honest, I didn’t quite enjoy the class as much as I should have, and my project didn’t turn out as well as I would have liked. I worked on a Deep Reinforcement Learning project with three other students, and hopefully that will turn into a research paper later, but in retrospect, it’s difficult to coordinate a four-person project when everyone else has other priorities.

I don’t plan to take the Spring 2018 version of the course, but I’ll certainly keep track of the papers in the background reading. I’m excited to see who the guest speakers will be this time around …

---