CS Theory Part 1 of 8: Finite Automata

As I mentioned before, I am writing a series of blog posts on my Theory of Computation class. This particular post will be somewhat image-heavy due to complete lack of experience on how to use LaTeX in accordance with state machine diagrams. Even the LaTeX I embed in these posts doesn’t look too great with this background, so I’ll have to do some more experiments. UPDATE May 16, 2015: I think the Jekyll + MathJax combination looks great now!

But anyway, in this class, I’m trying to understand three central areas: automata, computability, and complexity, and they are all linked by the following question:

What are the fundamental capabilities and limitations of computers?

Computability and complexity will come later in the course. Right now we’re focusing on automata.

To start off, let’s look at some basic computers, called finite automata. To put things formally, a finite automaton is a 5-tuple \((Q, \sum, \delta, q_{1}, F)\), where¹

1. \(Q\) is a finite set of states
2. \(\sigma\) is a finite set known as the alphabet
3. \(\delta: Q \times \sigma \longrightarrow Q\) is the transition function
4. \(q_{1} \in Q\) is the start state
5. \(F \subset Q\) is the set of accept states

But this is very abstract. Let’s get more specific by talking about the alphabet, and I’ll then return to discuss the other four points. An alphabet is defined to be any nonempty, finite set of symbols. For instance, \(\sum = \{0,1\}\) is a valid alphabet. And so is the alphabet composed of the 26 letters of the English language.

Related to alphabets, we have strings and languages. A string is just a finite sequence of characters derived from our alphabet. All the English words I type in this blog entry are strings of the alphabet composed of the 26 letters of the English language. The sequence of symbols in 11001100 is a valid string of the alphabet \(\sum = \{0,1\}\). Any binary number is a string that can be formed by the alphabet. And a language is a set of these strings.

Here is the key relation between languages and finite automata.

A language is called a regular language if some finite automaton recognizes it.

By definition, a finite automaton will recognize a language if all strings the automaton accepts are members of the language. That’s the key. And to indicate what I mean, let’s look at a state diagram. Many finite automata can be written using these diagrams, and it’s highly advantageous to do so given how intuitive it is. The following is a state diagram of a finite automata that recognizes some language.

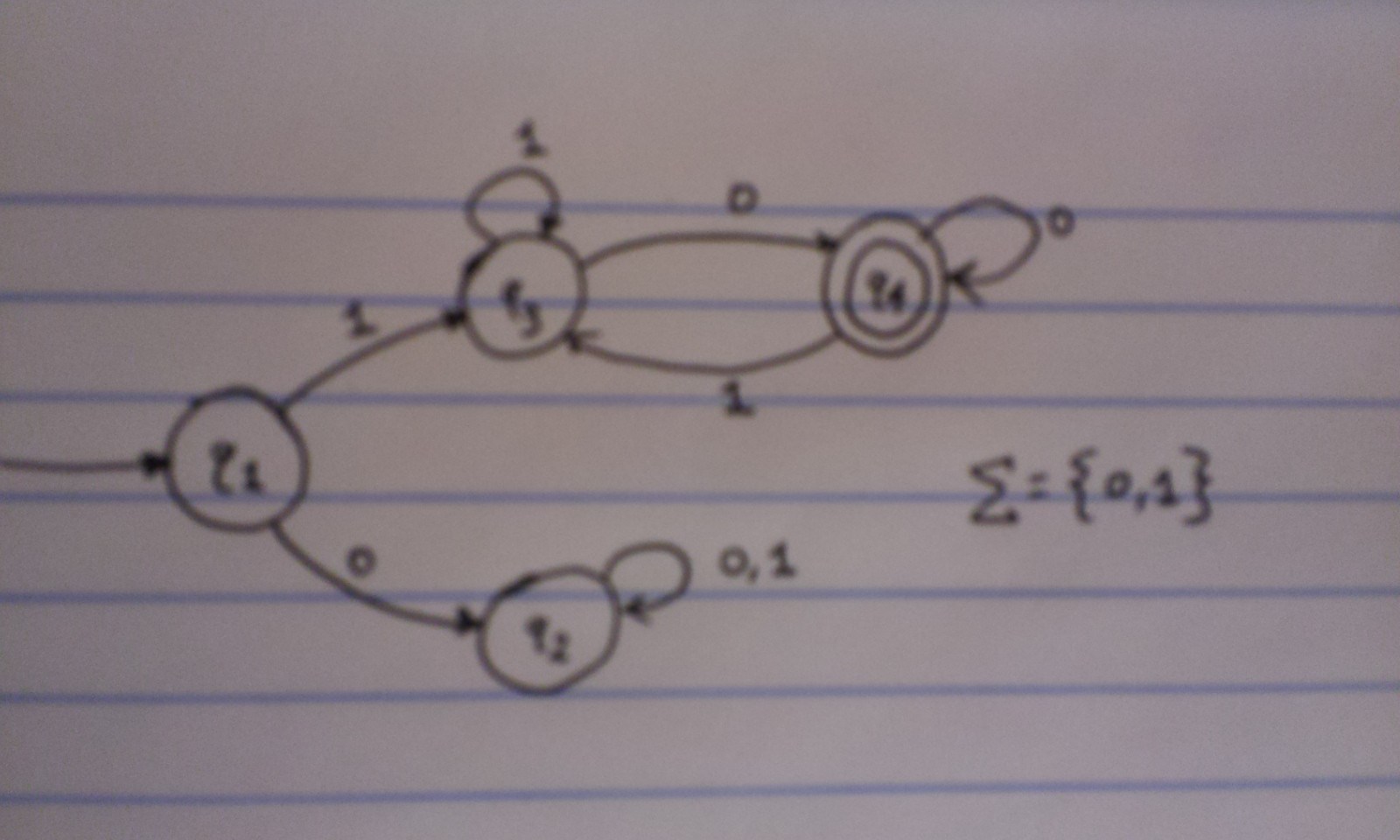
It’s a little blurry (future images will be better), but I hope you can still see the interesting symbols. First, there are four large circles, with one having a circle within it. Each of these four circles represents a state. Hence, \(\{q_{1}, q_{2}, q_{3}, q_{4}\} = Q\), the set of states (#1 on my list above). These are used to represent some situation that we encounter as we progress through a given string.

We have \(q_{1}\) forming our *start state *(#4 on my list above). This means when we progress through a given string, this is where we start before we make any “moves.” And \(q_{4}\) represents the lone accept state, indicated by the double circle outline. We can have multiple — or zero — accept states; this particular diagram only has one. If a string ends on one of these states, it’s “accepted” by the language. Otherwise, it’s rejected.

When I say “progress through a given string,” I refer to the process of determining whether a machine will recognize a certain string, and here is where we use the transition function (#3 on my list above), indicated by arrows in the diagram. Our alphabet in the above example is composed of just 0 and 1, so the machine only works with strings of that form. Let’s see what happens when we “input” a few strings into this machine.

1. \(\varepsilon\) — This is the empty string. We start by going to \(q_{1}\) and we stop there, since we have no characters left. The finish state is the same as the start state, but this means the empty string is not accepted by the language since it did not finish in state \(q_{4}\).
2. “1” — Here, we again start at the empty state. From this point forth, always assume we start at the start state. Since we have a “1” this means we go to state \(q_{3}\) as dictated by the transition function (i.e. arrows). We stop here, because we’re out of characters. But unfortunately, “1” did not end in the accept state so, like \(\varepsilon\), it is not accepted by the machine.
3. “0” — We go from the start state to \(q_{2}\). Again, we stop, and just as in the previous two examples, the machine doesn’t accept the string.
4. By now it should be clearer what should be accepted by the machine. Let’s go with “10” and see what happens. We start at \(q_{1}\) as usual.  We proceed to \(q_{3}\) since we started with a 1. Our next character is a 0, so we go to \(q_{4}\) and stop there. At last! We have a string that is recognized by the language! So whatever the language is here, it better include “10” but exclude “1”, “0”, and the empty string.
5. Let’s try “010”. We start by going to \(q_{2}\) due to the leading zero. Then we have “10” left, so we follow the arrow for the “1” which loops back to the same state. Then our final task is to go where the “0” arrow points to, but again, that goes back to the same \(q_{2}\) state! Thus, “010” is not accepted by this machine.

We can go on and on, but at some point, we have to come up with the rules for this language the machine accepts. Notice that state \(q_{2}\) is a “death” or “trap” state, because as soon as a string enters that state, it must end there. All strings are finite, and no matter what, any symbol we get (which is only a 0 or a 1 here) will lead us back to the same state. In other words, it is impossible for a string to be accepted (i.e. finish at \(q_{4}\)) if it ever enters \(q_{2}\). This means that if a string has a leading zero, it will never be accepted by the language/machine.

So now we know the language this machine recognizes must have all strings starting with a 1. But are there further restrictions? The answer is yes. If we have a string that consists of all 1s, then we will always end at \(q_{3}\) due to the 1 that loops back to that state. This is not an accept state, so we need to consider having a 0 in some string. Notice that the accept state has a 0 that loops back to it. So if a given string ever reaches \(q_{4}\), as long as it ends in a 0, it will remain in that state and be accepted. It doesn’t matter if we have one, five, or a hundred zeroes. The only way a string can leave an accept state is by having a 1, which means that string goes back to \(q_{3}\). But notice that this is not a death state! It is possible to come back to the accept state if a string is in \(q_{3}\).

Now we can formalize things. This state machine recognizes the following language \(L\):

And we know that this language is regular. (To show a language is regular, it suffices to make a state diagram of a finite automaton.)

It’s also worth pointing out that the diagram I have above should represent the simplest possible state machine that accepts this language. There are infinitely many other diagrams that would also accept this language.

Now that was a simple example. I want to bring up a more complicated question that uses these same concepts.

Interesting Question

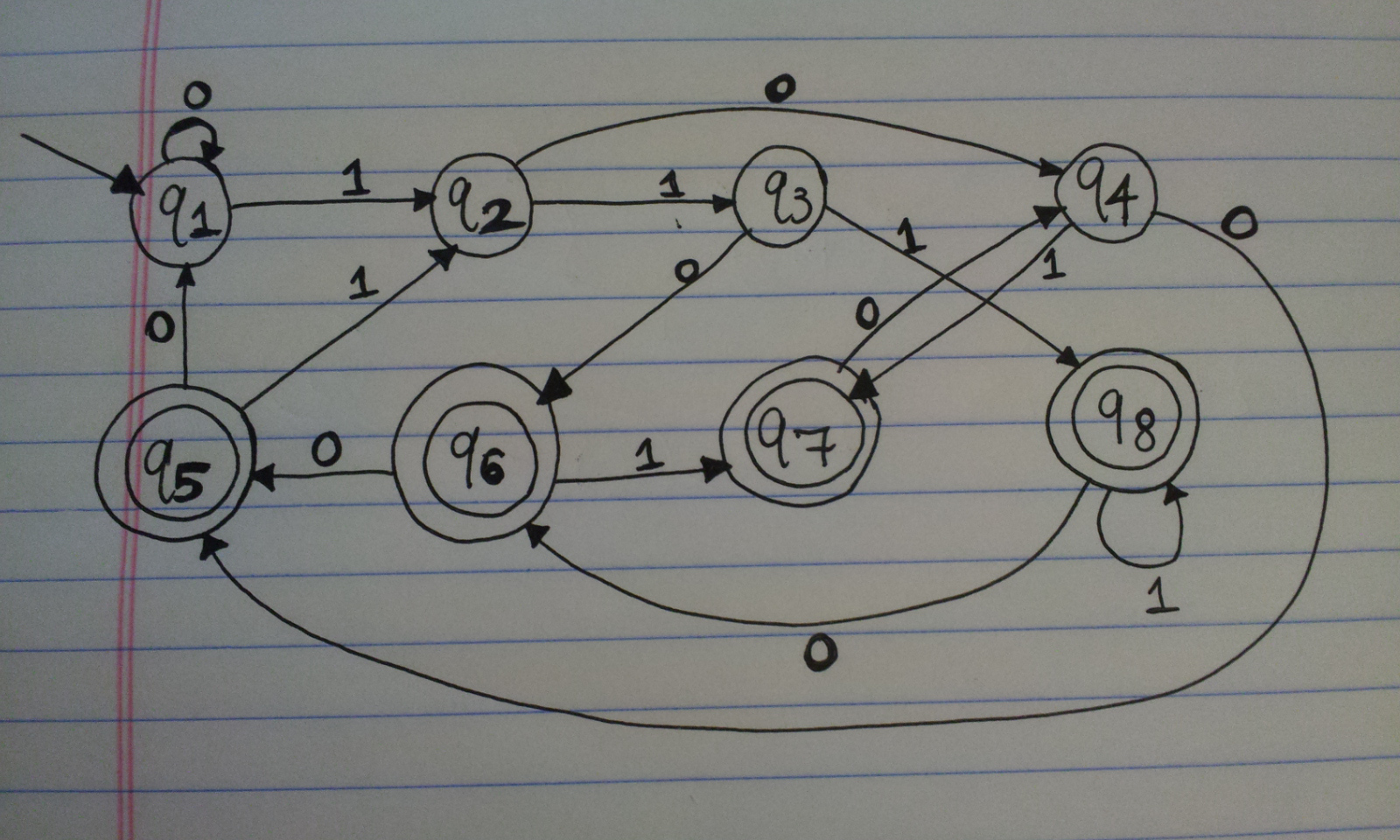
Let \(A\) be the language consisting of all strings over \(\{0,1\}\)  containing a 1 in the third position from the end.

Designing a finite automata that accepts some language is arguably harder than the reverse process, determining what language is accepted by a given machine. I have my solution to the above question below. The diagram only needs to keep track of the last three digits. There are four accept states that correspond to the last three digits being 100, 101, 110, or 111, which are the four possibilities we could have for the last three symbols of accepted strings. Naturally, the four other non-accept states correspond to the last three symbols being 000, 001, 010, or 011.

Up to now, I assumed that my finite automaton were deterministic, so it was always possible to know what was happening. But soon I’ll be moving on to non-deterministic finite automaton …