CS Theory Part 3 of 8: Context-Free Grammars
(Note: I’m aware that I’ve been a bit computer science heavy in the past month; I’m working on getting additional topics up here, but time is scarce, and I may end up revising these posts a bit in the winter.)
We’re moving on to the next unit of Theory of Computation, which deals with context-free languages. These are a special class of languages that contain the regular languages, but a few other non-regular ones. (See CS Theory Part 2 for ways in which I prove certain languages are not regular.) What makes them different as compared with regular languages is that languages are context-free if we can derive a context-free grammar that describes it. A grammar is simply a way of constructing strings using a set of terminals and variables. Consider the example below.
\[S \longrightarrow T1T \\ T \longrightarrow TT \mid 0T1 \mid 1T0 \mid 1 \mid \varepsilon\]This grammar will generate the language containing all strings that have more 1s than 0s, assuming the entire alphabet is composed of just 0 and 1.
Clearly, using grammars to generate languages is more powerful than regular expressions, because of the ability to generate non-regular languages. To derive any string from the language, we start with the variable \(S\), which generates a required 1; this is necessary because in order for a string to have more 1s than 0s, we must have at least one 1 as the string “1” is clearly in the language. But \(S\) generates another variable with that 1, which we call \(T\). This \(T\) can recursively expand to generate an infinite number of strings. For each derivation, we substitute the \(T\) with a randomly chosen derivation, such as \(0T1\). The derivation process ends when we have all non-terminals (i.e. 0s and 1s), and the resulting string formed will be a member of the language. The language described above is non-regular because any DFA recognizing it would have to keep track of how many 0s and 1s there were, and there could be infinitely many of them.
I now want to introduce a new finite automaton called pushdown automata, These are analogous to NFAs in that constructing a pushdown automata (PDA) that recognizes a given language is the same as showing that the language is context-free. Thus, to show a language is context-free, either (1) construct a context-free grammar generating it, or (2) construct a PDA recognizing it.
The main difference between NFAs and PDAs is the stack component of the PDA, which is empty at the start of an input string but can have alphabet symbols (e.g. a 0 or a 1) or arbitrary symbols added as the input string is read. This is the heart of why context-free languages are a super set of the regular languages; an NFA is a PDA, but a PDA provides additional counting and memory capabilities, which allows languages, such as the canonical non-regular language of \(\{0^n1^n \mid n \ge 0\}\), to be considered context-free. Like NFAs, we can easily draw PDAs to recognize languages using states and transition arrows. This time, when making a transition arrow, we use symbols of the form \(a, b \longrightarrow c\). This is saying “if we read in \(a\) as input, we may pop \(b\) off the top of the stack and add on \(c\)”. Note: if the symbol on the top of the stack doesn’t match the transition function, that computational path dies. Furthermore, \(\varepsilon\) can be used anywhere in the transition function, as we’ll see in the always-necessary example later.
Example PDA
What language do you think this PDA recognizes? Note: the dollar sign is added on the stack before the first character is read; it’s used solely to indicate the bottom of the stack.
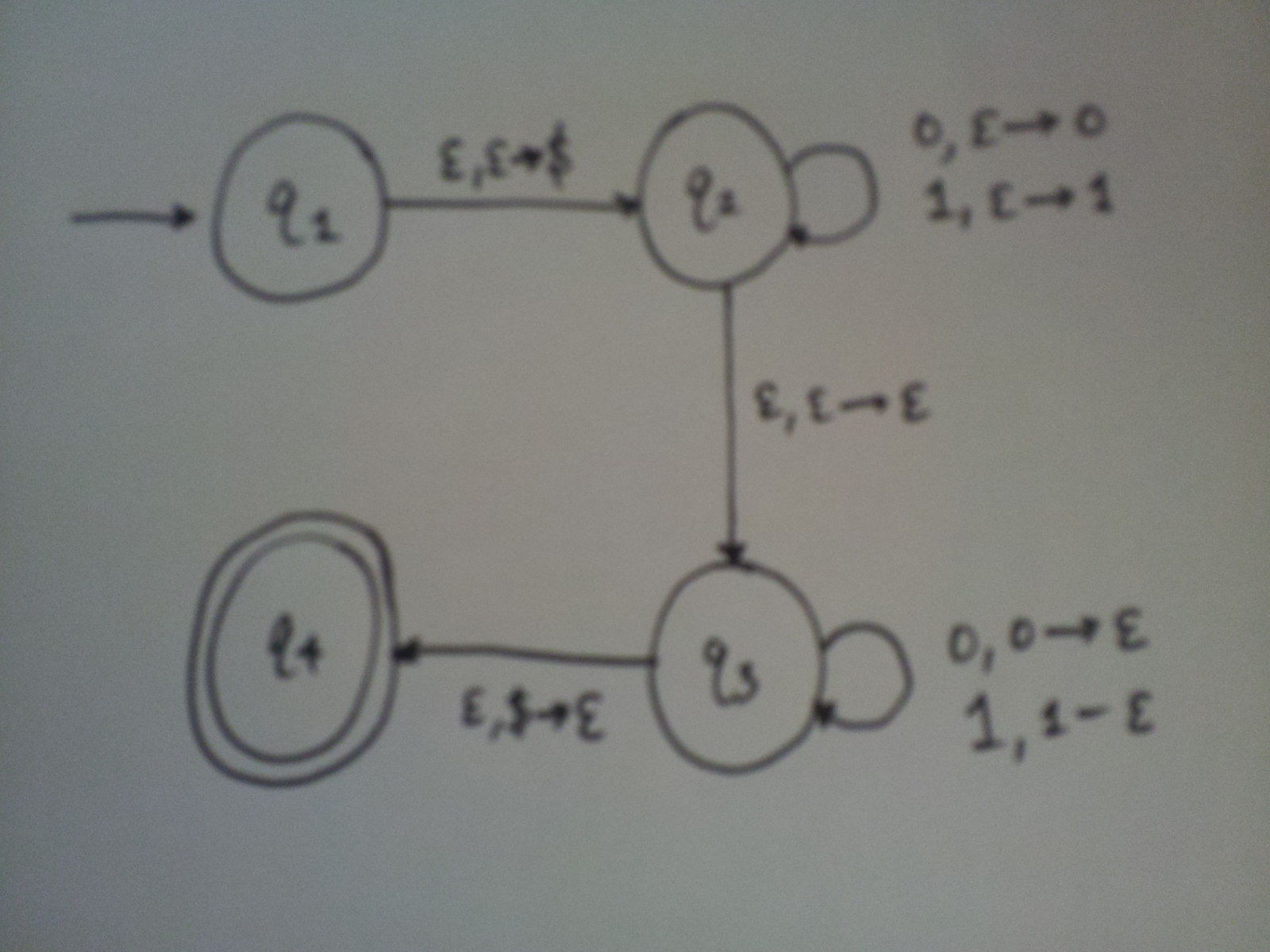
The above PDA will accept all strings that recognize the language \(\{ww^R \mid w \in \{0,1\}^* \}\). It nondeterministically guesses where the middle of the input string will be, and tries to pop off stuff from the stack from that point on. Since we have nondeterminism here, we are guaranteed that if a string is in the language previously described, then it will be recognized by this PDA. Pretty impressive! Notice that this language is non-regular, which we can justify with a simple pumping lemma proof.
Up next for me is arguably the most important concept of the course: the Turing Machine.