Learning to Poke by Poking: Experiental Learning of Intuitive Physics
One of the things I’m most excited about nowadays is that physical robots now have the capability to repeatedly execute trajectories to gather data. This can then be fed into a learning algorithm to subsequently learn complex manipulation tasks. In this post, I’ll talk about a paper which does exactly that: the NIPS 2016 paper Learning to Poke by Poking: Experiental Learning of Intuitive Physics. (arXiv link; project website) Yes, it’s experiental, not experimental, which I originally thought was a typo, heh.
The main idea of the paper is that by repeatedly poking objects, a robot can then “learn” (via Deep Learning) an internal model of physics. The motivation for the paper came out of how humans seem to possess this “internal physics” stuff:
Humans can effortlessly manipulate previously unseen objects in novel ways. For example, if a hammer is not available, a human might use a piece of rock or back of a screwdriver to hit a nail. What enables humans to easily perform such tasks that machines struggle with? One possibility is that humans possess an internal model of physics (i.e. “intuitive physics” (Michotte, 1963; McCloskey, 1983)) that allows them to reason about physical properties of objects and forecast their dynamics under the effect of applied forces.
I think it’s a bit risky to try and invoke human reasoning in a NIPS paper, but it seems to have worked out here (and the paper has been cited a fair amount).
The methodology can be summarized as:
In our setup (see Figure 1), a Baxter robot interacts with objects kept on a table in front of it by randomly poking them. The robot records the visual state of the world before and after it executes a poke in order to learn a mapping between its actions and the accompanying change in visual state caused by object motion. To date our robot has interacted with objects for more than 400 hours and in process collected more than 100K pokes on 16 distinct objects.
Now, how does the Deep Learning stuff work to actually develop this internal model? To describe this, we need to understand two things: the data collection and the neural network architecture(s).
First, for data collection, they randomly poke objects in a workstation and collect the tuple of: before image, after image, and poke. The first two are just the images from the robot sensors and the “poke” is a tuple with information about the poke point, direction and length. Second, they train two models: a forward model to predict the next state given the current state and the applied force, and an inverse model to predict the action given the initial and target state. A state, incidentally, could be the raw image from the robot’s sensors, or it could be some processed version of it.
I’d like to go through the architecture in more detail. If we assume naively that the forward and inverse models are trained separately, we get something like this:
Visualization of the forward and inverse models. Here, we assume the forward and
inverse models are trained separately. Thus, the forward model takes a raw image
and action as input, and has to predict the full image of the next state. In the
inverse model, the start and goal images are input, and it needs to predict the
action that takes the environment to the goal image.
where the two models are trained separately and act on raw images from the robot’s sensors (perhaps 1080x1080 pixels).
Unfortunately, this kind of model has a number of issues:
- In the forward model, predicting a full image is very challenging. It is also not what we want. Our goal is for forward model to predict a more abstract event. To use their example, we want to predict that pushing a glass over a counter will result in the abstract event of “shattered glass.” We don’t need to know the precise pixel location of every shattered glass.
- The inverse model has to deal with ambiguity: there are multiple actions that may head to a resulting goal state, or perhaps no action at all can possibly lead to the next state.
All these factors require some re-thinking in terms of our model architecture (and training protocol). One obvious alternative the authors suggest is to avoid acting on image space and just feed all images into a CNN trained on ImageNet data and extract some intermediate layer. The problem is that it’s unclear if object classification and object manipulation mandate a similar set of features. One would also need to fine-tune ImageNet somehow, which would make this more task-specific (e.g., for a different workstation setup, you’d need to fine-tune again).
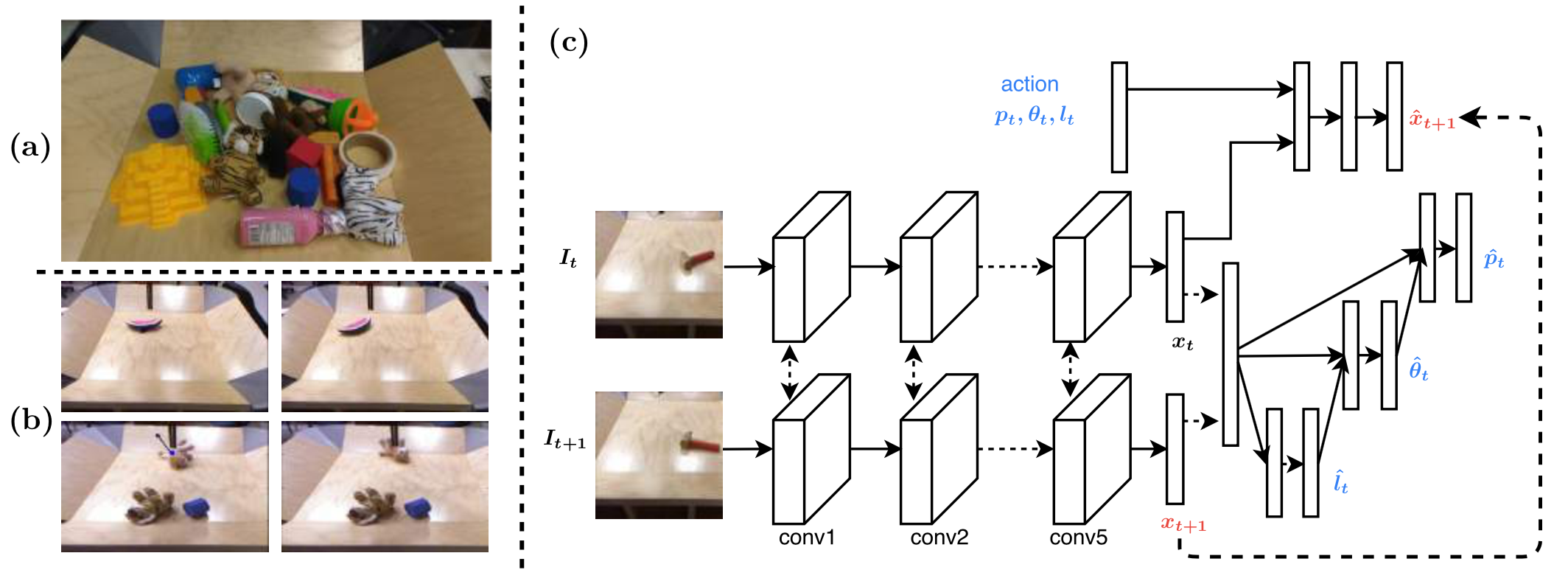
Figure from their paper describing (a) objects used, (b) before/after image
pairs, (c) the network.
Their solution, shown above, involves the following:
-
Two consecutive images \(I_t, I_{t+1}\) are separately passed through a CNN and then the output \(x_t, x_{t+1}\) (i.e., latent feature representation) is concatenated.
-
To conclude the inverse model, \((x_t, x_{t+1})\) are used to conditionally estimate the poke length, poke angle, and then poke location. We can measure the prediction accuracy since all the relevant information was automatically collected in the training data.
As to why we need to predict conditionally: I’m assuming it’s so that we can get “more reasonable” metrics since knowing the poke length may adjust the angle required, etc., but I’m not sure. (The project website actually shows a network which doesn’t rely on this conditioning … well OK, it’s probably not a huge factor.) Update 03/29/2018: actually, it’s probably because it reduces the number of trainable weights.
Also, the three poke attributes are technically continuous, but the authors simply discretize.
-
For the forward model, the action \((p_t, \theta_t, l_t)\) along with the latent feature representation \(x_t\) of image \(I_t\) is concatenated and fed through its own neural network, to predict \(x_{t+1}\), which in fact we already know as we have passed it through the inverse model!
By integrating both networks together, and making use of the randomly-generated training data to provide labels for both the forward and inverse model, they can simply rely on one loss function to train:
\[L_{\rm joint} = L_{\rm inv}(u_t, \hat{u}_t, W) + \lambda L_{\rm fwd}(x_{t+1}, \hat{x}_{t+1}, W)\]where \(\lambda > 0\) is a hyperparameter. They show that using the forward model is better than ignoring it by setting \(\lambda = 0\), so that it is advantageous to simultaneously learn the task feature space and forecasting the outcome of actions.
To evaluate their model, they supply their robot with a goal image \(I_g\) and ask it to apply the necessary pokes to reach the goal from the current starting state \(I_0\). This by itself isn’t enough: what if \(I_0\) and \(I_g\) are almost exact the same? To make results more convincing, the authors:
- set \(I_0\) and \(I_g\) to be sufficiently different in terms of pixels, thus requiring a sequence of pokes.
- use novel objects not seen in the (automatically-generated) training data.
- test different styles of pokes for different objects.
- compare against a baseline of a “blob model” which uses a template-based object detector and then uses the vector difference to compute the poke.
One question I have pertains to their greedy planner. They claim they can provide the goal image \(I_g\) into the learned model, so that the greedy planner sees input \((I_t,I_g)\) to execute a poke, then sees the subsequent input \((I_{t+1},I_g)\) for the next poke, and so on. But wasn’t the learned model trained on consecutive images \((I_t,I_{t+1})\) instead of \((I_t,I_g)\) pairs?
The results are impressive, showing that the robot is successfully able to learn a variety of pokes even with this greedy planner. One possible caveat is that their blob baseline seems to be just as good (if not better due to lower variance) than the joint model when poking/pushing objects that are far apart.
Their strategy of combining networks and conducting self-supervised learning with large-scale, near-automatic data collection is increasingly common in Deep Learning and Robotics research, and I’ll keep this in mind for my current and future projects. I’ll also keep in mind their comments regarding generalization: many real and simulated robots are trained to achieve a specific goal, but they don’t really develop an underlying physics model that can generalize. This work is one step in the direction of improved generalization.