The virtual Robotics: Science and Systems (RSS) conference will happen in about a week, and I will be presenting a paper there. This is going to be my first time at RSS, and I was hoping to go to Oregon State University and meet other researchers in person, but alas, given the rapid disintegration of America as it pertains to COVID-19, a virtual meeting makes 100 percent sense. For RSS 2020, I’ll be presenting our paper VisuoSpatial Foresight for Multi-Step, Multi-Task Fabric Manipulation, co-authored with Master’s (and soon to be PhD!) student Ryan Hoque. This is based on a technique called visual foresight, and in this blog post, I’d like to briefly touch upon the technique, and then discuss a little more about our RSS 2020 paper, along with another surprising paper which shows that perhaps we need to rethink our deep models.

First, to make sure we’re on common ground here, what do people mean when we say the words “Visual Foresight”? This refers to the technique described in an ICRA 2017 paper by Chelsea Finn and Sergey Levine, which was later expanded upon in a longer journal paper with lead authors Chelsea Finn and Frederik Ebert. The authors are (or were) at UC Berkeley, my home institution, which is one reason why I learned about the technique.

Visual Foresight is typically used in a model-based RL framework. I personally categorize model-based methods into whether the models predict images or whether they predict some latent variables (assuming, of course, that the model itself needs to be learned). Visual Foresight applies to the former case for predicting images. In practice, given the difficult nature of image prediction, this is often done by predicting translations or deltas between images. For the second case of latent variable prediction, I refer you to the impressive PlaNet research from Google.

For another perspective on model-based methods, the following text is included in OpenAI’s “Spinning Up” guide for deep reinforcement learning:

Algorithms which use a model are called model-based methods, and those that don’t are called model-free. While model-free methods forego the potential gains in sample efficiency from using a model, they tend to be easier to implement and tune. As of the time of writing this introduction (September 2018), model-free methods are more popular and have been more extensively developed and tested than model-based methods.

and later:

Unlike model-free RL, there aren’t a small number of easy-to-define clusters of methods for model-based RL: there are many orthogonal ways of using models. We’ll give a few examples, but the list is far from exhaustive. In each case, the model may either be given or learned.

I am writing this in July 2020, and I believe that since September 2018, model-based methods have made enormous strides, to the point where I’m thinking that 2018-2020 might be known as the “model-based reinforcement learning” era. Also, to comment on a point from OpenAI’s text, while model-free methods might be easier to implement in theory, I argue that model-based methods can be far easier to debug, because we can check the predictions of the learned model. In fact, that’s one of the reasons why we took the model-based RL route in our RSS paper.

Anyway, in our RSS paper, we focused on the problem of deformable fabric manipulation. In particular, given a goal image of a fabric in any configuration, can we train a pick-and-place action policy that will manipulate the fabric from an arbitrary starting configuration to the goal configuration? For Visual Foresight, we trained a deep recurrent neural network model that could predict full 56x56 resolution images of fabric. We predicted depth images in addition to color images, making the model “VisuoSpatial.” Specifically, we used Stochastic Variational Video Prediction (SV2P) as our model. The wording “Stochastic Variational” means the model samples a latent variable before generating images, and the stochastic nature of that variable means the model is not deterministic. This is an important design aspect; see the SV2P paper for further details. But, as you might imagine, this is a very deep, recurrent, and complex model. Is all this complexity needed?

Perhaps not! In a paper at the Workshop on Algorithmic Foundations of Robotics (WAFR) this year, Terry Suh and Russ Tedrake of MIT show that, in fact, linear models can be effective in Visual Foresight.

Wait, really?

Let’s dive into that work in more detail, and see how it contrasts to our paper. I believe there are great insights to be gained from reading the WAFR paper.

In this paper, Terry Suh and Russ Tedrake focus on the task of pushing small objects into a target zone, such as pushing diced onions or carrots not unlike how a human chef might need do so. Their goal is to train a pushing policy that can learn and act based on greyscale images. They make a similar argument that we do in our RSS 2020 paper about the difficulty of knowing the “underlying physical state.” For us, “state” means vertices of cloth. For them, “state” means knowing all poses of objects. Since that’s hard with all these small objects piled upon each other, learning from images is likely easier.

The actions are 4D vectors $\mathbf{u}$ which have (a) the 2D starting coordinates, (b) the scalar push orientation, and (c) the scalar push length. They use Pymunk for simulation, which I’ve never heard of before. That’s odd, why not use PyBullet, which might be more standardized for robotics? I have explicitly been able to simulate this kind of environment in PyBullet.

That having been said, let’s consider first how (a) they determine actions, and (b) their visual foresight video prediction model.

Section 2.2 describes how they pick actions (for all methods they benchmark). Unlike us, they do not use the Cross Entropy Method (CEM) — there is no action sampling plus distribution refitting as happens in the CEM. The reason is that they can define a Lyapunov function which accurately characterizes performance on their task, and furthermore, they can minimize for it to get a desired action. The Lyapunov function $V$ is defined as:

\[V(\mathcal{X}) = \frac{1}{|\mathcal{X}|} \sum_{p_i \in \mathcal{X}} \min_{p_j \in \mathcal{S}_d} \|p_i - p_j\|_{p}\]

where \(\mathcal{X} = \{p_i\}\) is the set of all 2D particle positions, and $\mathcal{S}_d$ is the desired target set for the particles. The notation \(\| \cdot \|_p\) simply refers to a distance metric in the $p$-norm.


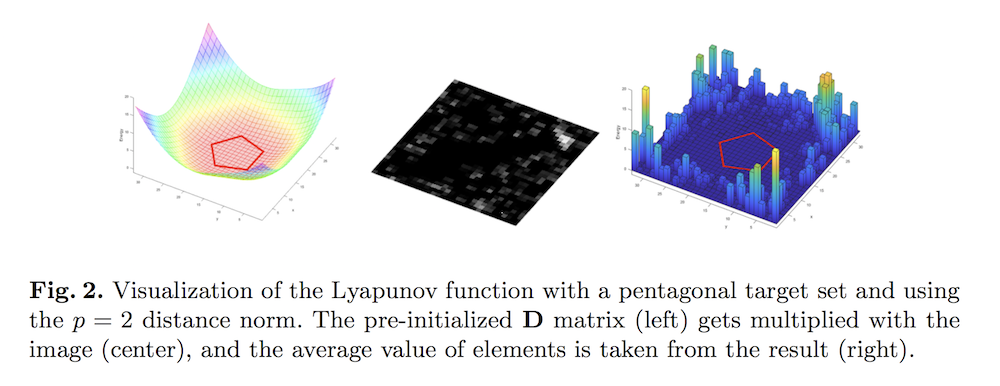
The figure above is from the paper, who visualizes the Lyapunov function. It is interpreted as a distance between a discrete set of points and a continuous target set. There’s a pentagon at the center indicating the target set. In their instantiation of the Lyapunov function, if all non-zero pixels (nonzero means carrots, due to height thresholding) in the image of the scene coincide with the pentagon, then the element-wise product of the two images is 0 everywhere, and summing it all will result in 0.

The paper makes the assumption that:

for every image that is not in the target set, we can always find a small particle to push towards the target set and decrease the value of the Lyapunov function.

I agree. While there are cases when pushing particles inwards might result in higher values (i.e., worse performance) due to pushing particles inside the zone to be outside of it, I think it is always possible to find some movement that gets a greater number of particles in the target. If anyone has a counter-example, feel free to share. This assumption may be more true for convex target sets, but I don’t think the authors make that assumption since they test on targets shaped “M”, “I”, and “T” later.

Overall, the controller appears to be accurate enough so that the prediction model performance is the main bottleneck. So which is better: deep or switched-linear? Let’s now turn to that, along with the “visual foresight” aspect of the paper.

Their linear model is “switched-linear”. This is an image-to-image mapping based on a linear map characterized by

\[y_{k+1} = \mathbf{A}_i y_k\]

for \(i \in \{1, 2, \ldots, |\mathcal{U}|\}\), where $\mathcal{U}$ is the discretized action space and $y_k \in \mathbb{R}^{N^2}$ represents the flattened $N \times N$ image at time $k$. Furthermore, $\mathbf{A}_i \in \mathbb{R}^{N^2 \times N^2}$. This is a huge matrix, and there are as many of these matrices as there are actions! This appears to require a lot of storage.

My first question after reading this was: when they train the model using pairs of current and successor images $(y_{k}, y_{k+1})$, is it possible to train all the $\mathbf{A}_i$ matrices?

Or are we restricted to only the matrix corresponding to the action that was chosen to transform $y_k$ into $y_{k+1}$? If this were true, that is a serious limitation. I breathed a sigh of relief when the authors clarified that they can reuse training samples, up to the push length. They discretized the push length by 5, and then got 1000 data points (image pairs) for each of those, for 5000 total. Then they find the optimum matrices (and actions, since matrices are actions here) by the ordinary least squares

Their deep models are referred to as DVF-Affine and DVF-Original. The affine one is designed for fairer comparison with the linear model, so it’s an image-to-image prediction model, with five separate neural networks for each of the discretized push lengths. DVF-Original takes the action as an additional input, while DVF-Affine does not.

Surprisingly, their results show that their linear model has lower prediction error on a held-out set of 1000 test images. This should directly translate to better performance on the actual task, since more accurate models mean the Lyapunov function will be driven down to 0 faster. Indeed, their results confirm the prediction error results, in the sense that linear models are the best or among the best in terms of task performance.

Now we get to the big question: why are linear models better than deeper ones for these experiments? I thought of these while reading the paper:

  • The carrots are very tiny in the images, so perhaps the 32x32 resolution makes it hard to accurately capture the fine-grained nature of the carrots.

  • The images are grayscale and small, which means linear models may work better as opposed to if the images were larger. At some point the “$N$” in their paper will grow too large to be used with linear models. (Of course with larger images, the problem of video prediction becomes exponentially harder. Heck, we only used 56x56 in our paper, and the SV2P paper used 64x64 images.)

  • Perhaps there’s just not enough data? It looks like the experiments use 23,000 data points to train DVF-Original, and 5,000 data points for DVF-Affine? For a point of comparison, we used about 105,000 images of cloth.

  • Furthermore, the neural networks are trained directly on the pixels in an end-to-end manner using the Frobenius norm loss (basically mean square error on pixels). In contrast, models such as SV2P are trained using Variational AutoEncoder style losses, which may be more powerful. In addition, the SV2P paper explicitly stated that they performed a multi-stage training procedure since a single end-to-end procedure tends to converge to less than ideal solutions.

  • Perhaps the problem has a linear nature to it? While reading the paper, I was reminded of the thought-provoking NeurIPS 2018 paper on how simple random search on linear models is competitive for reinforcement learning on MuJoCo environments.

  • Judging from Figure 11, the performance of the better neural network model seems almost as good as the linear one. Maybe the task is too easy?

Eventually, the authors discuss their explanation: they believe that their problem has natural linearity in it. In other words, there is inductive bias in the problem. Inductive bias in machine learning is a fancy way of saying that different machine learning models make different assumptions about the prediction problem.

Overall, the WAFR 2020 paper is effective and thought-provoking. It makes me wonder if we should have at least tried a linear model that could perhaps predict edges or corners of cloth while trying to abstract away other details. I doubt it would work for complex fabric manipulation tasks, but perhaps for simpler ones. Hopefully someone will explore this in the future!

Here are the papers discussed in this post, ordered by publication date. I focused mostly on the WAFR 2020 paper, and the others are: my paper with Ryan for RSS, the two main Visual Foresight papers, and the S2VP paper that uses the video prediction model we’ve used for our paper.