One reason why I enjoy working on robotics is because many of the problems the research community explores are variants of tasks that we humans do on a daily basis. For example, consider the problem of searching for and retrieving a target object in clutter. We do this all the time. We might have a drawer of kitchen appliances, and may want to pick out a specific pot for cooking food. Or, maybe we have a box filled with a variety of facial masks, and we want to pick the one to wear today when venturing outside (something perhaps quite common these days). In the robotics community, recent researchers that I collaborate with have formulated this as the mechanical search problem.

In this blog post, I discuss four recent research papers on mechanical search, split up into two parts. The first two focus on core mechanical search topics, and the latter two propose using something called learned occupancy distributions. Collectively, these papers have appeared at ICRA 2019 and IROS 2020 (twice), and one of these is an ICRA 2021 submission.

Mechanical Search and Visuomotor Mechanical Search

The ICRA 2019 paper formalizes mechanical search as the task of retrieving a specific target object from an environment containing a variety of objects within a time limit. They frame the general problem using the Markov Decision Process (MDP) framework, with the usual states, actions, transitions, rewards, and so on. They consider a specific instantiation of the mechanical search MDP as follows:

  • They consider heaps of 10-20 objects at the start.
  • The target object to extract is specified by a set of $k$ overhead RGB images.
  • The observations at each time step (which a policy would consume as input) are RGB-D, where the extra depth component can enable better segmentation.
  • The methods they use do not use any reward signal.
  • They enable three action primitives: (a) push, (b) suction, and (c) grasp.

The push action is there so that the robot can rearrange the scene for better suction and grasp actions, which are the primitives that actually enable the robot to retrieve the target object (or distractor objects, for that matter). While more complex action primitives might be useful for mechanical search, this would introduce complexities due to the curse of dimensionality.

Here’s the helpful overview figure from the paper (with the caption) showing their instantiation of mechanical search:


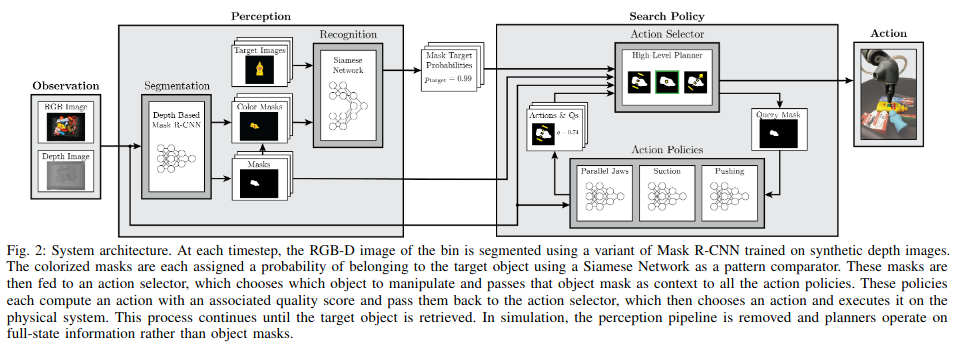
I like these type of figures, and they are standard for papers we write in Ken Goldberg’s lab.

The pipeline is split up into a perception stage and a search policy stage. The perception stage first computes a set of object masks from the input RGB-D observation. It then uses a trained Siamese Network to check the “similarity” between any of these masks, and those of the target images. (Remember, in their formulation, we assume $k$ separate images that specify the target, so we can feed all combinations of each target image with each of the computed masks.) If a target image is found, then they can run the search policy to select one of the three allowed action primitives, depending on the action primitive with the highest “score.” How is this value chosen? We can use off-the-shelf Dex-Net policies to compute the probability of action successes. Please refer to my earlier blog post here about Dex-Net.

Here are a couple of things that might not be clear upon a first read of the paper:

  • There’s a difference between how action qualities are computed in simulation versus real. In simulation, grasp and suction actions both use indexed grasps from a simulated Dex-Net 1.0 policy in simulation, which is easy to use as it avoids having to run segmentation. In addition, Dex-Net 1.0 literally contains a dataset of simulated objects plus successful grasps for each object, so we can cycle through those as needed.
  • In real, however, we don’t have easy access to this information. Fortunately, for grasp and suction actions, we have ready-made policies from Dex-Net 2.0 and Dex-Net 3.0, respectively. We could use them in simulation as well, it’s just not necessary.

To be clear, this is how to compute the action quality. But there’s a hierarchy: we need an action selector that can use the computed object masks (from the perception stage) to decide which object we want to grasp using the lower-level action primitives. This is where their 5 algorithmic policies come into play, which correspond to “Action Selector” in the figure above. They test with random search, prioritizing the target object (with and without pushing), and a largest first variant (again, with and without pushing).

The experiments show that, as expected, algorithmic policies that prioritize the target object and the larger objects (if the target is not visible) are better. However, a reader might argue that from looking closely at the figures in the paper, the difference in performance among the 4 algorithmic policies other than the random policy may be minor.

That being said, as a paper that introduces the mechanical search problem, they have a mandate to test the simplest types of policies possible. The conclusion correctly points out that an interesting avenue for future work is to do reinforcement learning. Did they do that?

Yes! This is good news for those of us who like to see research progress, and bad news for those who were trying to beat the authors to it. That’s the purpose of their follow-up IROS 2020 paper, Visuomotor Mechanical Search. It fills in the obvious gap made from the ICRA 2019 paper: that performance is limited by algorithmic policies, which are furthermore restricted to linear pushes parameterized by an initial point and then a push direction. Properly-trained learning-based policies that can perform continuous pushing strategies should be able to better generalize to complex configurations than algorithmic ones.

Since naively applying Deep RL is very sample inefficient, the paper proposes an approach combining three components:

  • Demonstrations. It’s well-known that demonstrations are helpful in mitigating exploration issues, a topic I have previously explored on this blog.
  • Asymmetric Information. This is a fancy way of saying that during training, the agent can use information that is not available at test time. This can be done when using simulators (as in my own work, for example) since the simulator includes detailed information such as ground-truth object positions which are not easily accessible from just looking at an image.
  • Mid-Level Representations. This means providing the policy (i.e., actor) not the raw RGB image, but something “mid-level.” Here, “mid-level” means the segmentation mask of the target object, plus camera extrinsics and intrinsics. These are what actually get passed as input to the mechanical search policy, and the logic for this is that the full RGB image would be needlessly complex. It is better to just isolate the target object. Note that the full depth image is passed as input — the mid-level representation just replaces the RGB component.

In the MDP formulation for visuomotor mechanical search, observations are RGBD images and the robot’s end-effector, actions are relative end-effector changes, and the reward is a shaped and hand-tuned to encourage the agent to make the target object visible. While I have some concerns about shaping rewards in general, it seems to have worked for them. While the actor policy takes in the full depth image, it simultaneously consumes the mid-level representation of the RGB observation. In simulation, one can derive the mid-level representation from ground-truth segmentation masks provided by PyBullet simulation. They did not test on physical robots, but they claim that it should be possible to use a trained segmentation model.

Now, what about the teachers? They define three hard-coded teachers that perform pushing actions, and merge the teachers as demonstrators into the “AC-Teach” framework. This is the authors’ prior paper that they presented at CoRL 2019. I read the paper in quite some detail, and to summarize, it’s a way of performing training that can combine multiple teachers together, each of which may be suboptimal or only cover part of the state space. The teachers use privileged information by not using images but rather using positions of all objects, both the target and the non-target(s).

Then, with all this, the actor $\pi_\theta(s)$ and critic $Q_\phi(s, a)$ are updated using standard DDPG-style losses. Here is Figure 2 from the visuomotor mechanical search paper, which summarizes the previous points:


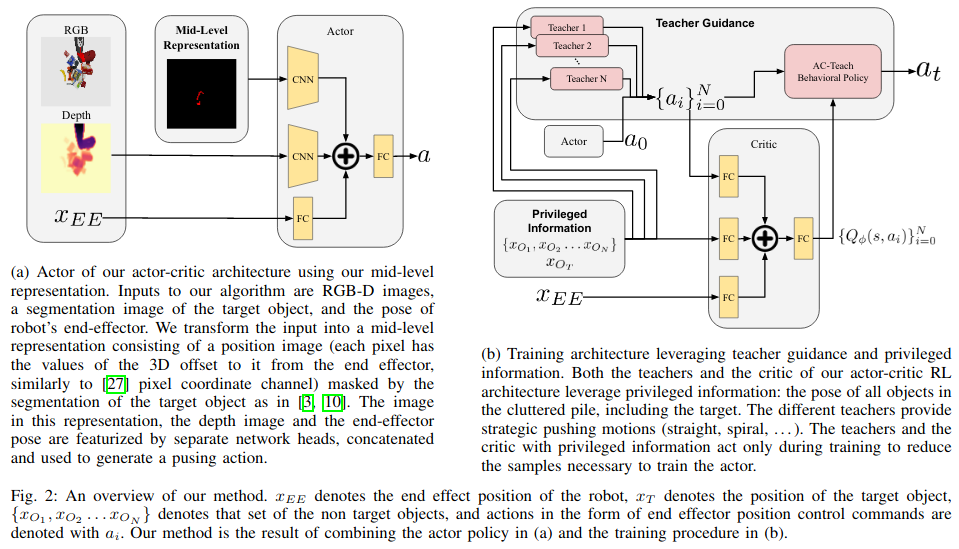
Remember that the policy executes these actions continuously, without retracting the arm after each discrete push, as done in the method from the ICRA 2019 paper.

They conduct all experiments in PyBullet simulation, and extensively test by ablating on various components. The experiments focus on either a single-heap or a dual-heap set of objects, which additionally tests if the policy can learn to ignore the “distractor” heap (i.e., the one without the target object in it) in the latter setting. The major future work plan is to address failure cases. I would also add that the authors could consider applying this on a physical robot.

These two papers give a nice overview of two flavors of mechanical search. The next two papers also relate to mechanical search, and utilize something known as learned occupancy distributions. Let’s dive in to see what that means.

X-RAY and LAX-RAY

In an IROS 2020 paper, Danielczuk and collaborators introduce the idea of X-RAY for mechanical search of occluded objects. To be clear: there was already occlusion present in the prior works, but this work explicitly considers it. X-RAY stands for maXimize Reduction in support Area of occupancY distribution. The key idea is to use X-RAY to estimate “occupancy distributions,” a fancy way of labeling each bounding box in an image with the likelihood that it contains the target object.

As with the prior works, there is an MDP formulation, but there are a few other important definitions:

  • The modal segmentation mask: regions of pixels in an image corresponding to a given target object which are visible.
  • The amodal segmentation mask: regions of pixels in an image corresponding to a given target image which are either visible or invisible. Thus, the amodal segmentation mask must contain the modal segmentation mask, as it has both the visible component, plus any invisible stuff (which is where the occlusion happens).
  • Finally, the occupancy distribution $\rho \in \mathcal{P}$: the unnormalized distribution describing the likelihood that a given pixel in the observation image contains some part of the target object’s amodal segmentation mask.

This enables them to utilize the following reward function to replace a sparse reward:

\[\tilde{R}(\mathbf{y}_k, \mathbf{y}_{k+1}) = |{\rm supp}(f_\rho(\mathbf{y}_{k}))| - |{\rm supp}(f_\rho(\mathbf{y}_{k+1}))|\]

where \(f_\rho\) is a function that takes in an observation \(\mathbf{y}_{k}\) (following the paper’s notation) and produces the occupancy distribution \(\rho_k\) for a given bounding box, and where \(|{\rm supp}(\rho)|\) for a given support \(\rho\) (dropping the $k$ subscript for now) is the number of nonzero pixels in \(\rho\).

Why is this logical? By reducing the occupancy distribution, one decreases the number pixels that MIGHT occlude the target objects, hence reducing uncertainty. Said another way, increasing this reward gives us greater certainty as to where the target object is located, which is an obvious prerequisite for mechanical search.

The paper then describes (a) how to estimate $f_\rho$ in a data-driven manner, and then (b) how to use this learned $f_\rho$, along with $\tilde{R}$, to define a greedy policy.

There’s an elaborate pipeline for generating the training data. Originally I was confused about their procedure for translating the target object. But after reading carefully and watching the supplementary video, I understand; it involves simulating a translation and rotation while keeping objects fixed. Basically, they pretend they can repeatedly insert the target object at specific locations underneath a pile of distractor objects, and if it results in the same occupancy distribution, then they can include such images in the data to expand the occupancy distribution to its maximum possible area (by aggregating all the amodal maps), meaning that estimates of the occupancy distribution are a lower bound on the area.

As expected, they train using a Fully Convolutional Network (FCN) with a pixel-wise MSE loss. You can think of this loss as taking the target image and the image produced from the FCN, unrolling them into long vectors \(\mathbf{x}_{\rm targ}\) and \(\mathbf{x}_{\rm pred}\), then computing

\[\|\mathbf{x}_{\rm targ} - \mathbf{x}_{\rm pred}\|_2^2\]

to find the loss. This glosses over a tiny detail: the network actually predicts occupancy distributions for different aspect ratios (one per channel in the output image) and only the channel with the similar input aspect ratio gets considered for the loss. Not a huge deal to know if you’re skimming the paper: it probably suffices to just realize that it’s the standard MSE.

Here is the paper’s key overview figure:


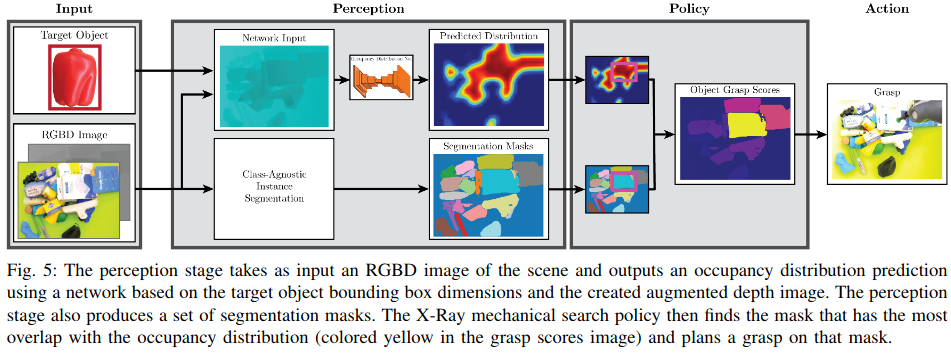
They propose to plan a grasp with the most amount of corresponding occupancy area. Why? A pick and place at that spot will greatly reduce the subsequent occupancy area of the target object.

It is nice that these FCNs can reasonably predict occupancy distributions for target objects unseen in training, and that it can generalize to the physical world without actually training on physical images. Training on real images would be harder since depth images would likely be noisier.

The two future works they propose are: relieving themselves of the assumption that the target object is flat, and (again) saying that they will do reinforcement learning. This paper was concurrent with the visuomotor mechanical search, but that paper did not technically employ X-RAY, so I suppose there is room to merge the two.

Next, what about the follow-up work of LAX-RAY? This addresses an obvious extension in that instead of top-down grasping, one can do lateral grasping, where the robot arm moves horizontally instead of vertically. This enables application to shelves. Here’s the figure summarizing the idea:


We can see that a Fetch robot has to reveal something deep into the shelf by pushing objects in front to either the left or the right. The robot has a long thin board attached to its gripper, it’s not the usual Fetch gripper. The task ends as soon as the target object, known beforehand, is revealed.

As with standard X-RAY, the method involves using a Fully Convolutional Network (FCN) to map from an image of the shelf to a distribution of where the target object could be. (Note: the first version of the arXiv paper says “fully connected” but I confirmed with the authors that it is indeed an FCN, which is a different term.) This produces a 2D image. Unlike X-RAY, LAX-RAY maps this 2D occupancy distribution to a 1D occupancy distribution. The paper visualizes these 1D occupancy distributions by overlaying them on depth images. The math is fairly straightforward on how to get a 1D distribution: just consider every “vertical bar” in the image as one point in the distribution, then sum over the values from the 2D occupancy distribution. That’s how I visualize it.

The paper proposes three policies for lateral-access mechanical search:

  • Distribution Area Reduction (DAR): ranks actions based on overlap between the object mask and the predicted occupancy distribution, and picks the action that reduces the sum the most. This policy is the most similar, in theory, to the X-RAY policy: essentially we’re trying to “remove” the occupancy distribution to reduce areas where the object might be occluded.
  • Distribution Entropy Reduction over n Steps (DER-n): this tries to predict what the 1D occupancy distribution will look like over $n$ steps, and then picks the one with lowest entropy. Why does this make sense? Because lower entropy means the distribution is less spread out, and concentrated towards one area, telling us where the occluded item is located. The authors also introduce this so that they can test with multi-step planning.
  • Uniform: this tests a DAR ablation by removing the predicted occupancy distribution.

They also introduce a First-Order Shelf Simulator (FOSS), a simulator they use for fast prototyping, before experimenting with the physical Fetch robot.

What are some of my thoughts on how they can build upon this work? Here are a few:

  • They can focus on grasping the object. Right now the objective is only to reveal the object, but there’s no actual robot grasp execution. Suctioning in a lateral direction might require more sensitive controls to avoid pushing the object too much, as compared to top-down where gravity stops the target object from moving away.
  • The setup might be a bit constrained in that it assumes stuff can be pushed around. For example consider a vase with water and flowers. Those might be hard to push, and are at risk of toppling.

Parting Thoughts

To summarize, here is how I view these four papers grouped together:

  • Paper 1: introduces and formalizes mechanical search, and presents a study of 5 algorithmic (i.e., not learned) policies.
  • Paper 2: extends mechanical search to use AC-Teach for training a learned policy that can execute actions continually.
  • Paper 3: combines mechanical search with “occupancy distributions,” with the intuition being that we want the robot to check the most likely places where an occluded object could be located.
  • Paper 4: extends the prior paper to handle lateral access scenarios, as in shelves.

What are some other thoughts and takeaways I have?

  • It would be exciting to see this capability mounted onto a mobile robot, like the HSR that we used for our bed-making paper. (We also used a Fetch, and I know the LAX-RAY paper uses a Fetch, but the Fetch’s base stayed put during LAX-RAY experiments.) Obviously, this would not be novel from a research perspective, so something new would have to be added, such as adjustments to the method to handle imprecision due to mobility.
  • It would be nice to see if we can make these apply for deformable bags, i.e., replace the bins with bags, and see what happens. I showed that we can at least simulate bagging items in PyBullet in some concurrent work.
  • There’s also a fifth mechanical search paper, on hierarchical mechanical search, also under review for ICRA 2021. I only had time to skim it briefly and did not realize it existed until after I had drafted the majority of this blog post. I have added it in the reference list below.

References