I spent roughly a year preparing, and then interviewing, for tenure-track faculty positions. My job search is finally done, and I am joining the University of Southern California as an Assistant Professor in the Computer Science department, starting in August 2023. I am now scrambling to get started, to find housing, etc.

In case you are interested, I have documented my faculty application story here in this Google Doc.

I sincerely thank everyone who helped me get to where I am today.

At the end of every year I have a tradition where I write summaries of the books that I read throughout the year. Unfortunately this year was exceptionally busy (the postdoc life is a lot more intense than the PhD life) so I didn’t write summaries. I apologize in adevance.

You can find the other book-related blog posts from prior years (going back to 2016) in the blog archives.

Here are the 17 books I read this past year. I put in parentheses the publication date.

The books which I really enjoyed are written in bold.

• Impact Players: How to Take the Lead, Play Bigger, and Multiply Your Impact (2021)
• Never Split the Difference: Negotiating As If Your Life Depended On It (2016)
• Be Exceptional: Master the Five Traits That Set Extraordinary People Apart (2021)
• The Digital Silk Road: China’s Quest to Wire the World and Win the Future (2021)
  • A lot of China’s recent development happened by importing Western technology, and the book clarifies that much of this was due to technology sharing agreements that were legal (and to which Western companies agreed). The book explores the corresponding consequences. While it’s clear that the author (like myself) is not the most politically aligned to the Chinese Communist Party (to put it mildly), the best part of the book is near the end when it says: But there is a line between anxiety and paranoia, and crossing it carries dangers all its own. During World War II, FDR made the horrific decision to force 120,000 people of Japanese ancestry into internment camps. […] The United States must guard against xenophobia and racism as well as protectionism. From what I understand, my Japanese-American grandfather (and his parents) were, fortunately, never sent to these camps. But their family business of selling Japanese pastries suffered substanially during World War II.
• Infidel: My Life (2007)
• Metabolical: The Lure and the Lies of Processed Food, Nutrition, and Modern Medicine (2021)
• Antisocial: Online Extremists, Techno-Utopians, and the Hijacking of the American Conversation (2019)
• Culture Warriors: My Journey Into the Dark Web of White Supremacy (2020)
• Inevitable: Understanding the 12 Technological Forces That Will Reshape our Future (2016)
• Your Data, Their Billions: Unraveling and Simplifying Big Tech (2022)
• The End of History and the Last Man (1992)
  • About time!
• Winter is Coming: Why Vladimir Putin and the Enemies of the Free World Must Be Stopped (2015)
  • It should be clear why I read this book. As Garry Kasparov frequently says these days, “Stop telling me I was right and listen to what I’m saying now.”
• Ukraine: What Everyone Needs to Know (2020)
• Coalitions of the Weak: Elite Politics in China from Mao’s Stratagem to the Rise of Xi (2022)
  • These days, one of my hobbies is studying Chinese politics, and this book is a perfect example of me engaging in that. I find the subject fascinating.
• Spin Dictators: The Changing Face of Tyranny in the 21st Century (2022)
  • Co-written by Sergei Guriev (Professor of Economics at Sciences Po, Paris) and Daniel Treisman (Professor at UCLA). The book takes a critical look at various governments and leaders, and uses the term “spin dictators” for rulers who try and cloak their techniques under the name of democracy. One of these authors had to flee his home country for his safety (prior to working on this book). You can probably guess who. I’m forever grateful that I (hopefully) will never need to do this.
• Reprogramming the American Dream: From Rural America to Silicon Valley―Making AI Serve Us All (2020)
• The Vortex: A True Story of History’s Deadliest Storm, an Unspeakable War, and Liberation (2022).
  • I knew next to nothing about Bangladesh before reading this book and I’m amazed at all the history packed into this book. I also commend the authors for clarifying how they derived their sources and conducted their research. This should be standard.

The airplanes on display at the CoRL 2022 banquet.

At the end of my last post which belatedly summarized RSS 2022, I mentioned I was also attending CoRL 2022 in a much farther away city: Auckland, New Zealand. That conference has now concluded and I thought it went well. I attended CoRL for a few reasons.

• I was presenting our recent ToolFlowNet paper, which is one of the major projects that I have worked on during my postdoc.
• I was part of the inclusion committee at CoRL, so I also got partial funding to attend.
• The conference is well aligned for my research interests.
• New Zealand is really nice at this time of the year.

Unlike most of my prior conference reports where I write them as blog posts, here I have notes in this Google Doc. I was working on this while at CoRL, and it would take a lot of time to convert these to something that looks nice on the website, and Google Docs might be easier for me to do quick edits if needed.

If robot learning is of interest to you, I hope you enjoy these conference notes. See you next year in Atlanta, Georgia, for CoRL 2023.

A photo I took while at RSS 2022 in New York City, on the dinner cruise arranged by the conference.

From June 27 to July 01 this year, I attended the latest the Robotics: Science and Systems conference. This was the first in-person RSS after two virtual editions in 2020 and 2021. I don’t publish in RSS frequently. I only have one RSS paper, VisuoSpatial Foresight, from 2020. I was attending mainly because of its nearby location in New York City and because I was invited to attend RSS Pioneers, which is a unique event arranged by this conference.

I’m well aware that this report, like the one I wrote for ICRA 2022, is coming well after the conference has ended. Things have been extremely busy on my end but I will try and improve the turnaround time between attending and reporting about a conference.

RSS 2022: Pioneers

For the first day, I arrived on campus for RSS Pioneers, which happened the day before the “official” RSS conference. To quote from the website:

RSS Pioneers is an intensive workshop for senior Ph.D. students and early career researchers in the robotics community. Held in conjunction with the main Robotics: Science and Systems (RSS) conference, each year the RSS Pioneers brings together a cohort of the world’s top early-career researchers. The workshop aims to provide these promising researchers with networking opportunities and help to navigate their next career stages, and foster creativity and collaboration surrounding challenges in all areas of robotics. The workshop will include a mix of research and career talks from senior scholars in the field from both academia and industry, research presentations from attendees and networking activities.

I arrived early as usual to meet the sign language interpreters, which I had requested well in advance. (Columbia University paid the bill since they were hosting the conference.) We had some minor hiccups at the start when the security guards wouldn’t let the interpreters inside with me. Columbia Mechanical Engineering professor Matei Ciocarlie was the local arrangements chair of RSS and thus in charge of much of the day-to-day affairs, and he kept trying to explain to the security guards why there were there and why we all had to be allowed inside. Eventually he convinced the security guards, and I arrived just in the nick of time.

During RSS Pioneers, the 30 or so “Pioneers” gave brief presentations of our research. I presented my recent theme of robot learning for deformable manipulation. There were also talks from professors, which for Pioneers was an interesting mix of both technical talks and high-level thoughts. Some of the “high-level” aspects of the talks included de-emphasizing rankings of the school, the different research cultures of the United States and Europe, how (not) to compare one’s research with others, and dealing with publish-or-perish. Throughout the day, we had brief social breaks, and ultimately, the real value of this event is probably that we get to know other Pioneers and increase our connections with the robotics field. Personally, it took me a while to view myself as a roboticist. Overall I’m happy I attended this year’s edition.

RSS 2022: The Conference

The actual conference and “conference workshops” (hereafter, just “workshops”) started the next day, with the first and fifth days for workshops. An interesting workshop I attended was about “Overlooked Aspects on Imitation Learning.” In general, as per my rule for attending these events, I tried not to get bogged down by attending every talk in a workshop, and instead I spent some time in a common room area where they had food and snacks, to see if other attendees were available for impromptu chats.

In between the two workshop days, the conference had the usual set of keynotes and paper presentations. A lot of the interesting papers to me were ones that I already knew of in advance (thanks to arXiv, Twitter, and the like) such as DextAIRity, Iterative Residual Policy, and Autonomously Untangling Long Cables, all three of which garnered awards (or were finalists for them). An interesting paper which I did not know about in advance was You Only Demonstrate Once. From a technical perspective, I think it’s a very nice systems paper which combines a variety of techniques: using specialized objects coordinate spaces (called “NUNOCS” in the paper), a motion tracker, category-level behavioral cloning, etc. I should also give a shout-out to the FlowBot3D paper from our lab, which was one of the best paper finalists. I am not an author, but my ToolFlowNet paper for the upcoming Conference on Robot Learning (CoRL) builds upon FlowBot3D with similar ideas.

A unfortunate thing is that, as with ICRA earlier this year, we continually ran into technical problems with speakers unable to reliably connect their laptops to the projectors. In one particularly unfortunate oral presentation, the projector strangely turned off, then on, at regular intervals. I counted an interval time of about 10 seconds where, without fail, the projector would turn off and on, almost perfectly on cue! I felt very sorry for the speaker. Is there any way that we can improve the state of affairs for connecting to projectors? It seems to be a universal problem.

In addition to talks, poster sessions, and coffee break chats, since RSS was at Columbia University. I was fortunate to get a semi-private tour of the Columbia robotics lab. I saw FlingBot and DextAIRity in action. I thank the members of Shuran Song’s lab who gave me this tour. Having a set of coordinating UR5 arms in one setup has been great for their research acceleration.

RSS does not provide lunch or dinner for each day, but as is typical in academic conferences in my circle, one of the nights is dedicated to a “fancy” dinner event. For this year’s edition, RSS had dinner on a cruise ship which took us around lower Manhattan. The food was incredibly delicious and diverse, and perhaps the best I have eaten at a conference – there were salads, vegetarian dishes, fish, chicken, fancy desserts, and a bunch of stuff I can’t recall. Obviously this service doesn’t come cheap. I heard it’s about 150 USD per person. Aided by the interpreter who did a tremendous job in the noisy context, I had a bunch of intellectually stimulating conversations which I recall included robotics (obviously), politics (should the US military fund robotics research), and my future job plans (one can only be a postdoc for so long).

The conference also had a town hall, to solicit feedback from us. This is a good thing, and I appreciate RSS for doing this. Some of the questions had to do with the nature of what a “systems” paper means. Other questions had to do with reducing stress on students and researchers. One of the paper awards for RSS is a “Best systems paper award in honor of Seth Teller.” Seth Teller was a professor at MIT and passed away in 2014 from suicide.

From the closing ceremonies, we learned that RSS 2023 will be in Daegu, South Korea next year, which is the first time it’s being held in Asia. This is a good thing for the sake of balance, given the recent US-heavy tilt on conferences. It will pose some issues for me if I were to request sign language interpreters, but I am OK with balancing the location of conferences since we need to consider the full community’s needs (not just mine) when picking locations.

RSS 2022: Overall Impressions

I was fortunate to attend RSS in person for the first time in my career. The conference is much smaller compared to ICRA and IROS and is single-track, which meant I did not feel overwhelmed with competing priorities. I exceeded my expectations in meeting people and understanding the work they do. Certainly, being part of RSS Pioneers helped, and I would recommend this to senior PhD students and postdocs.

Columbia University’s in a fantastic location in New York City which makes travel to and from it easier. The subway system made transportation within the city easier, and there’s a lot of food nearby with a range of prices, not to mention attractions and museums. (Alas, I wish I had the time to spend a few extra days in NYC to explore it more…) The location also meant that, as is typically the case in big American cities, securing sign language interpreters generally isn’t too difficult. Of course, there are some inevitable challenges with space that come with NYC, and we might have seen that with the poster sessions at RSS, since they were in narrow ramps and stairs in one building. In contrast, ICRA 2022 in Philadelphia was not at the University of Pennsylvania campus but at the Pennsylvania Convention Center with massive space.

RSS has some differences in terms of paper structure and reviewing as compared to ICRA and IROS. At RSS, there’s a longer page limit requirement, and since page limits in practice serve as lower bounds (since no one wants to be viewed as lacking content) that means papers have more material. At RSS there’s a slightly stricter acceptance rate and a more involved reviewing process (often with rebuttals) compared to other conferences. However, I’m well aware that this is subject to enormous variance in paper quality. But my point is: RSS papers tend to be high quality so if I see that a paper was presented there, it already hits some minimum quality threshold for me.

In terms of the content, RSS is becoming increasingly similar to the [Conference on Robot Learning (CoRL)]. A lot of RSS papers use machine learning. Matei Ciocarlie, the local arrangements chair, seems to have a similar interpretation and said to me: “oh, they [the RSS workshops] were all in robot learning …” A lot of RSS and CoRL papers could be interchangeable, in that papers accepted to RSS, assuming they have some robot learning aspect, could be accepted at CoRL and possibly vice versa. I have frequently seen cases when researchers submit papers to RSS, get rejected, improve the paper (to varying extents…), and get the paper accepted to CoRL. The reverse isn’t generally true since CoRL rejections tend to go to the following ICRA due to the timing.

Given its full name as Robotics: Science and Systems, this might mean RSS papers have more of a physical robotics “system” aspect as compared to CoRL, though I am not sure if this applies in practice. UIUC Professor Kris Hauser chaired this edition’s conference and he wrote this Medium article on what it means to write a systems-related robotics paper. Whether the community follows through on this is another matter, and there were some questions about the “systems” aspect research in the RSS town hall.

In sum, to those who helped organize this year’s RSS conference, thank you very much!! I feel very fortunate to have attended and I hope to do so again in future editions.

Finally, regarding CoRL, that conference is happening in a few days in Auckland, New Zealand. If you are attending, I will also be there and am happy to chat …

A photo I took while at ICRA 2022 in Philadelphia. This is the "Grand Hall" area where we had the conference reception. There are a lot of (more professional) photos on the conference website.

At long last, after more than two years of virtual conferences, last May I attended an in-person conference, the 2022 International Conference on Robotics and Automation (ICRA), from May 23-27. The last in-person conferences I attended were ISRR 2019 in Hanoi, Vietnam and NeurIPS 2019 in Vancouver, Canada (blog posts are here and here). Apologies for the massive months-long delay in blogging. One challenge with ICRA’s timing is that it was few weeks before the CoRL 2022 deadline, and so I (and many other attendees, as I would soon learn) were busy trying to work on our paper submissions.

Background and Context

ICRA is a large conference, held annually since 1984. You can find the list of past and future venues here. The last full in-person ICRA was in 2019 in Montreal, Canada. This year, it was in Philadelphia in a former train station converted to a large conference convention center. Philadelphia (or “Philly” as it’s often referred to in informal parlance) is also important in the political development of the United States and near the convention center are relevant museums and historical landmarks such as the Liberty Bell.

As with many other 5-day academic conferences and consistent with prior ICRAs, two are for workshops and three are for the main conference. Fortunately, I was able to attend the entire thing, plus stay an extra day after ICRA to explore Philly; call it a one-day vacation if you like.

I went to ICRA for several reasons. First, I wanted to return to an in-person conference experience. Second, it’s close: I work at CMU now, which is in the same state of Pennsylvania (albeit on the opposite side) so the travel isn’t too bad. Third, for the first time in my research career, I was a co-organizer of a workshop. Fourth, I also had a paper accepted which we called Planar Robot Casting, led by outstanding undergraduate researcher Vincent Lim and PhD student Huang (Raven) Huang. Yes, in case you’re wondering, we deliberately chose the PRC acronym because it matches the People’s Republic of China.

Another positive aspect of ICRA for me in particular is that ICRA and other IEEE conferences now have a new policy that explicitly allocates funding for compliance with the Americans for Disabilities Act (ADA). In 2020, my PhD advisors and I began asking the IEEE Robotics and Automation Society (RAS) to encourage them to provide funding for academic accommodations for all RAS-sponsored conference. Here’s a mid-2021 tweet by my PhD advisor Ken Goldberg summarizing what happened. Though he mentions me in his tweet, the real credit here goes to him and Torsten Kröger, and I thank both of them for their support. In the past, I would arrange for such academic accommodations to the conference by asking my university, but having the conference pay is probably the more appropriate outcome. Furthermore, while the impetus of this was my specific accommodation need, I hope this will extend for other accommodations.

I emailed ICRA a few months before the conference to get them to arrange for sign language interpreters. Rule of thumb: the process always takes longer than expected, so start early! After a long list of back-and-forth emails, ICRA was able to arrange for the services and it turned out quite well. Certainly, having the conference located in the United States was another plus. We’ll see if the process works out similarly well for ICRA 2023 in London, UK or ICRA 2024 in Yokohama, Japan. Hopefully the same staff members will be involved, as that might simplify the process considerably.

My Experience

On the first day, I arrived early to the convention center. The first reason was to meet the sign language interpreters, who often arrive early for such events. For me, it’s critical to also get there early so I can introduce myself to them.

The other reason for my early arrival was that I was one of the three lead co-organizers for the 2nd Workshop on Deformable Object Manipulation, along with Martina Lippi and Michael Welle. Those two were among the lead organizers last year and kindly invited me to help co-organize this year’s edition. Michael and I handled the in-person logistics for the workshop while Martina (in Italy) did a tremendous job holding the fort for all the remote needs.

We had a bit of a tight start to the workshop, because for some reason, either our room or our workshop was not properly registered with the conference and thus we didn’t have a microphone, a video projector, and other ingredients. Michael was able to hastily arrange for the conference staff to get the materials in time, but it was close. We also had issues with the microphone and audio in the morning and had to ask the convention staff to check. Other than the initial hiccups, I though the workshop went well. We had high attendance, especially for a workshop that was on the far end of the conference center. I’m guessing we regularly had 100 people in the room throughout the day (the exact number varied since people came in and out all the time). I met a lot of the authors and attendees, and I hope they all enjoyed the workshop as much as I enjoyed co-hosting and co-organizing it.

It was a nice experience, and I would be happy to organize a workshop again in the near future. I would write another blog post on “lessons learned” but this is still just my first time organizing so I don’t want to make any non-generalizable claims, and Rowan McAllister has already written a nice guide.

Later, we had the conference welcome reception in a larger space, where we could stand and grab food and drinks from various stalls. As usual, some of the food was distinctively local. We had Philadelphia-themed cheesesteaks which I tried and thought were good. These aren’t things I would normally eat, but it’s good to experience this once in my life. In fact I didn’t even realize Philly was known for cheesesteaks before coming to ICRA.

Then we had the next three conference days. I spent the mornings attending the major talks, and then the rest of the days doing my best to talk with as many people and groups as possible. Fortunately, it was much easier than I expected to snag impromptu conversations. I made a few “semi-formal” plans by emailing people to ask for meeting times, but for the most part, my interactions were highly random. I’m not sure if that’s the case for most people who attended the conference?

I tried to set my time so that my first priority was to talk with people. Then, my next priority was to explore the posters and company exhibits. If there was nothing else to do, then I would attend the smaller talks from authors of research papers. There were a few other events at ICRA that I recognized from prior years such as robots racing through small tracks. I don’t get too involved in such competitions as I worry they could detract from my research time.

Regarding communication and masks, there was a mix of people wearing their own masks and those eschewing masks. Most who wore masks were wearing N95 or other relatively high-quality masks. My communication with others at the conference definitely benefited enormously by having sign language interpreters, without which I would be constantly asking people to take off their masks when talking to me (I don’t like doing this).

The fifth and last day of the conference consisted of another day of workshops. It’s also one that I wasn’t able to experience too much. I spent most of the day working on my CoRL 2022 submission. I did this at the conference hotel due to the poor WiFi at the conference, but the hotel was very close by and could be accessible without walking outside. I also would later learn that other conference attendees were doing something similar as me. While “robot learning” is a subset of “robotics”, the CoRL community is growing in size (the 2022 edition had a record 505 submissions) and is an increasingly larger fraction of the overall ICRA community.

After the conference, I spent another full day in Philadelphia briefly exploring the nearby historical and political museums and landmarks. For example, I took a brief visit to the National Constitution Center.

A photo I took while inside the National Constitution Center after ICRA.

But, as mentioned earlier, I did not have too much spare time at my disposal. Thus, after briefly touring some of the city, I ordered a salad from Sweetgreen for dinner (at least they have them in Philly, unlike in Pittsburgh!), and to drink, I bought some low-sugar Boba from a small store in the Chinatown next to the convention center. Then, it was back to my hotel room to work on a paper submission. Since my flight was scheduled to leave very early the next morning, I opted to skip sleeping and just worked straight until around 3:30AM. Then I got an Uber ride to the airport and flew back to Pittsburgh.

Overall Impressions

Overall, I had a nice experience at ICRA 2022. When I look back at all the academic conferences that I have attended in my career, I clearly had the best networking experience I ever had at a conference. This was the first conference where I aimed from the beginning to spend less time attending talks and more time talking with people in smaller conversations. I also met a lot of people who I only knew from online interactions beforehand. I kept a document with a list of all these new interactions, and by the end of ICRA, I had met over 50 new people for the first time.

As always, there are some positives and negatives about the conference. In terms of the things that could be interpreted as negatives, a few come to mind:

• For our workshop, we had some technical problems, such as our room being the only workshop room not initially assigned a video projector system as mentioned earlier. We also had the inevitable audio and microphone issues, and multiple attendees told us that they couldn’t hear speakers well. Also as expected, the hybrid format with online versus in-person attendees posed issues in that online speakers could often not hear speakers in the physical room. To clarify, besides the fact that our workshop and/or room didn’t seem to be properly registered at first, all these issues have been common in other conferences. I just wish there was a really easy way to get all the audio systems set up nicely. It seems like AV control systems are a universal headache.

• There are strict union rules in Philadelphia which led to some surprises. For example, the conference convention employees arranged a set of poster boards for workshops, but if we moved those poster boards (e.g., across the hallway to be closer to a workshop room) which we did for our workshop since it was on the far end of a hallway, then the union could fine ICRA.

• There seemed to be universal agreement among attendees that the food quality was not ideal. In my view, ICRA 2018 and 2019 had slightly better conference food offerings. This might be a downstream effect of COVID. Fortunately, there were a lot of food options in Philly near the convention center.

• The WiFi was highly unreliable. This was problematic for us who were working on CoRL submissions. In fact, one conference attendee told me he was resorting to hand-writing (on his iPad) parts of his CoRL submission while at the conference (and then he would type it up in Overleaf in the hotel which had better WiFi). I did something similar by skipping most of the 5th day of ICRA to stay in my hotel to work on CoRL. Admittedly, the timing of CoRL was unfortunate, and this is not ICRA’s fault.

• COVID isn’t actually over, and there are likely new variants circulating. I don’t know how many of the conference attendees tested positive afterwards. Whatever the case, I think it remains imperative for us to watch for the health of the community and to try and arrange for conference venues that will maximize the amount of physical space available. I know this is not easy for a conference like ICRA. During some of the dinners and receptions, many people were packed in tight quarters. In-person conferences will continue so I hope the community will develop best practices for mitigating infections. Despite the many technical challenges with combining in-person and virtual experiences, I think conferences should continue offering virtual options and not require paper authors to attend.

And yet … when I look at what I wrote above, I almost feel like these are nitpicks. Putting together a massive conference with thousands of people is incredibly complex with hundreds of administrative tasks that have to be done, and getting something that works for everyone is impossible. I sincerely appreciate and respect all the hard work that has to be done to execute a conference of this magnitude. In the end, maybe we should just focus on how fortunate we are that we can get together for a conference? Look at all the excitement in the photos from the conference here. Academic life is attractive for a reason, and so many of us (myself included for sure) are so fortunate that we can be a part of this exciting field. I can’t wait to see how robotics evolves going forward, and I hope many others share this excitement.

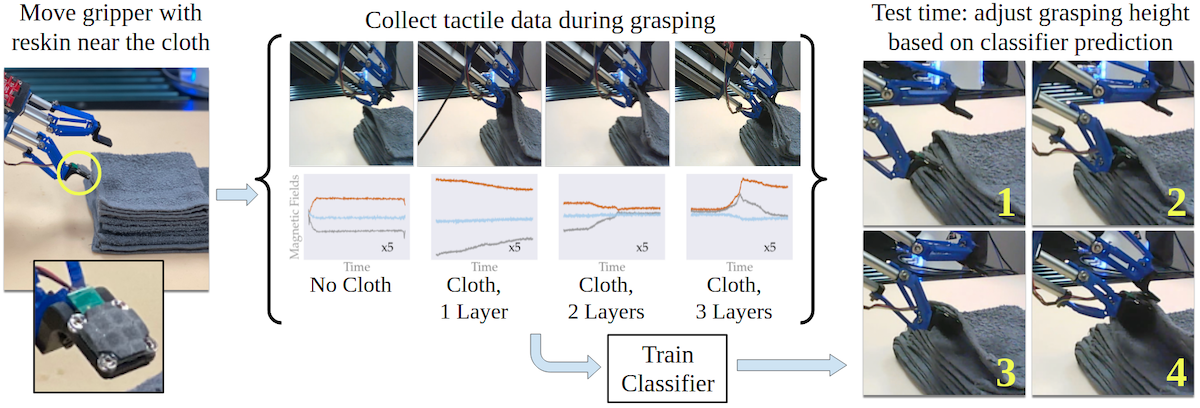
The system for our IROS 2022 paper on singulating layers of cloth with tactile sensing.

In collaboration with my colleagues at Berkeley and CMU, we recently uploaded two papers to arXiv on robotic fabric manipulation:

• Efficiently Learning Single-Arm Fling Motions to Smooth Garments, for ISRR 2022.
• Learning to Singulate Layers of Cloth using Tactile Feedback, for IROS 2022.

Robotic fabric (or cloth) manipulation is a recurring theme in my research, and these two papers continue the trend. The first paper, which we started a while back in Spring 2021, is about dynamic fabric manipulation; it can be thought of as an extension of our earlier ICRA papers on “Robots of the Lost Arc” and “Planar Robot Casting” while incorporating ideas from Huy Ha and Shuran Song’s legendary FlingBot paper. While FlingBot uses two arms, many robots have only one arm, and we show how to parameterize the action space in a way to make the search space tractable for learning. It was really fun to work with this “DMODO” team (Dynamic Manipulation of Deformable Objects) over the last few years and I hope to continue doing so.

I am also very excited about the second paper. This is my first paper developed entirely at CMU, and it’s also my first one which incorporates tactile sensing. When I first pitched project ideas to my postdoc host while he was interviewing me last year, I suggested using tactile sensing for fabric manipulation to give a robot local information that it might not get from vision (e.g., due to occlusions), and as such I’m really happy that we got this system working.

Specifically, we focus on multi-layer fabric manipulation, which occurs all the time when trying to fold and unfold fabrics such as clothing. Grasping an incorrect number of fabric layers has been a recurring failure in our prior work on fabric smoothing and folding. As is typical for me, many of my research ideas arise out of thinking about how I can address existing failure cases. After initially trying the GelSight sensor (used by many at CMU), we ended up using the ReSkin sensor (a CMU research product … anyone seeing a trend?) which has a small form factor to allow the robot to singulate and separate layers. While the actual machine learning in this paper is a little less relative to my other papers, I’m OK with this if it’s the approach that worked the best out of what we tried. In my view there’s no need to force more complex and elegant algorithms for the sake of doing so if those are not the right tool for the problem.

Incidentally, neither of these two papers use a fabric simulator. I invested an enormous amount of time trying to get one working for the tactile sensing paper, but it didn’t work out. I’m really thankful, therefore, that my wonderful colleagues Sashank Tirumala and Thomas Weng resolved a lot of the hardware details in time for the paper.

These papers have been accepted to ISRR 2022 and IROS 2022 for presentation later this year. The conferences are at really interesting locations: Geneva, Switzerland for ISRR and Kyoto, Japan for IROS. Given its location, and the offensive, unprovoked wars going on in parts of the world, I hope ISRR will include some information about the Geneva Conventions as part of the conference experience. If you’re curious, the last ISRR was in 2019 just before COVID in Hanoi, Vietnam. I attended that conference to present a paper and blogged about it daily, a habit which I am less likely do these days due to limited bandwidth. (The main “social” aspect of ISRR 2019 was a tour of Halong Bay.)

I hope those who are going to the conferences have the chance to discuss these papers with my colleagues. For various reasons, I am not planning to attend either conference in person. At least the papers themselves are now on arXiv and fit for research consumption. Let us know if you have any questions.

Scott Aaronson is a professor of computer science at UT Austin, where his research area is in theoretical computer science. However, he may be more well known in the broader computer science community for his popular blog Shtetl Optimized, which he began in 2005 and still updates regularly.

I found his blog back in the early 2010s when I started my journey into computer science, and I was hooked by his writing style. His blog also has a large readership, and most of his posts garner a fair amount of comments. What surprises me is that, as a busy professor like him, he still takes the time to talk to random commenters – such as myself on many occasions – to answer questions on almost any topic. There’s even a Scientific American blog post titled “Scott Aaronson Answers Every Ridiculously Big Question I Throw at Him”. My one contribution to his actual research career was providing him with some LaTeX code that he could copy and paste into a document to get a diagram to show. I hope I was able to save him some time.

Lately, his blog has attracted some vicious trolls who are attacking him and his family. It’s gotten bad enough that he’s now considering changing his commenting policy. It pains me to see people perform these actions, and I completely condemn such actions.

As a disclosure, it’s true that I often agree with him on many issues. For example, both Scott and I are strong supporters of our international colleagues, and one of my favorite posts from Scott was this one from 2017 when he defended Iranian students from America’s “travel ban.” He, like myself, seems to be careful to make the distinction between the government of Iran and students from Iran. His post was one of the reasons why I decided to write this somewhat related post a few months ago. Scott also gathered some notoriety back in 2014 when he described growing up shy and feeling isolated. When I was reading his posts, I often thought of myself since I, too, felt socially isolated growing up, though the main underlying cause (due to my hearing impairment) is different.

On the other hand, I have never met Scott personally, and from reading his blog, I can identify issues of disagreement. In fact, if I couldn’t find any areas of disagreement, I would be concerned about myself! So, I don’t want to be someone who will always defend him 100% no matter what. I just want to defend him against these specific trolls who are attacking him and his family.

I also think it is important to be consistent in my application of this belief, so if other researchers are experiencing their own ad-hominem attacks, the onus would be on me to defend those researchers as well. Please let me know if I am inconsistent in my application of this belief.

Boaz Barak, a professor at Harvard and a friend of Scott Aaronson, has a nice blog post here. I was touched by reading this and I couldn’t have said it better myself.

I hope I never become that kind of person who flings vicious attacks and insults to people and their families. I also hope I will one day have the honor of meeting Scott Aaronson in person.

This is a regularly updated post, last updated November 16, 2024.

In academia, for better or worse, we have what’s called a peer review system, where papers get accepted to journals, conferences, or other venues on the basis of reviews from other researchers, who ideally are subject area experts and thus are qualified to evaluate the paper. The reviewers also cannot have a conflict of interest with the authors, and should not be overwhelmed with too many papers to review. This is the ideal world, and is not always what happens in practice.

From my experience in the robotics academic community (and this may apply to other disciplines), it generally seems like there is no standard definition of an “appropriate” or “maximum” reviewing load for a reviewer. This is difficult to define as different papers mandate different reviewing efforts; a massive journal paper requires more time and effort than 2-3 page workshop papers. Furthermore, reviewing responsibilities can and should change depending on the progression of a researcher’s career. Consequently, this blog post serves to share my reviewing load. Hopefully I will continually update this post to better track (and limit) my reviewing load.

Here’s a detailed look at my reviewing load.

Based on Publication Venue

The standard publication venues for the robotics work that I do are ICRA, IROS, CoRL, RSS, and the IEEE RA-L journal, so most of my reviewing is concentrated there. Also, the “RA-L journal” is a bit nuanced in that papers can be submitted there with the option of a presentation at a conference such as ICRA, IROS, and CASE, hence why some researchers will write on their CVs and websites: “Paper published at IEEE RA-L with ICRA presentation option.” I am not counting such papers when I list ICRA, IROS, and CASE paper reviews.

The IEEE conferences have Associate Editors (AE). These are experienced researchers in charge of recruiting reviewers for papers and later recommending to accept or reject to senior editors. I served as an AE for the first time for IROS 2022.

IEEE conferences also allow for reviewer delegation, where one can technically be assigned to review a paper, but formally request someone else to fill it out. I am not counting those cases for my reviewing load.

Without further ado, here are the papers. When I list “papers in year X” that means that I reviewed them for the venue / conference that happens at that year (X). This might mean the actual reviewing happened the year before. For example, I reviewed ICRA 2023 papers in 2022, but I list them as “ICRA 2023” here. In other cases, such as CoRL, I review them the same year the papers are presented (since CoRL is near the end of the year). Of course, some (if not most) of the papers don’t get accepted.

• CoRL: 4 in 2020, 5 in 2021, 3 in 2022, 4 in 2023. AC duties: 9 in 2024.

• RSS: 3 in 2023, 4 in 2024. For workshops: 2 in 2020, 2 in 2021, both for the Visual Learning and Reasoning workshop.

• ICRA: 3 in 2020, 3 in 2021, 5 in 2022, 3 in 2023, 3 in 2024, 2 in 2025. For workshops: 6 in 2022, 6 in 2023, 11 in 2024. For workshop proposals: 1 in 2023, 2 in 2024, 1 in 2025.

• IROS: 1 in 2019, 3 in 2020, 4 in 2021, 2 in 2022, 2 in 2023, 3 in 2024. AE duties: 8 in 2022, 5 in 2023, 7 in 2024.

• CASE: 1 in 2018, 1 in 2019, and 1 in 2021.

• ISRR: 2 in 2022.

• IEEE TASE: 1 in 2022, 1 in 2023.

• IEEE RA-L: 2 in 2021, 4 in 2022, 2 in 2023, 4 in 2024. AE duties: 6 in 2024.

• IEEE T-RO: 1 in 2021, 2 in 2022. (These can be very long papers.)

• IJRR: 1 in 2023. (These papers can also be quite long.)

• AURO: 1 in 2023. (This refers to Autonomous Robots.)

• NeurIPS: 4 in 2016 (see my ancient blog posts here and here), though I’ve never been asked again (!). I did some workshop paper reviewing: in 2020, I reviewed 3 workshop papers for the Offline RL workshop, and in 2021 I reviewed 3 workshop papers, two for the Offline RL workshop (again) and one for the Safe and Robust Control workshop.

• ICML: just 1 workshop paper in 2023.

Based on Year

This list begins in 2019, since that’s when I started getting a lot of reviewing requests (and also publishing more papers, as you can see from my Google Scholar account).

To be clear, and as I said at earlier, these are how many papers I reviewed during that calendar year. For example ICRA is in the late spring and early summer most years, but the reviewing happens the prior fall. Thus, I would list papers I reviewed for ICRA 2020 in 2019 (not 2020) in the list below. In contrast, reviewing ICRA workshop papers happens the same year when the conference happens. I hope this is clear.

• 2019: total of 5 conference papers = 1 (IROS 2019) + 1 (CASE 2019) + 3 (ICRA 2020).

• 2020: total of 10 conference papers = 3 (IROS 2020) + 4 (CoRL 2020) + 3 (ICRA 2021), 5 workshop papers = 2 (RSS 2020) + 3 (NeurIPS 2020).

• 2021: total of 15 conference papers = 4 (IROS 2021) + 1 (CASE 2021) + 5 (CoRL 2021) + 5 (ICRA 2022), 3 journal papers = 2 RA-L + 1 T-RO, 5 workshop papers = 2 (RSS 2021) + 3 (NeurIPS 2021).

• 2022: total of 10 conference papers = 2 (IROS 2022) + 2 (ISRR 2022) + 3 (CoRL 2022) + 3 (ICRA 2023), 7 journal papers = 4 RA-L + 2 T-RO + 1 TASE, 6 workshop papers = 6 (ICRA 2022), 8 AE papers for IROS 2022, 1 workshop proposal for ICRA 2023.

• 2023: total of 12 conference papers = 3 (RSS 2023) + 2 (IROS 2023) + 4 (CoRL 2023) + 3 (ICRA 2024), 7 journal papers = 4 RA-L + 1 IJRR + 1 TASE + 1 AURO, 7 workshop papers = 6 (ICRA 2023) + 1 (ICML 2023), 5 AE papers for IROS 2023, 2 workshop proposals for ICRA 2024.

• 2024: total of 9 conference papers = 4 (RSS 2024) + 3 (IROS 2024) + 2 (ICRA 2025), 2 journal papers = 2 RA-L, 14 workshop papers = 11 (ICRA 2024) + 3 (IROS 2024), 22 AE/AC papers = 7 (IROS 2024) + 6 (RA-L) + 9 (CoRL 2024), 1 workshop proposal for ICRA 2025.

Above, I don’t list the journals with their year attached to them (i.e., I don’t say “IJRR 2023”) but I do that for the conferences and workshops. Hopefully it is not too confusing.

Reflections

What should my reviewing limit be? Here’s a proposed limit: 18 papers where:

• Conference papers and short journal papers count as 1 paper.
• Long journal papers (say, 14+ pages) count as 2 papers.
• Associate Editor papers count as 0.5 papers.
• Workshop papers count as 0.33 papers.
• Workshop proposals count as 0.33 papers.

As you might be able to tell from my heuristic calculations above, I think the research community needs a clear formula for how much each paper “costs” for reviewing. Also, I have been exceeding my limit, both in 2022 and in 2023.

As of late 2022, my average reviewing time for a “standard” conference paper with 6-8 pages is about 1.5 hours, from start to finish, which is way faster than my first efforts at reviewing. The average length of my reviews is on the higher end; typically it will fill up at least two full pages on Google Docs, with the default Arial 11-point font.

Also I am amazed at the effort that goes into rebuttals for CoRL and for journals like RA-L. I like the idea of rebuttals in theory, but the problem is as a reviewer, I feel that I expended so much effort in my initial review that I have little energy left over to read rebuttals.

When authors have papers rejected and then re-submit to a later venue, it is possible for that paper to get assigned to the same reviewers. As a reviewer, I have experienced this two times. To state the obvious: it is a lot better to resubmit papers with the recommended reviewer improvements, rather than resubmit the same PDF and hope the random sampling of reviewers gives a good draw.

I am curious about what others in the community consider to be a fair reviewing load.

I stand with Ukraine and firmly oppose Vladimir Putin’s invasion.

If someone were to counter and ask me with “What about when $X$ did this awful thing?”, I would urge that person to consider the direct human suffering of the current attack. Is the current invasion justified by any means?

And yes, I would also oppose similar military invasions against other countries, governments, and people – even those that happen to be just a fraction as severe as this one.

And yes, this is especially if $X$ refers to my home country.

A few resources that might help:

• Voices of Children
• The Kyiv Independent
• Kenya’s Response to Russia
• Garry Kasparov’s recommendations
• Volodymyr Zelenskyy’s speech to Russia
• List of charities (The Hill)
• Recommendation from Vlad Mnih (of DeepMind)

I welcome information about any other resources.

At the end of every year I have a tradition where I write summaries of the books that I read throughout the year. Here’s the following post with the rough set of categories:

• Popular Science (6 books)
• History, Government, Politics, Economics (6 books)
• Biographies / Memoirs (5 books)
• China (5 books)
• COVID-19 (2 books)
• Miscellaneous (7 books)

I read 31 books this year. You can find the other blog posts from prior years (going back to 2016) in the blog archives.

Books with asterisks are ones that I would especially recommend.

Popular Science

This also includes popular science, which means the authors might not be technically trained as scientists.

• Who We Are and How We Got Here: Ancient DNA and the New Science of the Human Past (2018) is by famous geneticist and Harvard professor David Reich. Scientific advances in analyzing DNA have allowed better analysis of human population migration patterns. The prior model of humans migrating out of Africa and to Europe, Asia, and the Americas in a “tree-like” fashion is out of date. Instead, mixture is fundamental to who we are as populations have migrated and mixed in countless ways. Also, ancient DNA can show the genetic percentage of an ancient population (including Neanderthals) in modern-day populations. A practical benefit from these studies is the ability to identify population groups as more at risk to certain diseases to others, but as Reich is careful to point out there’s a danger in that such studies can be exploited to nefarious means (e.g., racial stereotypes). I believe Reich’s justifications for working in this field make sense. If scientists try to avoid the question of whether there might be the slightest possibility of genetic differences among different populations, then the resulting void will be filled by racist and pseudo-scientific thinkers. Reich shows that the heavy mixture among different populations shatters beliefs held by Nazis and others regarding “pure races.” Science, when properly understood, helps us better respect the diversity of humans today.

• Kindred: Neanderthal Life, Love, Death and Art (2020) by Rebecca Wragg Sykes summarizes what researchers believe about Neanderthals, a species very closely related to Homo Sapiens (i.e., modern humans) who lived many thousands of years ago primarily in Europe and Asia. Neanderthals captivate our imagination since they are so much like ourselves. In fact, interbreeding was possible and did happen. But at some point, Neanderthals went extinct. Kindred reviews the cutting-edge science behind what Neanderthals were like: what did they eat, how did they live, where did they migrate to, and so on. (I was pleased to see that some of this information was also in David Reich’s book Who We Are and How We Got Here.) The main takeaway I got is that we should not view Neanderthals as a “less intelligent” version of modern humans. The book is a nice overview, and I am amazed that we are able to deduce this much from so long ago.

• Breath: The New Science of a Lost Art (2020) by James Nestor is about breathing. We all breathe, but breathing is not taught or discussed as widely as diet or exercise. Nestor describes an experiment where he stuffed his nose and was forced to mouth-breathe for 10 days. The result? Higher blood pressure, worse sleep, and a host of other adverse effects. Nestor also interviews historians, scientists, and those knowledgeable about breathing, to learn why humans have changed breathing habits for the worse, resulting in crooked teeth, worse sleep, and so on. The book concludes with some breathing advice: nose breathing, chewing, holding your breath, and suggesting certain breathing strategies. Written instructions for breathing can be hard to follow, so Nestor has a website with more information, including videos and additional expert advice. I’m not sure how much I will directly benefit from this book, given that I was already a strong nose-breather, and I don’t believe I suffer from snoring or sleep apnea — any sleep issues I might have are likely due to either (a) looking at too many screens (phones, laptops, etc.), or (b) thinking about the state of the world while my brain cannot calm down. It also feels like the book might over-exaggerate breathing, but to his credit, Nestor states that breathing is not going to cure everything. At the very least, it was nice to see a reaffirmation of my basic breathing habits, and I had not thought too much of my breathing habits before reading Breath.

• ** What To Expect When You’re Expecting Robots: The Future of Human-Robot Collaboration ** (2020) by Laura Major and Julie Shah. The authors are roboticists, and I am familiar with Julie Shah’s name (she’s a Professor at MIT) and her research area of human-robot interaction.¹ This book frequently refers to aviation, since it was one of the fields that pioneered a balance between humans and automation (robots) in real time in a safety-critical setting. In what cases does the aviation analogy hold for robots interacting with humans on the ground? As compared to aviation settings, there is a wider diversity of things that could happen, and we do not have the luxury that aviation has with highly trained humans paired with the robot (plane); we need robots that can quickly interact with everyday people. The authors present the key concept of affordances, or designing robots so that they “make sense” to humans, similar to how we can view a variety of mugs but immediately understand the function of the handle. Thinking about other books I’ve read in the past, the one that comes closest to this is Our Robots, Ourselves where MIT Professor David Mindell discussed the history of aviation as it pertains to automation.

• Think Again: The Power of Knowing What You Don’t Know (2021) is Adam Grant’s third book, following Give and Take and Originals, all of which I have read. At a time when America seems hyper-polarized, Grant shows that it is possible and better for people to be willing to change their minds. Think Again is written in his usual style, which is to present a psychological concept and back it up with research and anecdotes. Grant cites the story of Daryl Davis, a Black musician who has successfully convinced dozens of former Ku Klux Klan members to abandon their prior beliefs. While Grant correctly notes that it shouldn’t be the sole responsibility of Black people like Davis to take the lead on something like this, the point is to show that such change is possible.² Grant also mentions Harish Natarajan, an expert debater who effectively argued against a computer on a topic where he might naturally start off on the weaker end (he was asked to oppose “should we have universal preschool?”), and how Natarajan was able to force Grant to rethink some of his beliefs. Being willing to change one’s mind has, in theory, the benefit of flexibility in adapting to better beliefs. Overall, I think the book was reasonable. I try to assume I am open to revising beliefs, and remind myself this: if I feel very strongly in favor of anything (whether it be a political system, a person, a hypothesis, and so on) then I should be prepared to present a list of what would cause me to change my mind. Doing that might go a long way to reduce tensions in today’s society.

• ** Genius Makers: The Mavericks Who Brought AI to Google, Facebook, and the World ** (2021) by journalist Cade Metz. He writes about AI, and I frequently see his name floated around in articles about AI. Genius Makers is about AI and Deep Learning, and where it’s going. There are four main parts: the rise of Deep Learning, successes and hype (think AlphaGo), turmoil and dangers (bias in AI, militarization of AI, etc.), and the future. Throughout the book, there are stories about the key players in AI. As expected, featured players include Geoff Hinton, Yann LeCun, Yoshua Bengio, Jeff Dean, Andrew Ng, and Fei-Fei Li. The key companies include Google, Facebook, OpenAI, Microsoft, and Baidu. I follow AI news regularly, and the book contains some Berkeley-related material, so I knew much of the books’ contents. Nonetheless, there was still new material. For example, I think just about everyone in AI these days is aware that Geoff Hinton is “The Man Who Didn’t Sit Down” (the title of the prologue) but I didn’t know that Google bid 44 million USD for his startup, beating out Baidu. While I really like this book, Genius Makers may have overlap with other AI books (see my prior book reading lists for some examples) such that those who don’t want to consume dozens of books about AI may prefer other options. However, this one probably contains the most information about how the key players have interacted with each other.

History, Government, Politics, Economics

• ** Stamped from the Beginning: The Definitive History of Racist Ideas ** (2016) is a massive book by historian and antiracist Ibram X. Kendi. The “stamped from the beginning” term comes from former US Senator Jefferson Davis, who stated this in 1860 as the rationale for the inequality of whites and blacks. Kendi presents the history of racial inequality, with a focus on how racist ideas have persisted in America. There are five parts, each centering around a main character: Cotton Mather, Thomas Jefferson, William Lloyd Garrison, W.E.B. du Bois, and Angela Davis. Throughout each chapter, Kendi emphasizes that it was not necessarily hatred of other races that led to racism, but instead, racist thinking helped to justify existing racial disparities. He also frequently returns to three key ideas: (1) segregationst thought, (2) assimilationist thought, and (3) antiracist thought. While (1) seems obviously racist, Kendi argues that (2) is also racist. Kendi also points out inconsistencies in the way that people have treated people of different races. For example, consider Thomas Jefferson’s hypocrisy in criticizing interracial relationships, while he himself had sexual relationships with his (lighter-skinned) slaves, including Sally Hemingway.³ More generally it raises the question of the most important phrase in the Declaration of Independence, that “all men are created equal.” It is one that I hope we will continually strive to achieve.

• ** How Democracies Die ** (2018) is a well-timed, chilling, concise, and persuasive warning of how democracies can decay into authoritarianism. It’s written by Harvard Professors Steven Levitsky and Daniel Ziblatt, who specialize in democracies in Europe and Latin America. During the Cold War, democracies often died in the hands of military coups. But nowadays, they are dying in a more subtle way: by elected officials who use the system to subvert it from within. Those trends in America were developing for years, and burst in 2016 with the election of Trump, who satisfies the warning signs that Levitsky and Ziblatt argue are indicative of authoritarianism: (1) weak commitment to democratic rules of the game, (2) denial of the legitimacy of political opponents, (3) toleration or encouragement of violence, (4) readiness to curtail civil liberties of opponents, including media. Levitsky and Ziblatt argue that it’s not the text of the US Constitution that helped American democracy survive for years, as other countries have copied the US Constitution but still decayed into authoritarian rule. Rather, it’s the enforcement of democratic norms: mutual toleration and institutional forbearance. They review the history of America and cite historical events showing those democratic norms in action (e.g., stopping FDR’s court packing attempt), but admit that the times when democratic norms appeared more robust in America were at the same times when the issue of racism was de-prioritized. They ultimately hope that a multi-racial democracy can be combined with democratic norms. The book was written in 2018, and while they didn’t directly predict the COVID-19 pandemic, which may have exacerbated some anti-democratic trends (for example, by inhibiting the ability of government to function), Levitsky and Ziblatt were on the money when it comes to some of their authoritarian predictors. Trump suggesting that the election could be delayed? Yes. The refusal of many politicians to accept the results of the 2020 election (highlighted by the insurrection of 01/06)? Yes. How Democracies Die reminds me of The Fifth Risk where an equally prescient Michael Lewis wrote about the dangers of what happens when people in government don’t understand their duties. A commitment to democratic norms must be considered part of an elected official’s duties. I will keep this in mind and urge America towards a more democratic future. I don’t want to live in an authoritarian country which curtails free religion, free speech, an independent media, an independent judiciary, and where one man does the decision-making with insufficient checks and balances.

• Learning from the Germans: Race and the Memory of Evil (2019) by Susan Neiman, a Jewish woman, born in 1955, who has been a philosophy professor in the United States and Israel, and has also lived in Germany. I saw this listed in the recommended reading references in a Foreign Affairs magazine. Learning from the Germans consists of (1) Germany’s history of confronting its Nazi past, (2) America’s history of reckoning with slavery, and (3) a discussion over monuments, reparations, and what the future may hold for America and other countries that have to face prior sins. I learned about the complex and uneven path Germany took towards providing reparations to Jews, removing Nazi memorials, and so on, with East Germany handling this process better than West Germany. Neiman believes that Germany has responded to its past in a better way than the United States (with respect to slavery).⁴ It’s intriguing that many of the Germans who Neiman interviewed as part of her research rejected the title of the book, since they were ashamed of their country’s past, and surprised that others would want to learn from it. Neiman says it’s complicated to develop “moral equivalences” between events, but that ultimately what matters is how we address our past. If I were to criticize something happening in country “X”, and someone from that country were to respond back to me by criticizing America’s past sins, my response would be simply: “yes, you’re right, America has been bad, and here is what I am doing to rectify this …”. It’s not a contradiction to simultaneously hold the following beliefs, as I do, that: (1) I enjoy living in America, and (2) I am very cognizant and ashamed of many historical sins of America’s past (and present).

• ** Good Economics for Hard Times ** (2019) by Nobelists Abhijit Banerjee and Esther Duflo, both of MIT (and a married couple); see the announcement video shortly after they won the prize. They give a wonderful tour of topics in economics, but also clarify that it’s not clear which policies directly lead to growth, as traditionally measured in GDP. Much of the book emphasizes that there’s so much uncertainty in economics, and that given climate change, it might not be prudent to try to find the formula to maximize GDP. Rather, the goal should be to best address policies that can serve the poor and disadvantaged. Good Economics for Hard Times simultaneously was a fast read but also one that felt like it got enough of the technical information through to me. It’s not super likely to change the mind of growth-obsessed people, and it comes with some critique of Trump-style Conservatism. I think it was a great book for me, and one of my favorites this year.

• ** The Code: Silicon Valley and the Remaking of America ** (2019) is by Margaret O’Mara, a Professor of History at the University of Washington who researches at the intersection of technology and American politics. Hence, she is the ideal person to write this kind of book, and I have high interest in the subject area, since my research is in robotics and AI more broadly, the latter of which is the topic of interest in Silicon Valley today. O’Mara starts at the end of World War II, when the leaders in tech were on the East Coast near Boston and MIT. Over the next few decades, the San Francisco Bay Area would develop tremendously and by the 1980s, would surpass the East Coast in becoming the undisputed tech capital of the world. How this happened is a remarkable story of visionaries who began tech companies, such as Steve Jobs, Mark Zuckerberg, Sergey Brin, and Larry Page (and Bill Gates and Jeff Bezos up north in Seattle, though all have heavy connections with Silicon Valley) and venture capitalists like John Doerr. However, and perhaps this is the less interesting part, the story of Silicon Valley is also one of sufficient government funding for both companies and universities (notably, Stanford University), along with immigration from talented foreigners across the world, resulting in what O’Mara calls an “only-in-America story” made possible by broader political and economic currents. O’Mara is careful to note that this prosperity was not shared widely, nor could it truly be called a true meritocracy given the sexism in the industry (as elaborated further in Emily Chang’s Brotopia) and that wealth went mainly to the top few white, and then Asian, men. O’Mara brilliantly summarizes Silicon Valley’s recent history in a readable tome.

• ** The World: A Brief Introduction ** (2020) is by Richard Haass, president of the Council on Foreign Relations, which is my go-to think tank for foreign affairs. I started this book and couldn’t stop myself from finishing. It’s definitely on the side of breadth instead of depth. It won’t add much to those who are regular readers of Foreign Affairs, let alone foreign policy experts; Haass’ goal is to “provide the basics of what you need to know about the world, to make you more globally literate.” The book begins with the Treaty of Westphalia in 1648, which encoded the concept of the modern international system governed by countries. Obviously, it didn’t end up creating permanent peace, as the world saw World War I, World War II, the Cold War, and then the period after the Cold War up to today, which Haas said will later be given a common name by historians upon consensus. My favorite part of the book is the second one, which covers different regions of the world. The third part is the longest and covers challenges of globalization, terrorism, nuclear proliferation, climate change, and so on. The last one is broadly titled “order and disorder.” While I knew much of the material in the book, I was still able to learn aspects about worldwide finance and trade (among other topics) and I think The World does a valuable service in getting the reader on a good foundation for subsequent understanding of the world.

Biographies / Memoirs

• ** Shoe Dog: A Memoir by the Creator of Nike ** (2016) by Phil Knight, currently a billionaire and Nike cofounder, with Bill Bowerman. Each chapter describes a year (1962 through 1980) in Phil Knight’s early days in Oregon, where he co-founded Blue Ribbon Sports (later, Nike). Shoe Dog — named after the phrase describing people who know shoes and footwear inside out — is refreshingly honest, showing the challenges Knight faced with getting shoes from factories in Japan. Initially they relied on Onitsuka, but Nike had a protracted legal challenge regarding distribution rights and switched suppliers. Furthermore, Knight had a tough time securing funding and loans from banks, who didn’t believe that the company’s growth rate would be enough to pay them back. Knight eventually relied on Nissho⁵, a Japanese guarantor, for funds. Basically, the cycle was: get loan from Nissho, make sales, pay back Nissho, and repeat. Eventually, Nike reached a size and scope comparable to Adidas and Puma, the two main competitors to Nike at that time. Nowadays, things have probably changed. Companies like Uber continually lose money, but are able to get funding, so perhaps there’s more of a “Venture Capitalist mentality” these days. Also, I worry if it is necessary to cut corners in business to succeed. For example, in the early days, Knight lied to Onitsuka about having an office on the east coast, and after signing a contract with Onitsuka, Knight had to scramble to get a factory there! Things have to be different in today’s faster-paced and Internet-fueled world, but hopefully the spirit of entrepreneurship lives on.

• ** Born a Crime: Stories from a South African Childhood ** (2016), by comedian Trevor Noah, was great. I’m aware of his work, though have never watched his comedy. He was “Born a Crime” as the son of a White (Swiss) father and a Black mother, which was illegal under South Africa’s apartheid system. Noah was Colored, and could not be seen with his mother in many places without the risk of police catching him. I realized (though I’m sure I was taught this earlier but forgot it) that in South Africa’s apartheid system, whites were actually a minority, but apartheid allowed whites to remain in control, and a key tactic was pitting different minority groups against each other, usually Blacks.⁶ Noah had a few advantages here, since he was multi-lingual and could socialize with different minority groups, and his skin color looked light on film at that time. For example, Noah a Black friend robbed a mall, and he was caught on video. When the school principals summoned Noah, they asked him if he knew who the “white” guy was in the video. The person was Noah, but the administrators were somehow unable to tell that, blinded by certain notions of race. Apartheid formally ended during Noah’s childhood, but the consequences would and still are reverberating throughout South Africa. I’m frankly amazed at what Noah overcame to be where he is today, and also at his mother, who survived attempts at near murder by an ex-husband. The answer isn’t more religion and prayer, it’s to remove apartheid and to ensure that police listen to women and properly punish men who commit domestic violence.

• The Ride of a Lifetime: Lessons Learned from 15 Years as CEO of the Walt Disney Company (2019) by Robert Iger is a readable book on leadership and business, and provides the perspective of what it is like being a CEO at a huge international company. The first half describes his initial career before being CEO, and the second half is about his experience as CEO. Iger describes the stress throughout the selection stage to see who would become CEO after Michael Eisner, and how Iger had to balance ambition of wanting the job without actually demanding it outright. There was also the complexity of how Iger was already a Disney insider before becoming CEO, and some wanted to bring in a fresh outsider. I enjoyed his view on Steve Jobs, especially after having read Walter Isaccson’s biography of Steve Jobs last year. (Jobs had a sometimes adversarial relationship with Disney.) It’s also nice that there’s “no price on integrity” (the title of Chapter 13) and that Iger is supportive of cracking down on sexual assault and racism. I have a few concerns, though. First, it seems like most of the “innovation” happening at Disney, at least what’s featured in the book, is based on buying companies such as Pixar and Lucasfilm, rather than in-house development. It’s great that Iger can check his ego and the company’s ego, but it’s disappointing from an innovation perspective. Second, while there is indeed “no price on integrity,” how far should businesses acquiesce to governments who place far more restrictions on civil liberties than the United States government? Iger also repeatedly emphasizes how lucky he was and how important it was for others to support him, but what about others who don’t have that luxury?

• ** The Great Successor: The Divinely Perfect Destiny of Brilliant Comrade Kim Jong Un ** (2019) by New Zealand journalist Anna Fifield. This book is extremely similar to the next book I’m listing here (by Jung H. Pak), so I’m going to combine my thoughts there.

• ** Becoming Kim Jong Un: A Former CIA Officer’s Insights into North Korea’s Enigmatic Young Dictator ** (2020) by Jung H. Pak, who used to work in the CIA and has since been at the Brookings Institution and in the US State department. I have to confess, my original objective was to read a biography of Xi Jinping. When I tried to search for one, I came across UC Irvine Professor Jeffrey Wasserstrom’s article in The Atlantic saying that there weren’t any good biographies of Xi.⁷ The same article then said there were two biographies of Kim Jong Un, and that’s how I found and read these two books. I’m glad I did! Both do a good service in covering Kim Jong Un’s life from North Korea royalty to Switzerland for school, then back to North Korea to get groomed for future leadership, followed by his current leadership since 2011. I vaguely remember when he first came to power, and seeing news reports questioning whether Kim Jong Un truly held power, since he was the youngest head of state at that time. But the last decade has shown that Kim’s grip on power is ironclad. There are only a few differences in the topics that the books cover, and I think one of them is that near the end of Becoming Kim Jong Un, Pak ponders about how to deal with the nuclear question. She argues that rather than do a misguided first strike like John Bolton once foolishly suggested in a WSJ op-ed just before he became the US National Security Advisor for former president Trump, we have to consider a more nuanced view of Kim and realize that he will only give up nuclear weapons if maintaining them comes at too great a cost to bear. Since the book was published, COVID-19 happened, and if there’s been any single event that’s caused more harm to North Korea’s economy, it’s been this, as exemplified by how Russian diplomats had to leave North Korea by hand-pushed rail. I still maintain my view that Kim Jong Un is one of the worst leaders alive today, and I hope that the North Korea situation can improve even a tiny bit in 2021.

China

• ** Factory Girls: From Village to City in a Changing China ** (2008) by Leslie T. Chang, who at that time was a journalist for the Wall Street Journal. I found out about this book when it was cited by Jeffrey Wasserstrom and Maura Cunningham in their book. Chang was motivated to provide an alternative perspective from a “traditional” American media, where a lot of the focus is on dissidents and human rights (not a bad thing per se, but it’s good to have balance). In this book, Chang meets and interviews multiple women who came from rural areas to work in factories, particularly those located in Dongguan, an industrial city in southern China in the Pearl River Delta region (a bit north of Hong Kong). As a reporter who also could speak in Mandarian, Chang is skillfully able to convey the women’s journey and life in a highly sympathetic manner. She does not sugarcoat the difficulties of living as a factory worker; the women who she interviews have to work long hours, might see friendships end quickly, and have difficulties finding suitable husbands in a city that has far more women than men. Factory Girls also contains Chang’s own exploration of her family history in China. While still interesting, my one minor comment is that I wonder if this might have diluted the book’s message. Despite the 2008 publication date, the book is still readable and it seems like the rural-to-urban shift in China is still ongoing.

• ** Deng Xiaoping and the Transformation of China ** (2011) is a massive history tome on the former Chinese leader by the great historian Ezra F. Vogel, a long-time professor at Harvard University. (He passed away in late 2020.) There likely are many other biographies of Deng and there may be more in the future, but Vogel’s book is considered the “definitive” one, and compared to later historians, Vogel will have had the advantage of interviewing Deng’s direct family members and associates. The reason for studying Deng is obvious: since Deng took over the reins of China in 1978 following Mao’s death in 1976 and a brief interlude afterwards, he led economic reforms that opened the world’s most populous country and helped to lift millions out of poverty. The bulk of the book covers Deng’s leadership from 1978 through 1992. This includes economic reforms such as the establishment of “Special Economic Zones,” allowing foreign investment, and sending students abroad, largely to the United States, which also benefits from this relation, as I hope my recent blogging makes clear. It also includes foreign affairs, such as the peaceful return of Hong Kong to China and the difficulties in reuniting China and Taiwan. As a recent NY Times obituary here states, a criticism of Vogel’s book is that he might have been too lenient on Deng in his reporting, I do not share that criticism. In my view the book presents a sufficiently comprehensive view of the good, bad, and questionable decisions from Deng that it’s hard for me to think of a harsh criticism.⁸ (It is true, however, that the Chinese government censored parts of this book for the Chinese translation, and that I dislike.) Vogel’s masterpiece is incredible, and I will remember it for a long time.

• ** China Goes Global: The Partial Superpower ** (2012) is by David Shambaugh, a professor at the Elliott School of International Affairs at the George Washington University (same department as Prof. Sean Roberts). From the 1978 reforms which opened the country up to 2012, China’s been massively growing and asserting its influence on the world, but is not yet a “superpower” as would be suggested based on its population and economy. This could be due to hesitancy in taking on greater international roles, as that might require expensive interventions and undertakings that could hinder its economic growth, which is the CCP’s main mandate to the Chinese people. One thing I immediately noticed: the book has the most amount of quotes, citations, or interviews with Chinese government officials or academics than any other book I’ve read. (This was the pre-Xi era and the country was generally more open to foreigners.) Shambaugh does a great job conveying the wide range of opinions of the Chinese foreign policy elite. Two of the most cited scholars in the book are Yan Xuetong and Wang Jisi, whose names I recognized when I later read Foreign Affairs articles from them. Another thing worth mentioning: Chinese officials have told Shambaugh that they believe the “Western” media is misinformed and does not understand China. Shambaugh recalls replying, what precisely is the misunderstanding, and the government officials were aghast that there could be any disagreement. In Shambaugh’s view, the media is tough but accurate on China.⁹ As Shambaugh emphasizes, so many people want to know more about China (myself included, as can be obviously inferred!), and in my view this means we get both the positive and the negative. This book is a great (if somewhat dated) survey, and helps to boost my personal study of China.

• China Goes Green: Coercive Environmentalism for a Troubled Planet (2020) is co-written by professors Yifei Li and Judith Shapiro. The focus in China Goes Green is to discuss the following: in today’s era of accelerating climate change (or climate crisis), is China’s authoritarian government system better suited to tackle environmental challenges? Some thinkers have posited that, while they may be sympathetic to liberal democracy and human rights, maybe the climate urgency of today means such debate and freedoms have to be set aside in favor of “quicker” government actions by authoritarian rule. Li and Shapiro challenge this line of reasoning. A recurring theme is that China often projects that it wants to address climate change and promote clean energy, but the policies it implements have the ultimate goal of increasing government control over citizens while simultaneously having mixed results on the actual environment. That is, instead of referring to China today as “authoritarian environmentalism”, the authors argue that “environmental authoritarianism” is more accurate. The book isn’t a page-turner, but it serves a useful niche in providing an understanding of how climate and government mesh in modern China.

• ** The War on the Uyghurs: China’s Campaign Against Xinjiang’s Muslims ** (2020) is by Sean Roberts, a professor at the Elliott School of International Affairs at the George Washington University (same department as Prof. David Shambaugh). The Xinjiang internment camps of China have become household names among readers of international news outlets, with reports of genocide and forced labor. Roberts explains the tense history between the ethnic Han majority in China versus the Turkic people who primarily live in the rural, western areas of the country. A key part of the book is precisely defining what “terrorism” means, as that has been the rationale for the persecution of the Uyghurs, and also other Muslim groups (including in the United States). Roberts covers the Urumqi riots and other incidents that deteriorated relations between Uyghurs and the Chinese government, and then this led to what Roberts calls a “cultural genocide” that started from 2017 and has continued today; Roberts recalled that he and other fellow academics studying the subject realized something was wrong in 2017 when it became massively harder to contact his colleagues from Xinjiang. One of the most refreshing things (in my view) is reading this knowledge from an academic who has long studied this history, instead of consuming information from politicians (of both countries) who have interests in defending their country,¹⁰ and Roberts is not shy about arguing that the United States has unintentionally assisted China in its repression, particularly in the designation of certain Muslim groups as “terrorism”. Of all the news that I’ve read in 2021, among those with an international focus, the one that perhaps stuck the most to my mind from 2021 is Tahir Izgil’s chilling story about how he escaped the camps in Xinjiang. While this is just one data point of many, I hope that in some way the international community can do what it can to provide refugee status to more Uyghurs. (I am a donor to the Uyghur Human Rights Project.)

COVID-19

• ** The Premonition: A Pandemic Story ** (2021) by Berkeley’s Michael Lewis is the second book of his I read, after The Fifth Risk (published 2018), which served as an unfortunate prologue for the American response to COVID-19; I remembered The Fifth Risk quite well after reading How Democracies Die earlier this year. I didn’t realize Lewis had another book (this one) and I devoured it as soon as I could. The US was ranked number one among all countries in terms of pandemic preparation. Let that sink in. By the time it was mid-2021, the US had the most recorded deaths of any country.¹¹ Lewis’ brilliance in his book, as in his others, is to spotlight unsung heroes, such as a California health care official and a former doctor who seemed to be more competent than the United States government or the Centers for Disease Control (CDC). Lewis is so good at connecting the reader with these characters, that when reading the book, and seeing how they were stopped and stymied at seemingly every turn from sluggish government or CDC officials, I felt complete rage. (The same goes for the World Health Organization, but the CDC is a US entity, so we have more ability to reform it.) The biggest drawback of this book is that Lewis doesn’t have any endnotes or details on how he went about investigating and interviewing the people in his book. In all fairness, the officials he criticizes in this book should have the opportunity to defend themselves. Given the way the CDC acted early in the pandemic, though, and the number of recorded deaths it would be surprising if they could mount effective defenses, but again, they should have the opportunity. One more thing, I can’t resist suggesting this idea: any current and future CDC director must have a huge sign with these words: You must do what is right for public health. You cannot let a politician silence or pressure you into saying what he or she wants. This sign should be right at the desk of the CDC director, so he/she sees this on a daily basis. Check out this further summary from NPR and some commentary by Scott Aaronson on his blog.

• ** World War C: lessons from the COVID-19 Pandemic and How to Prepare for the Next One ** (2021) is by CNN’s chief medical correspondent Dr. Sanjay Gupta, released in October 2021, and I expect it to reach a wide audience due to Dr. Gupta’s position at CNN. After a brief review of the early days of the pandemic, the book covers how diseases spread, the effects of COVID, and the function of vaccines. Then, it provides guidelines for building resilience to the next pandemic. For the most part, the writing here seems reasonable, and my main disappointment doesn’t really have to do with Dr. Gupta per se, but has to do with how understanding the effects of “long-haul COVID” is just going to take a lot of time and involve a lot of uncertainty. Also, and this may be a good (or not so good) thing but Dr. Gupta, while acknowledging that politics played a role in hindering the war against the pandemic (particularly in the US), tries to avoid becoming too political. His last chapter, on ensuring that humanity fights together, resonates with me. In April 2021, India was hit with a catastrophic COVID wave due to the delta variant, and at least one of Dr. Gupta’s relatives died. Since the virus constantly mutates, the world essentially has to be vaccinated against it at once to mitigate its spread. As the Omicron variant was spreading as I finished up this book near the end of the year, it’s imperative that we end up supporting humans throughout the world and give out as many vaccines as we can, which is one reason why I consider myself a citizen of the world.

Other

• Rest: Why You Get More Done When You Work Less (2016) by Alex Soojung-Kim Pang, emphasizes the need for rest and recovery to improve productivity. This seems obvious. I mean, can you really work 16 hours a day with maximum energy? Pang argues that it’s less common for people to think about “optimizing” their rest as opposed to things more directly related to productivity. As he laments: “we think of rest as simply the absence of work, not as something that stands on its own or has its own qualities.” The book presents anecdotes and studies about how some of the most creative and accomplished people (such as Charles Darwin) were able to do what they did in large part due to rest, or taking breaks such as engaging in long walks. Here’s an interview with the author in the Guardian. That said, while I agree with the book’s general thesis, it’s not clear if I actually benefited as much from reading this book as others. As I fine-tune this review in late December 2021, three months months after I finished reading this book, I’m not sure how much of the details I remember, but it could be due to reading other books that convey similar themes.

• ** Skin in the Game: Hidden Asymmetries in Daily Life ** (2018) by Nassim Nicholas Taleb is part of his 5-book “Incerto” series. I’ve only read this book and I might consider reading his other books. When someone has “Skin in the Game,” that person has something to lose. Consider someone making a prediction about what will happen in 2022 regarding COVID. If that person has to tie his or her prediction with significant financial backing and is thus at risk of losing money with a bad prediction, then there is “skin in the game,” in contrast to someone who can make an arbitrary prediction without being held accountable. The book is thus a tour of various concepts in life that tie back to this central theme, along with resulting “hidden asymmetries.” For example, one reason why Taleb is so against interventionism (e.g., the United States invading Iraq) is because it shows how so many foreign policy pundits could safely argue for such an invasion while remaining in the comfort of their suburban homes, and thus there’s an asymmetry here where decisions they advocate for don’t affect them personally too much, but where they affect many others. If you can get used to Taleb’s idiosyncratic and pompous writing style, such as mocking people like Thomas L. Friedman as not a “weightlifter” and insulting Michiko Kakutani, then the book might be a good fit as there’s actually some nice insights here.

• ** Measure what Matters: How Google, Bono, and the Gates Foundation Rock the World with OKRs ** (2018) by famous VC John Doerr describes the “OKR” system which stands for “Objectives and Key Results.” Doerr is revered throughout Silicon Valley and is known for mentoring Google founders Larry Page and Sergey Brin. I have prior experience interning at Google (remotely) in summer 2020, and I saw a few documents that had OKRs, though I never used the system much nor did I hear much about it, but I imagine that would change if I ever joined Google full-time. The book covers diverse examples of organizations that have used OKRs (not just those in big tech), and a common theme that comes up is, well, work on what matters. The goal should be to identify just a few key objectives that will make an impact, rather than try to optimize less-important things. It’s kind of an obvious point, but it’s also one that doesn’t always happen. While the message is obvious, I still think Doerr explains this with enough novelty to make Measure what Matters a nice read. I signed up for the corresponding email subscription, and there is also a website. Perhaps I should check those out if I have time. It might be good to map out a set of OKRs for my postdoc.

• Edge: Turning Adversity into Advantage (2020) by Harvard Business School Professor Laura Huang, acknowledges that all of us have some adversity, but that it is possible for us to turn this into something advantageous. That is better than just giving up and using adversity (e.g., “I grew up poor”) as an excuse to not do anything. Some of her suggestions involve trying to turn stereotypes into your favor (e.g., redirecting what people thought of her as an Asian female), and to see how unexpected behavior might be useful (e.g., as when she was able to get Elon Musk to talk to her). I think her message seems reasonable. I can imagine criticism from those who might think that this deprioritizes the role that systematic inequality play in our society, but Professor Huang makes it clear that we should also tackle those inequities in addition to turning adversity into advantage. The writing is good, though it sometimes reads more casually than I would expect, which I think was Professor Huang’s intent. I also enjoyed learning about her background: her family’s immigration to the United States from Taiwan, and how she became a faculty member at Harvard despite unexpected challenges (e.g., not graduating from a top PhD school with lots of papers). You can see a video summary of the book here.

• Breaking the Silence Habit: A Practical Guide to Uncomfortable Conversations in the #MeToo Workplace (2020) by Sarah Beaulieu, attempts to provide a guideline for challenging conversations with regards to anything that might be relevant to “MeToo.” She deliberately does not give firm answers to questions such as “can I date a work colleague” or “should I report to the manager” but emphasizes that it must be viewed in context and that there are different ways one can proceed. This might sound frustrating but it seems reasonable. Ultimately I don’t know if I got too much direct usage out of this since much of it depends on actually testing and having these conversations (which, to be clear, I fully agree that we should have), which I have not had too much opportunity to engage in myself.

• Skip the Line: The 10,000 Experiments Rule and Other Surprising Advice for Reaching Your Goals (2021), by serial entrepreneur and author James Altucher, uses the analogy of “skipping the line” for accelerating career progress, and not necessarily having to trudge through a long list of hierarchies or spend 10,000 hours practicing a skill (as per Malcolm Gladwell). He provides a set of guidelines, such as doing 10,000 experiments instead of 10,000 hours, and “idea sex” which is about trying to tie two ideas together to form new ones. My impression is that Altucher generally advocates for regularly engaging in (smart) risks. I won’t follow all of this advice, such as when he argues to avoid reading news in favor of books (see my information diet), but I think some ideas here are worth considering for my life.

• ** A World Without Email: Reimagining Work in an Age of Communication Overload ** (2021) is another book by Cal Newport, and surprise surprise, one that I also enjoy (see my prior reading lists). I would say “I don’t know how he publishes all these books” but in his case, we do know how since the answer lies in this and his past books (even if it’s not easy to implement). Newport’s key argument that email started off as a way to facilitate easier communication, but it soon created what he calls the “hyperactive hive mind” world, characterized by being in a state of constant online presence, checking email and other messaging platforms (e.g., Slack) throughout the day (and in the evening, and on weekends…). Newport makes a convincing case that this is reducing productivity and making us miserable. For example, he makes the obvious argument that a short face-to-face conversation can better clarify information compared to many back-and-forth emails that sap time and attention away from things that produce actual value. In the second part of the book, he proposes principles for operating in a world without (or realistically, less) email. I thought these were well-argued and are anti-technology; it’s a way of better using technology to create more fulfilling lives. I still think I check email too much but I enjoy the days when I can simply work and program all the way, and only check email starting around 4:00PM or so. As usual I will try to follow this book’s advice, and I think even doing this moderately will help my work habits in an increasingly online world given the pandemic.

This is a regularly updated post, last updated July 16, 2023.

On July 03 2021, the subject of media and news sources came up in a conversation I had with someone over brunch when we were talking about media bias. I was questioned by that person: “what news do you read?” I regret that I gave a sloppy response that sounded like a worse version of: “uh, I read a variety of news …” and then I tried listing a few from memory. I wish I had given a crisper response, and since that day, I have thought about what that person has asked me every day. Yes, literally every day.

In this blog post, I describe my information diet, referring to how I read and consume media to understand current events. Before getting to the actual list of media sources, here are a few comments to clarify my philosophy and which might also preemptively address common objections.

• There are too many sources and not enough time to read all the ones I list in detail every day. Instead I have to be strategic. If I find that I haven’t been checking one of these sources for a few days, then I mentally mark it down as a “TODO” to catch up on reading it in the near future. Another reading strategy is that I check news during a limited time range in the evening, after work, so that I am not tempted to browse these aimlessly all day. Otherwise, I would never get “real” world one. I also prefer reading over watching, as I can cover more ground with reading.

• I did not list social media style sources such as Reddit and Twitter. I get some news from these, mainly because my field of robotics and AI strangely relies on Twitter for promoting academic content, but I worry that social media is designed to only amplify voices that we believe are correct, with algorithms funneling us towards information to which we are likely to agree, which increases polarization. Furthermore, especially when people can post anonymously, discussions can get highly charged and political. That brings me to the next point…

• Whenever possible, look for high quality reporting. A few signals I ask myself in regards to this: (1) Are there high standards for the quality of reporting, and does the writing appear to be in-depth, detailed, empathetic, and persuasive instead of hyper-partisan and filled with ad-hominem attacks? (2) Can I verify the identity of the authors? (3) Who are the experts that get invited to provide commentary? (4) Do articles cite reputable academic work? (5) Are there easily-searchable archives to make sure that whatever people write is written in the permanent record?

• I also strive to understand the beliefs behind the people who own and fund the media source. In particular, can the media be critical of the people who fund it, or the government where its headquarters is geographically located? How much dissent is allowed? I am mindful of the difference between an opinion article versus an article that describes something such as a natural disaster. While both have bias, it is more apparent in the former since it’s by definition an opinion.

• Regarding bias, in my view every newspaper or media source has some set of bias (some more than others) which reflects the incentives of its organizers. Every person has bias, myself included naturally, which explains why I get suspicious whenever someone or an entity claims to be the sole arbiter of truth and “unbiased” and so on. Thus, when I read a newspaper — say a standard corporate newspaper in the United States — I consume its content while reminding myself that the choices of articles and reporting reflect biases inherent in the paper’s executives or organizers. Similarly, when I read from a source that’s partially or fully in control of a government, I keep a reminder to myself that such media ultimately has to protect the interests of its government.

• This does not mean it is a bad idea per se to consume biased media. My main argument is that it is a bad idea to consume a small set of media that convey highly similar beliefs and messages. (I also think it is a bad idea to consume no media, as if the solution to avoiding bias is to avoid the news altogether. How else would I be able to know what goes on in the world?) I am also not saying that reading from a variety of media sources is a “solution” or a “cure” for biased news media; my claim is that it is better than the existing alternative of only limiting oneself to a small set of tightly similar media.

• This means that, indeed, I read from media sources whose beliefs I might find to be repugnant or misguided. Maybe it’s just a weird peculiarity of myself, but I like reading stuff that causes me to get into a rage. If anything, seeing how particular sources try to frame arguments has made it a lot easier for me to poke holes through their reasoning. In addition, people I disagree with are sometimes … not entirely wrong. I can strongly disagree with the political beliefs of a writer or broadcaster, but if they write an 800-word essay on some narrow issue, it may very well be that I agree with the contents of that essay. Of course, maybe they are wrong or misleading, in which case it’s helpful to cross-reference with other media sources.

• I have lost count of the number of times I have read variations of: “what the media doesn’t want to tell you …” or “the media doesn’t cover this…” or “the media is heavily biased…”. I’m not sure it’s possible to collectively assume that all the sources I list below are heavily biased together. They each have some bias on their own, but can all of them really be collectively biased against one entity, individual, government, or whatever? I don’t believe that’s the case, but let me know if I’m wrong. My guess is that when people say these things, they’re referring to a specific group of people who consume a narrow subset of media sources. (Interestingly, when I read those variations of “the media doesn’t want you to know…” it’s also self-defeating because I have to first read that phrase and its associated content from a media source in the first place.) The bigger issue might be consuming media from too few sources, instead of too many sources.

• I don’t pay for most of these sources. Only some of these require subscriptions, and it might be possible to get subscriptions for free as part of a job perk, or to get a discount on the first year of the purchase. I will not pay for a newspaper if it is government-funded, but it’s typically a moot point because those types of newspapers tend to make all their content “freely” accessible (since it would, of course, be in the funding government’s interests to maximize such dissemination). As of July 2023, I now list my (approximate) subscription payments.

• Nonetheless, I highly encourage paying and supporting local newspapers. For reference, I used to own a subscription to the Pittsburgh Post Gazette when I lived in Pittsburgh, and before that I read Berkeleyside (and donated on occasion) since I did my PhD at Berkeley. A local newspaper will tend to have the most accurate reporting for local news. Furthermore, if there is concern about bias in national news or if (geo)politics feels depressing, then local news tends to cover less of that.

• I also encourage supporting press freedom. I fully recognize that I am fortunate to have the freedom to read all these sources, which I deliberately chose so that they cover a wide range of political and worldwide views. This freedom is one of the greatest and most exhilarating things about my wonderful life today.

Without further ado, here are some of the media sources (there is some logic to the ordering). If a news source is listed here, then I can promise you that while I can’t spend equal amounts of time reading each one, I will make an honest effort to give the source sufficient attention.

• CNN
• CNBC / MSNBC
• FOX
• NPR
• Bloomberg
• The Guardian
• New York Times [subscriber, about $20/month]
• Los Angeles Times [subscriber, about $5/month]
• Wall Street Journal [subscriber, about $15/month]
• USA Today
• The Washington Post
• Politico
• FiveThirtyEight
• Inside Climate News [occasional donor]
• National Review
• Newsweek
• The Atlantic
• ProPublica
• Vox
• Wired
• The Information
• ESPN
• The Points Guy
• BBC
• Reuters
• Israel Hayom
• Al Jazeera
• The Tehran Times
• The Kyiv Independent [patreon, about $5/month]
• The Moscow Times
• Russia Today
• China Daily
• South China Morning Post
• Taipei Times
• The Korea Herald
• The Hoover Institute
• Cato Institute
• The Council on Foreign Relations / Foreign Affairs [subscriber, about $50/year]
• Amnesty International

I hope this list is useful. This blog post is the answer that I will now give to anyone who asks me about my information diet. As always, I look forward to your criticism. :-)

Changelog:

July 16, 2023: due to my current living situation, I removed the Pittsburgh Post Gazette, Berkeleyside, and the San Francisco Chronicle, and I added the Los Angeles Times to my reading list. I also removed ABC because even though I might log into it now and then, it isn’t part of my critical reading mass. I also added The Information since I frequently get email updates from them with a summary of their major news; I will consider formally subscribing to them. Finally, for full transparency, I indicate in the list which news sources I fund or pay to read.

Lately, I have been in touch with some of the political offices for whom I am a constituent, to ask if they can consider steps that would improve the climate for Chinese international students and scholars. Now that I reside in the critical swing state of Pennsylvania, the two US Senators who represent me are Senators Bob Casey and Pat Toomey. This past week, I called their Pitttsburgh offices multiple times and was able to contact a staff member for Senator Toomey.

What follows is a rough transcript of my conversation with the staff member. This is from memory, so there’s obviously no way that this is all correct, and it’s also a sanitized version as I probably got rid of some ‘uhms’ or mumbles that I experienced when having this conversation. However, I hope I was able to deliver the main points.

[Begin Transcript]

Me: Hello, is this the office of Senator Pat Toomey?

Staff Member: Yes it is, how may I help you?

Me: Thank you very much for taking my call. My name is Daniel, and I am a researcher at Carnegie Mellon University in Pittsburgh, working in robotics. I wanted to quickly talk about two main points.

Staff Member: Sure.

Me: First, I’m hoping to talk about something called the China Initiative. This is something that President Trump started and President Biden has continued. This is causing some concerns among many of us in the scientific research community, especially among those from China or even ethnic Chinese citizens of other countries. Essentially this is trying to see if there’s hostile intentions among researchers or if there are undisclosed connections with the Chinese government. Right now it seems to be unfairly targeting Chinese researchers, or at the very least assuming that there is some form of guilt associated with them. If there’s anyway we can look at ending, or at least scaling back this initiative, that would be great. A bunch of leading top American universities have asked our Attorney General to consider this request, including I should also add, Carnegie Mellon University.

Staff Member: Yes, I understand.

Me: And so, the other thing I was hoping to bring up is the subject of visas. Many of my Chinese colleagues are on 1-year visas, whereas in the past they might have gotten 5-year visas. If there’s any way we can return to giving 5-year visas, that would be great. It makes things easier on them and I think they would appreciate it and feel more welcomed here if they had longer visas.

Staff Member: I see.

Me: To be clear, I’m not discounting the need to have security. I fully understand that there has to be some layer of security around international scholars, and I also understand the current tensions between the two governments involved. And I personally have major disagreements with some things that the government of China has been doing. However, what I’m saying is that we don’t necessarily want to assume that Chinese students feel the same way, or at least, we don’t want to treat them under a cloud of suspicion that assumes they have malicious intents, with guilt by assocation.

Staff Member: Yes, I see.

Me: And more on that point, many of the Chinese students end up staying in this country out of their own desires, some of them end up staying as professors here, which overall helps to increase research quality. Or they might stay as entrepreneurs … this helps out the local community here as well.

Staff Member: Sure, I understand your concerns. This seems reasonable, and I can pass your concerns to Senator Toomey. First, may I have your last name? I didn’t quite catch that.

Me: My last name is Seita. It’s spelled ‘S’ as in … uh, Senator, ‘e’, ‘i’, ‘t’, ‘a’.

Staff Member: Thanks, and what is your phone number and address?

Me: [I provided him with this information.]

Staff Member: And what about your email?

Me: It’s my first letter of the first name, followed by my last name, then ‘at’ andrew dot cmu dot edu. This is a CMU email but it has ‘andrew’ in it, I think because of Andrew Carnegie.

Staff Member: Oh! [Chuckle] I have a number of contacts from CMU and I was always wondering why they had emails that contained ‘andrew’ in it. Now I know why!

Me: Oh yeah, I think that’s the reason.

Staff Member: Well, thank you very much. I also know that Senator Toomey will be interested in these two items that you brought up to me, so I will be sure to pass on your concerns to him, and then he can reply to you.

Me: Thank you very much.

[End Transcript]

The staff member at Pat Toomey’s office seemed sincere in his interest in passing on this information to Senator Toomey himself, and I appreciate that. I am fairly new to the business of contacting politicians but hopefully this is how US Senators get word of what their constituents think.

Update December 24, 2021: Since my original conversation above, I’ve continued to contact Pennsylvania’s US Senators along with my US Representative. Senator Pat Toomey and Senator Bob Casey, along with Representative Mike Doyle, have forms on their website where I can submit emails to voice my concerns. Here’s the email template I used for contacting these politicians, with minor variations if needed:

Hello. My name is Daniel and I am a robotics researcher at Carnegie Mellon University. I wanted to ask two quick requests that I hope the Senator and his staff can investigate.

The first is the China Initiative, designed to protect America against Chinese espionage. I fully understand and respect the need for national security, and I am highly concerned about some aspects of the current government of China. However, this initiative is having a negative effect on the academic community in the United States, which by its very nature is highly international. What we don’t want to do is assume without direct evidence that Chinese researchers, or researchers who appear to be ethnic Chinese, or researchers who collaborate with those from China, have nefarious intentions. A bunch of leading American universities have asked Attorney General Merrick Garland to take a look at scaling back, limiting, or eliminating outright the China Initiative, which has been continued under President Biden. If you can take a look at that, that would be great. For more context, please see: https://www.apajustice.org/end-the-china-initiative.html

The second is about visas. If someone from the Senator’s staff can take a look at visas for Chinese international students, and particularly consider giving them 5 year visas instead of the 1 year visas that are becoming more common now. In the past, Chinese students have told me that they got 5-year visas, and a longer visa would make travel easier for them and would make them feel more welcomed to the country. We get a lot of Chinese students and other international students, and one reason why top American universities are the best in the world is because of talent that gets recruited across the world. Many of the Chinese students additionally end up staying in the United States as professors, entrepreneurs, and other highly-skilled employees, which benefits our country. If they wish to stay, I hope we can be as welcoming as possible. And if they choose to return to their home country, then the more welcoming we are, the more likely they might be to pass on positive words to their colleagues, friends, and family members.

Thank you for your consideration.

(Unfortunately, Representative Doyle’s website seems to not be functioning properly and I got a “The Requested Page Could Not Be Found” error, so I might need to call his office. However, I also got an automated email response thanking me for contacting his office … so I’m not sure if his office got my message? I will investigate.)

A few days later, Senator Casey’s office responded with an email saying that my message had been forwarded to the relevant people on his staff who handle education and immigration. Senator Casey is on the Senate committee on Health, Education, Labor and Pensions so he and his office may be relatively better suited to handling these types of requests. I appreciated the email response, which clearly indicated that someone had actually read my email and was able to understand the two major points.

Maybe this is a lesson for me in that submitting emails through the Senators’ websites is easier than calling them, since each time I called one of Senator Casey’s offices, I had to send automated voice messages.

Update January 29, 2022: Here’s my third update. I was motivated to write this after MIT Professor Gang Chen was cleared of all charges. Here’s his reaction in the Boston Globe. While I’m relieved that he’s in a better place than he was the past year, I still remain concerned that the China Initiative has backfired on the United States, and you can see a more in-depth explanation in this Science article regarding Gang Chen’s case. Thus, I have resumed contacting various political offices and institutions.

• First, after informing Representative Doyle’s office that their website form was not working, I got an email from a staff member at the office, whose background I verified on LinkedIn. I sent a reply summarizing my two main points above (i.e., reforming the China Initiative and providing longer visas). I also submitted the same message again on Representative Doyle’s website, where the form now works. Interesting! Was I really the only one who noticed this website error? I wonder how much traffic his website gets. (Pennsylvania’s 18th Congressional District has a population of roughly 700,000.)

• Next, I sent follow-up emails to both of my US Senators, Bob Casey and Pat Toomey, via their websites. As mentioned earlier, Bob Casey’s office responded to me with an email indicating that someone actually read and understood my message. I sent an email thanking for the correspondence, and I cited the Gang Chen case as a reason for his office to push forward on reforming the China Initiative. Pat Toomey’s office sent a reply which missed the point of my original message (this is different from the phone call above I had with a staff member), so I sent a follow-up email clarifying my original message, but also thanking his office for the correspondence. I like to indicate how much I appreciate getting responses from US Senators.

• I also contacted Pennsylvania Governor Tom Wolf’s office by submitting my standard message on his website (shortened due to character limits). I’m not sure how much power Governor Wolf has over these issues since I think it’s a federal matter. Nonetheless, I figure it is important that the Governor’s office knows about these issues. Furthermore, I assume his office likely has connections with appropriate government agencies who have more relevant power. That brings me to the next point…

• Finally, I just realized that the Department of Justice (DoJ) has a place on its website where we can submit comments. I think the DoJ has the actual authority to reform the China Initiative, so I once again submitted my message there on their website, emphasizing the China Initiative (rather than the visas) to keep the message on-point.

We shall see what happens.

As many readers probably know, I am interested in robotic fabric manipulation. It’s been a key part of my research – see my Google Scholar page for an overview of prior work, or this BAIR Blog post for another summary. In this post, I’d like to discuss two of the three CoRL 2021 papers on fabric manipulation. The two I will discuss propose Visible Connectivity Dynamics (VCD) and FabricFlowNet (FFN), respectively. Both rely on SoftGym simulation, and my blog post here about the installation steps seems to be the unofficial rule book for its installation. Both papers approach fabric manipulation using quasi-static pick-and-place actions.

However, in addition to these “obvious” similarities, there’s also the key issue of representation learning. In this context, I view the term “representation learning” as referring to how a policy should use, process, and reason about observational data of the fabric. For example, if we have an image of the fabric, do we use it directly and propagate it through the robotic learning system? Or do we compress the image to a latent variable? Or do we use a different representation? The VCD and FFN papers utilize different yet elegant approaches for representation learning, both of which can lead to more efficient learning for robotic fabric manipulation. Let’s dive into the papers, shall we?

Visible Connectivity Dynamics

This paper (arXiv) proposes the Visible Connectivity Dynamics (VCD) model for fabric manipulation. This is a model-based approach, and it uses a particle-based representation of the fabric. If the term “particle-based” is confusing, here’s a representative quote from a highly relevant paper:

Our approach focuses on particle-based simulation, which is used widely across science and engineering, e.g., computational fluid dynamics, computer graphics. States are represented as a set of particles, which encode mass, material, movement, etc. within local regions of space. Dynamics are computed on the basis of particles’ interactions within their local neighborhoods.

You can think of particle-based simulation as discretizing items into a set of particles or “atoms” (in simulation, they look like small round spheres). An earlier ICLR 2019 paper by the great Yunzhu Li shows simulation of particles that form liquids and rigid objects. With fabrics, a particle-based representation can mean representing fabric as a grid of particles (i.e., vertices) with bending, shearing, and stiffness constraints among neighboring particles. The VCD paper uses SoftGym for simulation, which is built upon NVIDIA Flex, which uses position-based dynamics.

The VCD paper proposes to tackle fabric smoothing by constructing a dynamics model over the connectivity of the visible portion of the cloth, instead of the entire part (the full “mesh”). The intuition is that the visible portion will include some particles that are connected to each other, but also particles that are not connected to each other and just happen to be placed nearby due to some folds or wrinkles. Understanding this connectivity structure should then be useful for planning smoothing. While this is a simplification of the full mesh prediction problem and seems like it would throw away information, it turns out this is fine for smoothing and in any case is much easier to learn than predicting the full mesh’s dynamics.

Each fabric is represented by particles, which is then converted into a graph consisting of the standard set of nodes (vertices/particles) and edges (connections between particles), and the dynamics model over these is a graph neural network (GNN). Here is an overview of the pipeline with the GNN, which also shows a second GNN used for edge prediction:

The architecture comes from this paper which simulates fluids, and there a chance that this might also be a good representation for fabric in that it can accurately model dynamics.

To further expand upon the advantages of the particle-based representation, consider that the fabric representation used by the graph dynamics model does not encode information about color or texture. Hence, it seems plausible that the particle-based representation is invariant to such features, and domain randomizing over those might not be necessary. The paper also argues that particles capture the inductive bias of the system, because the real world consists of objects composed of atoms that can be modeled by particles. I’m not totally sure if this translates to accurate real world performance given that simulated particles are much bigger than atoms, but it’s an interesting discussion.

Let’s recap the high-level picture. VCD is model-based, so the planning at test time involves running the learned dynamics model to decide on the best actions. A dynamics model is a function $f$ that given $f(s_t,a_t)$ can predict $s_{t+1}$. Here, $s_t$ is not an image or a compressed latent vector, but the particle-based representation from the graph neural network.

The VCD model is trained in simulation using SoftGym. After this, the authors apply the learned dynamics model with a one-step planner (described in Section 3.4) on a single-arm Franka robot, and demonstrate effective fabric smoothing without any additional real world data. The experiments show that VCD outperforms our prior method, VisuoSpatial Foresight (VSF) and two other works from Pieter Abbeel’s lab (covered in our joint blog post).

While VCD does an excellent job at handling fabric smoothing by smoothing out wrinkles (in large part due to the particle-based representation), it does not do fabric unfolding. This follows almost by construction because the method is designed to reason only about the top layer and thus ignores the part underneath, and knowing the occluded parts seems necessary for unfolding.

FabricFlowNet

Now let us consider the second paper, FabricFlowNet (FFN) which uses the idea of optical flow as a representation for goal-conditioned fabric manipulation, for folding fabric based on targets from goal images (or subgoal images). Here is the visualization:

The goal-conditioned setup means they are trying to design a policy \(\pi\) that takes in the current image \(x_t\) and the current sub-goal \(x_i^g\), and produces \(a_t = \pi(x_t, x_i^g)\) so that the fabric as represented in \(x_t\) looks closer to the one represented with \(x_i^g\). They assume access to the subgoal sequence, where the final subgoal image is the ultimate goal.

The paper does not pursue the naive approach where one inputs both the current observation and (sub)goal images and runs it through a standard deep neural network, as done in some prior goal-conditioned work such as our VisuoSpatial Foresight work and my work with Google on Goal-Conditioned Transporter Networks. The paper argues that this makes learning difficult as the deep networks have to reason about the correct action and the interplay between the current and goal observations.

Instead, it proposes a clever solution using optical flow, which is a way of measuring the relative motion of objects in an image. For the purposes of this paper, optical flow should be interpreted as: given an action on a fabric, we will have an image of the fabric before and after the action. For each pixel in the first image that corresponds to the fabric, where will it “move to” in the second image? This is finding the correspondence between two images, which suggests that there is a fundamental relationship between optical flow and dense object neworks.

Optical flow is actually used twice in FFN. First, given the goal and observation image, a flow network predicts a flow image. Second, given pick point(s) on the fabric, the flow image automatically gives us the place point(s).

Both of these offer a number of advantages. First, as an input representation, optical flow can be computed just with depth images (and does not require RGB) and will naturally be invariant to fabric color. All we care about is understanding what happens between two images via their pixel-to-pixel correspondences. Moreover, the labeling for predicting optical flow can be done entirely in simulation, with labels automatically generated in a self-supervised manner. One just has to code a simulation environment to randomly adjust the fabric, and doing so will give us ground truth images of before and after labels. We can then compute optical flow by using the standard endpoint error loss, which will minimize the Euclidean distance of the predicted versus actual correspondence points.

The second, using optical flow to give us placing point(s), has an obvious advantage: it is not necessary for us to design, integrate, and train yet another neural network to predict the placing point(s). In general, predicting a place point can be a challenging problem since we’re regressing to a single pixel, and this can introduce more imprecision. Furthermore, the FFN system decouples the observation-goal relationship and the pick point analysis. Intuitively, his can simplify training, since the neural networks in FFN have “one job” to focus on, instead of two.

There are a few other properties of FabricFlowNet worth mentioning:

• For the picking network, FFN sub-divides the two pick points into separate networks, since the value of one pick point should affect the value of the other pick point. This is the same idea as proposed in this RSS 2020 paper, except instead of “pick-and-place,” it’s “pick-and-pick” here. In FFN, the networks are also fully convolutional networks, and hence do picking implicitly, unlike in that prior work.

• An elegant property of the system is that it can seamlessly alternate between single-arm and bimanual manipulation, simply by checking whether the two picking points are sufficiently close to each other. This simultaneously enforces a safety constraint by reducing the chances that the two arms collide.

• The network is supervised by performing random actions in simulation using SoftGym. In particular, the picking networks have to predict heatmaps. Intuitively, the flow provides information on how to get to the goal, and the picking networks just have to “match heatmaps.”

What is the tradeoff? The system has to assume optical flow will provide a good signal for the placing point. I wonder when this would not hold? The paper also focuses on short-horizon actions (e.g., 1 or 2 actions) starting from flat fabric, but perhaps the method also works for other scenarios.

I really like the videos on the project website – they show a variety of success cases with bimanual manipulation. The experiments show that it’s much better than our prior work on VisuoSpatial Foresight, along with another method that relies on an “FCN-style” approach to fabric manipulation; the idea of this is covered in my prior blog post.

I think this paper will have significant impact and will inspire future work in flow-based manipulation policies.

Concluding Thoughts

Both VCD and FFN show that, with clever representations, we can obtain strong fabric manipulation tasks, outperforming (in some contexts) our prior method VisuoSpatial Foresight, which uses perhaps the most “straightforward” representation of raw images. I am excited to see what other representations might also turn out to be useful going forward.

References:

• Xingyu Lin*, Yufei Wang*, Zixuan Huang, David Held. Learning Visible Connectivity Dynamics for Cloth Smoothing. CoRL 2021.

• Thomas Weng, Sujay Bajracharya, Yufei Wang, Khush Agrawal, David Held. FabricFlowNet: Bimanual Cloth Manipulation with a Flow-based Policy. CoRL 2021.

As the pandemic unfortunately continues throughout the world and is now approaching two years old, the state of affairs has at least given many of us time to adjust to using video conferencing tools. The two that I use the most, by far, are Google Meet and Zoom.

I prefer using Google Meet, but using Zoom is unavoidable since it’s become the standard among my colleagues in academia. Zoom is likely used more widely than Google Meet because of access to China. (Strangely, though, I was recently on a Zoom call with someone I knew in Beijing, who told me he needed a Virtual Private Network (VPN) to use Zoom, so maybe I’m not fully understanding how VPNs work.)

The main reason why I continue using Google Meet is because of the quality of its live transcription. Just before the pandemic started, I remember getting on a virtual call with Google host Andy Zeng for what I call a “pre-interview interview.” (For research scientist internships at Google, typically a host will have already pre-selected an intern in advance.) Being from Google, Andy had naturally set up a Google Meet call, and I saw that there was a “CC” button and clicked on it. Then the live transcription started appearing at the bottom of our call, and you know, it was actually pretty darn good.

When the pandemic started, I don’t think Zoom supported this feature, which is why I asked to have Google Meet video calls for meetings with my involvement. It took a while, but Zoom was able to get live transcription working … but not for Ubuntu systems, until very recently. As of today (November 13, 2021) with Zoom version 5.8.3, I can launch a Zoom room on my Ubuntu 18.04 machine and enable the live transcription, and it works! For reference, I have been repeatedly trying to get live transcription on Ubuntu up until October 2021 without success.

This is a huge relief, but there are still several caveats. The biggest one is that the host must explicitly enable live transcription for participants, who can then choose to turn it on or off on their end. Since I have had to ask Zoom hosts to repeatedly enable live transcription so that I could use it, I wrote up a short document on how to do this, and I put this link near the top of my new academic website.

I don’t quite understand why this feature exists. I can see why it makes sense to have the host enable captioning if it comes from a third party software or a professional captioner, since there could be some security reasons there. But I am not sure why Zoom’s built-in live transcription requires the host to enable. This seems like an unusual hassle.

Two other downsides of the live transcription of Zoom, compared to Google Meet, is that (empirically) I don’t think the transcription quality is that good, and the captions for Zoom will only expand a short width on the screen, whereas with Google there’s more text on the screen. The former seems to be a limitation with software, and Google might have an edge there due to their humongous expertise in AI and NLP, but the latter seems to be an API issue which seems like it should be easy to resolve. Oh well.

I’m happy that Zoom seems to have integrated live transcription support for Ubuntu systems. For now I still prefer Google Meet but it makes the Zoom experience somewhat more usable. Happy Zoom-ing!

This is a regularly updated post, last updated November 12, 2022.

In the past, I have written about some workflow and coding tips, such as improving my development environment with virtualenvwrapper, organizing GitHub repositories, running and saving experiments in Python and understanding (a little) about how docker works.

As I transition to my new postdoc role at CMU as of September 2021, it feels like a good time to recap my current workflow. I am constantly trying to think about how I can be more productive and whether I should learn about this or that feature (the answer is usually “no” but sometimes it is “yes”).

In this blog post, I will discuss different aspects of my current workflow, split into the following sections in this order:

• Conda Environments
• Installing TensorFlow and PyTorch
• CUDA and NVIDIA drivers
• Storage on Shared Machines
• Managing ssh

In the future, I plan to update this post with additional information about my workflow. There are also parts of my prior workflow that I have gotten rid of. Looking back, I’m surprised I managed to get a PhD with some of the sloppy tactics that I employed!

When reading this post, keep in mind that the main operating system I use is Ubuntu 18.04 and that I do essentially all my programming with Python. (I keep telling myself and writing in my New Year Resolution documents that I will get back to coding with C++, but I never do so. My apologies in advance.) At some point, I may upgrade to Ubuntu 20.04, but the vast majority of research code I use these days is still tied to Ubuntu 18.04. I do use a Macbook Pro laptop, but for work contexts, that is mainly for making presentations and possibly writing papers on Overleaf. If I do “research programming” on my laptop, it is done through ssh-ing to an Ubuntu 18.04 machine.

Update 08/06/2022: these days, I still use Ubuntu 18.04 by default, but I now do a fair amount of research work on Ubuntu 20.04 machines. I have not gotten SoftGym working with Ubuntu 20.04, but I can run other software. I also updated this post with a new section on CUDA and NVIDIA drivers and made minor touch-ups to other areas.

Conda Environments

Starting in 2019, I began using conda environments. Previously, I was using virtualenvs coupled with virtualenvwrapper to make handling multiple environments easier, but it turned out to be a huge hassle to manage with various “command not found” errors and warnings. Furthermore, I was running into countless issues with CUDA and TensorFlow incompatibilities, and inspired by this October 2018 Medium article, which amusingly says that if using “pip install” commands for TensorFlow, “There is a probability of 1% that this process will go right for you!”, I switched to conda environments.

Conda environments work in basically the same way as virtualenvs in that they isolate a set of Python packages independent of the system Python. Here, “conda install” plays the role of “pip install”. Not all packages installable with pip are available through conda, but that’s not a huge issue because you can also run normal pip install commands in a conda environment. The process might be delicate, though (see this for a warning) but I can’t remember if I have ever experienced issues with mixing conda and pip packages.

Here’s how I get the process started on new machines:

wget https://repo.anaconda.com/miniconda/Miniconda3-latest-Linux-x86_64.sh
bash Miniconda3-latest-Linux-x86_64.sh

I use miniconda instead of anaconda, but that’s mainly because I prefer something more lightweight to make the process faster and take less disk space. Furthermore, anaconda comes with packages that I would normally want to install myself anyway later (such as numpy) so that I can easily control versions and dependencies.

To be clear, here’s what I do when I run conda envs after that bash command. I accept the license:

I always use the default location (click enter) which is typically /home/<USER>/miniconda3. Then after that I will see:

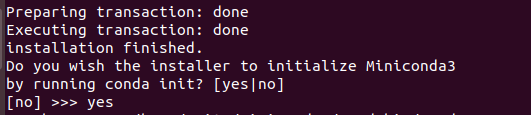
I typically say “yes” so that miniconda automatically adds stuff to my .bashrc file. After this, I can run the “conda” command right away, but I also don’t want the “base” environment to be active right away because I would rather have each new command line window start with a blank non-conda environment. Thus, after closing and re-opening the shell (typically via exiting the machine and ssh-ing again) I do:

conda config --set auto_activate_base false

This information goes into the ~/.condarc file. After refreshing with . ~/.bashrc, conda is all set up for me to use. Here are a few commands that I regularly use:

• conda activate <NAME> and conda deactivate to activate or deactivate the environment. When the environment is activated, use conda install <PACKAGE>.

• conda info --envs to check all my existing conda environments.

• conda list: This will check the installed packages in the current conda environment. This will also conveniently clarify if any packages were installed via pip.

• conda create --name <NAME> python=3.7 -y, to create conda environments with the specified Python version. You can add the “-y” argument to avoid having to explicitly approve the process.

• conda env remove --name <NAME>, to remove conda environments.

We now turn to discussing how conda environments work with TensorFlow and PyTorch.

Installing TensorFlow and PyTorch

Migrating to TensorFlow was the original motivation for me to use conda environments due to running into incompatible CUDA/CuDNN versions with “pip install tensorflow” commands on various machines. You can find a table of TensorFlow packages and their associated CUDA and CuDNN versions here and a popular StackOverflow post here.

As of today, the latest version of TensorFlow is 2.6.0 through pip, but it’s 2.4.1 through conda. A different set of maintainers package the conda TensorFlow version as compared to the one provided through the Python Package Index (PyPI) which is from the official TensorFlow developers, which is why there is some version lag (see this post for some context). Since it’s rare that I absolutely require the latest TensorFlow version, I focus on TensorFlow 2.4.1 here. I run the following commands to quickly start a Python 3.7 conda environment with TensorFlow 2.4.1 installed:

conda create --name tftest python=3.7 -y  &&  conda activate tftest
conda install ipython tensorflow-gpu==2.4.1 -y

Similar Python versions will likely work as well. These days, I use Python 3.6 at a minimum. Also, I just put in ipython since I like running it over the default Python shell. Once I run ipython on the command line, I can try:

import tensorflow as tf
tf.config.list_physical_devices('GPU')
tf.test.is_built_with_cuda()

The tf.test.is_gpu_available() method is deprecated, so use tf.config.list_physical_devices('GPU') instead. Presumably, this should give information that is consistent with what happens when running nvidia-smi on the command line; the first one should list all GPUs and the second one should return True. If not, something went wrong.

This process consistently works for a variety of machines I have access to, and gets TensorFlow working while bundling CUDA internally within the conda environment. This means in general, the conda environment will not have the same CUDA version as the one provided from nvcc --version which is typically the one installed system-wide in /usr/local/. For the commands above, this should install cudatoolkit-10.1.243 in the conda environment. This package is 347.4 MB, and includes CuDNN. Here is another relevant StackOverflow post on this matter.

Finally, wrap things up by removing each created test environment to reduce clutter: conda env remove --name tftest.

Hopefully that helps clarify one way to install TensorFlow in conda environments for shared machines. One day I hope that TensorFlow will be simpler to install. To be clear, it’s simple but could be made a little easier as judged by the community’s reception. (To put things in perspective, remember how hard it was to install CAFFE back in 2014-2015? Heh.) In new “clean” machines where one can easily control which CUDA/CuDNN versions are packaged on a machine on the fly, such as those created from Google Cloud Platform, the pip version could be relatively easy to install.

What about PyTorch? For PyTorch, the process for installing is even easier because I believe that the PyTorch maintainers simultaneously maintain conda and pip packages, because we have the option of selecting either one on the official installation page:

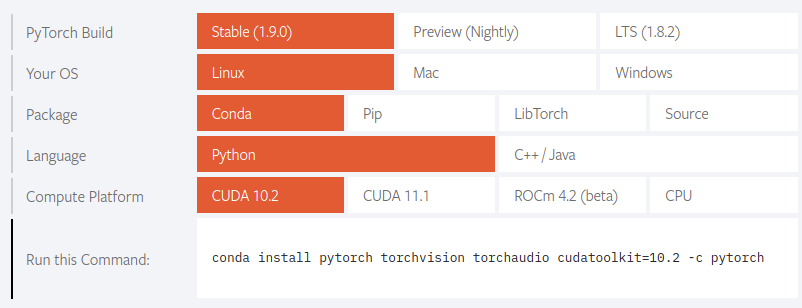
As with my TensorFlow tests, I can test PyTorch installation via:

conda create --name pttest python=3.7 -y  &&  conda activate pttest
conda install ipython pytorch torchvision torchaudio cudatoolkit=10.2 -c pytorch

As of today, this will install PyTorch 1.9.0 along with ipython. Again, ipython is not necessary but I like including it. You can then check if PyTorch is using the GPU(s) as follows:

import torch
torch.cuda.is_available()
torch.cuda.device_count()
torch.cuda.get_device_name(0)

Here is the StackOverflow reference. As with my TensorFlow test, this method of installing PyTorch will detect the GPUs and does not rely on the system’s existing CUDA version because the conda installation will provide it for us. For Pytorch, the cudatoolkit-10.2.89 package (which is 365.1 MB) gets installed, which you can check with cuda list. Once again, this also includes CuDNN.

Clean things up with: conda env remove --name pttest.

CUDA and NVIDIA Drivers

(This subsection was last updated on 08/06/2022.)

Using conda environments, we can bundle CUDA and CuDNN with TensorFlow and PyTorch, which is a huge relief in avoiding headaches with version incompatibilities. However, it is (probably) still necessary to install a system-wide version of CUDA, as well as something called “NVIDIA drivers.” For example, if using a local machine with GPUs (as is common in many AI research labs which have personal machines in addition to servers and clusters), we need NVIDIA drivers to get high resolution displays.

Attempting to install CUDA and NVIDIA drivers in the past has been a nightmare. Fortunately, I think I have found a method that works realiably for me on Ubuntu 18.04 and 20.04 machines.

The first step for me is to install the NVIDIA drivers. I do this first, before installing CUDA. I purge any prior NVIDIA drivers, and then install the recommended drivers using ubuntu-drivers autoinstall and then reboot.

sudo apt-get update
sudo apt-get purge nvidia*
sudo ubuntu-drivers autoinstall
sudo reboot

To check that NVIDIA drivers are installed, I use the widely-used nvidia-smi utility, but there’s also cat /proc/driver/nvidia/version.

To clarify the “autoinstall” part, it will choose the recommended NVIDIA driver to use. You can check which version it will choose:

seita@lambda-dual2:~ $ ubuntu-drivers devices
WARNING:root:_pkg_get_support nvidia-driver-515-server: package has invalid Support PBheader, cannot determine support level
WARNING:root:_pkg_get_support nvidia-driver-515: package has invalid Support PBheader, cannot determine support level
== /sys/devices/pci0000:40/0000:40:01.1/0000:41:00.0 ==
modalias : pci:v000010DEd00002204sv00001458sd0000403Bbc03sc00i00
vendor   : NVIDIA Corporation
driver   : nvidia-driver-515-server - distro non-free
driver   : nvidia-driver-510-server - third-party non-free
driver   : nvidia-driver-515 - distro non-free recommended
driver   : nvidia-driver-510 - third-party non-free
driver   : xserver-xorg-video-nouveau - distro free builtin

seita@lambda-dual2:~ $

In the example above, I’m on an Ubuntu 20.04 system with RTX 3090 GPUs, and thus the “recommended” NVIDIA driver is 515.

The references that I rely on for this process include this, this, this, and this. This post from the NVIDIA forums was also helpful, though the poster from NVIDIA requests us to use published instructions from NVIDIA. The issue is that when I have done this, I have run into numerous errors with displays not working and needing to use “tty” mode to access my machine.

Then after this, I install CUDA by using the runfile, not the debian file. For that, I go to this page from NVIDIA to download the appropriate CUDA toolkit for my system. The runfile will be named something like this: cuda_11.3.0_465.19.01_linux.run.

I follow the installation instructions for the runfile, but when I do the installation, I do not install the drivers! I just install the toolkit, like this:

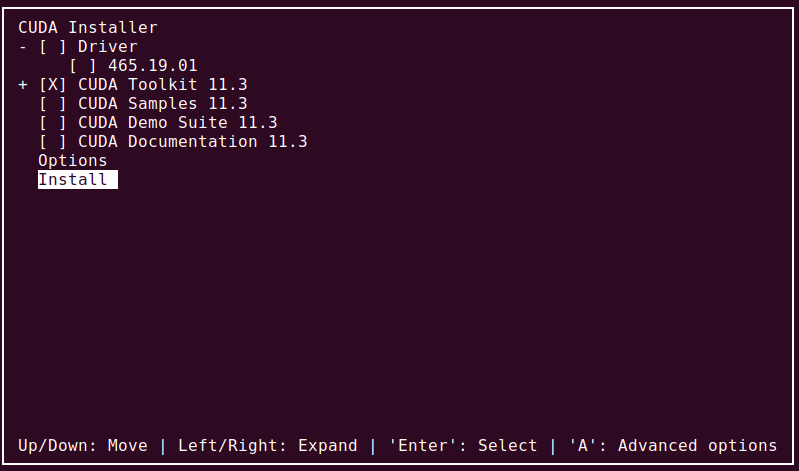
Above, I am only selecting the CUDA Toolkit, since I installed the drivers, and the other parts are not relevant.

If the installation works (a reboot might be needed), the CUDA toolkit should appear in /usr/local:

seita@takeshi:~$ ls -lh /usr/local/
total 40K
drwxr-xr-x  2 root root 4.0K Jul  5 14:34 bin
lrwxrwxrwx  1 root root   21 Aug  4 10:46 cuda -> /usr/local/cuda-11.3/
drwxr-xr-x 17 root root 4.0K Mar  6 19:04 cuda-11.2
drwxr-xr-x 15 root root 4.0K Aug  4 10:46 cuda-11.3
drwxr-xr-x  2 root root 4.0K Sep 15  2021 etc
drwxr-xr-x  2 root root 4.0K Sep 15  2021 games
drwxr-xr-x  2 root root 4.0K Sep 15  2021 include
drwxr-xr-x  3 root root 4.0K Mar  6 18:31 lib
lrwxrwxrwx  1 root root    9 Mar  6 18:30 man -> share/man
drwxr-xr-x  2 root root 4.0K Sep 15  2021 sbin
drwxr-xr-x  6 root root 4.0K Sep 15  2021 share
drwxr-xr-x  2 root root 4.0K Sep 15  2021 src
seita@takeshi:~$

For example, here we see that the default CUDA toolkit is 11.3 because that’s where the cuda “symlink” is pointing to, but I could have easily set it to be 11.2. We can check with nvcc --version. If that’s not working, you might need to check your ~/.bashrc for something like this:

export CUDA_HOME=/usr/local/cuda
export PATH=${CUDA_HOME}/bin:${PATH}
export LD_LIBRARY_PATH=${CUDA_HOME}/lib64:$LD_LIBRARY_PATH

I recognize that these are not exactly the published NVIDIA instructions and that I’m probably missing something here, but this has been a simple way to get things working.

Another post from StackOverflow that helped me understand things was this one which clarifies that we might get different CUDA versions from nvcc and nvidia-smi after this process. I have had this happen on many of my machines without problems.

Managing Storage on Shared Machines

In academic research labs, students often share machines. It thus helps to have a scalable, efficient, and manageable way to store data. Here’s how I typically do this for machines that I administer, where I am a “sudo” user and grant access to the machine to other lab members who may or may not be sudo (for example, I rarely make new undergrad researchers sudo unless there’s a good reason). I assume that the machine is equipped with a separate SSD and HDD. The SSD is typically where users store their local data, and because it’s an SSD rather than an HDD, reading and writing data is faster. The HDD is mainly for storing larger datasets, and typically has much more storage than the SSD.

For a clean machine, one of the most basic first steps is to make sure that the SSD and HDD are mounted upon startup, and accessible to all users. Usually, the SSD is automatically mounted, but the HDD might not be. I can mount these drives automatically by editing the /etc/fstab file, or by using the “disks” program, which will end up editing /etc/fstab for me. I suggest following the top answer to this AskUbuntu question. My convention is to mount the HDD under a directory named /data.

To inspect file systems, I use df -h, where the -h argument makes the sizes human-readable. Here’s an example of a subset of the output when I run df -h:

Filesystem      Size  Used Avail Use% Mounted on
/dev/nvme0n1p1  1.9T  1.2T  598G  67% /
/dev/sdb1        13T  571G   12T   5% /data

According to the above, the SSD has 1.9T of total space (of which 67 percent is used), and the HDD has 13T of total space. The output of df -h includes a bunch of other lines with information that I’m not sure how to interpret; I am guessing those correspond to other minor “drives” that are needed for Ubuntu systems to function. I only use df -h to look at the SSD and HDD, to make sure they are actually there, and to check disk space.

Incidentally, another way I check disk space is by using du -sh <directory>, which will list space recursively stored under <directory>. Depending on user privileges, the command might result in a lot of distracting “permission denied” warnings, in which case I add 2> /dev/null at the end of the command to suppress those messages. I recommend reading this article for more information and useful tips on managing disk space.

After mounting the HDD, it is typically under control of root for both the user and the group, which you can check with ls -h /. This is problematic if I want any user to be able to read and write to this directory. To resolve this, I usually follow the top answer to this AskUbuntu question. I typically make a new group called datausers, and then add all users to the group. I then change the ownership of the shared folder, /data. Lastly, I choose this option:

sudo chmod -R 1775 /data

According to the AskUbuntu question, this means that all users in datausers can add to /data, and can read but not write to each others files. Furthermore, only owners of files can delete them, and users outside of datausers will be able to see the files but not change them.

From these steps, running ls -lh / shows:

user@machine:~$ ls -lh /
drwxrwxr-t    6 root datausers 4.0K Sep 17 21:43 data

As with df -h, I am only showing part of the output of the above command, just the line that lists data. This shows that it is correctly under the group “datausers.”

Finally, I reboot the machine, and then now users who are in the datausers group should be able to read and write to the /data without sudo access. Furthermore, unless sudo privileges are involved, users cannot modify data from other users in /data.

Managing ssh

I use many machines for work, so I need to seamlessly connect to them from any one machine (including from a personal laptop). I use ssh: ssh daniel@<ID>, where daniel is a hypothetical username for me on a machine, and <ID> should be replaced with some corresponding machine ID number, which often looks something like 123.456.7.890 with a few numbers spaced out with periods.

When I get started with a new machine, a common question I have for myself is: what is the ID for ssh? I often use ifconfig to find the ID, though I admit that sometimes it’s not clear from this command. If you’re trying to connect to a machine as part of a research lab, typically the lab will have already set some kind of address to conect with SSH. If this is a new machine, don’t forget that it needs to have the ssh server on to accept connections (see this AskUbuntu post).

Sometimes machines will restrict ssh access to particular ports, which means I connect with ssh -p PORTNUM daniel@<ID>. When a port number is necessary for ssh connectivity, I have been able to find the right port by running this command (source):

sudo grep Port /etc/ssh/sshd_config

I also highly recommend using ssh keys. By sharing keys among machines, this means one can avoid typing in passwords. This is an enormous benefit for me since I might need to connect with as many as 10 different lab servers, and I use different login passwords for each machine. For more information, I recommend checking a source like this guide. But to summarize, here’s what I do. Assuming I have a key from running ssh-keygen, then on my current machine, I run a command like this:

ssh-copy-id -i ~/.ssh/id_rsa daniel@<IP>

This is the same as a standard normal ssh command, except it has ssh-copy-id and a reference to the (public) key that I am trying to copy to the other machine.

Assuming that command works, I should then be able to run ssh daniel@<IP> from my current machine to the one specified with the <IP>, without typing in a password. Amazingly, for something that I rely a lot on for my ongoing day-to-day work convenience, I didn’t even know about this feature until halfway through my PhD.

Conclusion and Outlook

Using conda environments has been a huge help for my research workflow, and makes it easy to manage multiple Python projects. I have also been fortunate to get a better sense for how to effectively manage a finite amount of disk space among multiple users.

Some stuff that I also use in my current workflow, and would like to write more about in the future, include VSCode, vim, more on managing ssh and internet connectivity, and Docker. I also would like to understand how packages work for C++, to see how the process contrasts with Python packages.