I have now completed the first class sessions for all the courses I’m taking this semester.

And I’m relieved.

I’ve always found the first session to be the most awkward of all class sessions. The reason is that, due to my class accommodations, there are typically two sign language interpreters (or sometimes in the past, captioners/CART-providers) who show up to the class with me. They sit near the lecturer, so they’re impossible to miss.

Consequently, when it’s the first day of class, I sometimes get paranoid and wonder if students are constantly thinking about the extra people in the room. Or, worse, what if they’re repeatedly looking at me? After all, other students might be curious about who on earth might actually need such accommodations. When I think about this, my face feels a bit hotter and I sometimes wish I could hide and blend in like a “normal” student, for once.

That’s not to say I never want people to think about me. For instance, if I knew students were thinking something similar to: wow, that guy over there who needs sign language accommodations must be reasonably good at this material or possess ability to work extremely hard, given his inherent disadvantages, well then perhaps I shouldn’t feel so awkward.

Of course, the point is that I don’t know what other students think of me, so I default to a more pessimistic view.

The worst part about these first sessions is when the interpreting integration does not go seamlessly. When this happens, it’s usually because someone arrived late to class. One of the most awkward first class sessions for me occurred back in my sophomore year of college. I was taking intermediate microeconomics with about 50 students in it. The school administration gave my interpreters the wrong room number, and I had failed to notify them after only recently finding out myself.

This meant that the interpreters showed up five minutes late to the first class, after everyone got seated. They caused a brief interruption, with one interpreter telling me what happened, and the other one introducing themselves to the professor.

Yes, that was pretty awkward. My face was a little red and I kept my eyes firmly focused on the board, hoping that the other 50 students wouldn’t look at me for more than few seconds.

Don’t misunderstand what I’m saying – there are times when I really like the attention. For instance, as I’ve stated a few times in this blog, I enjoy giving talks (e.g., project presentations), so I like the attention in those cases.

I just don’t like being highly visible when it’s the first day and a bunch of students who don’t know me have to suddenly get used to the interpreting services in the class.

In addition to bearing the initial awkwardness over the accommodations, I have a few other first-day concerns. One is that I know I have to arrive early to classes to make sure I can get a seat in the front row of the class, preferably at one of its “ends” since that results in the optimal positioning for me and the sign language interpreters (and probably for the other students; I don’t want to know how annoyed they’d be if the interpreters sat in the center of the room).

Due to the enrollment surge in graduate-level EECS courses, if I don’t manage to quickly secure one of those coveted front-row seats, then I probably have sit or stand near the front corner. For me, it’s better to stand near the front than sit in the back, but fortunately I’ve never had to weigh that tradeoff. In all my classes this semester – in fact, in every class I’ve had in recent memory – I’ve always been able to secure a front-row seat, but it’s still a concern for me.

Fortunately, with the first class sessions behind me, things should improve. From past experience, after about four weeks, everyone seems to get used to the interpreters, and a few wonderful students and professors start socializing with them (and me!).

Furthermore, after the first class, it becomes clearer to me and the interpreters how to best position ourselves for maximum benefit. I’ve had to suggest changing our seats a few times.

All right, I guess what I really want to say is that I’m looking forward to my next few classes.

Two and a half years ago, I wrote a post about programming in Python. One of my tips was to use the Python shell, so that one can quickly test simple commands before integrating them in a more complicated project.

Fast forward until now, and my Python habits have changed substantially. One notable change I have made is to use IPython instead of the Python shell. For my usage purposes, the IPython shell has been a strictly superior version of the standard one due to the following:

• It includes TAB completion for functions. For instance, suppose I’m importing the numpy library, and I want to create an array variable, which means I need the array function. I start the IPython shell (by typing ipython on the command line), import the numpy library, and when I press the TAB key after a = np.arr, I get the output:

In [1]: import numpy as np

In [2]: a = np.arr
np.array         np.array2string  np.array_equal   np.array_equiv   np.array_repr    np.array_split     np.array_str     

IPython is smart enough to tell me which methods I might be interested in using! It’s a really nice feature, and I’ve found that it also works when one tries to autocomplete function parameters. In the standard Python shell, typing TAB just means … creating extra TABs.

• It makes it easier to fix for loops, which is handy because it’s really easy to make a mistake with loops. Consider the trivial example below:

In [2]: for i in range(4):
   ...:     print "hi""
   ...:     
    File "<ipython-input-2-f57d06c46d12>", line 2
            print "hi""
                     ^
    SyntaxError: EOL while scanning string literal

In IPython, to fix the loop, I just need to press the UP key and it will load both lines of the for loop. In the standard shell, the UP key would only return print "hi"", forcing the user to essentially retype the loop.

• It remembers commands from previous sessions, so I can exit an IPython session, do other stuff, then restart IPython, press the UP key, and it will give me the commands I used in my last session.

These three are the extra IPython features that have been most useful for my work.

I frequently use Python for work because it is a simple language that has lots of robust math, machine learning, and data analysis libraries. My favorite Python library is matplotlib, which is used for forming high-quality plots.

A few months ago, my workflow for using matplotlib was to write a script that first gets the data into a matplotlib plot, and then saves it (using the savefig(...) function). When I need to make lots of figures, however, it gets cumbersome to manage them, and I often have to keep multiple images open so I can spot-check their changes when I re-run my script (e.g., if I modified the font size of the text).

Fortunately, I discovered Jupyter Notebooks. These are brower-based platforms that make managing matplotlib-based images far easier by keeping information unified in one screen.

To start a notebook session, I type in ipython notebook on the command line, which opens up a web browser (for me, it’s Firefox). I then click New -> Python 2 to start the session. For a basic plot, I can start by importing the library: import matplotlib.pyplot as plt, but then — crucially — I use the %matplotlib inline command. The reason for using that is so that when I write code to plot, and then execute it with a simple SHIFT-ENTER, the image will appear directly under that code cell. Here’s a simple example:

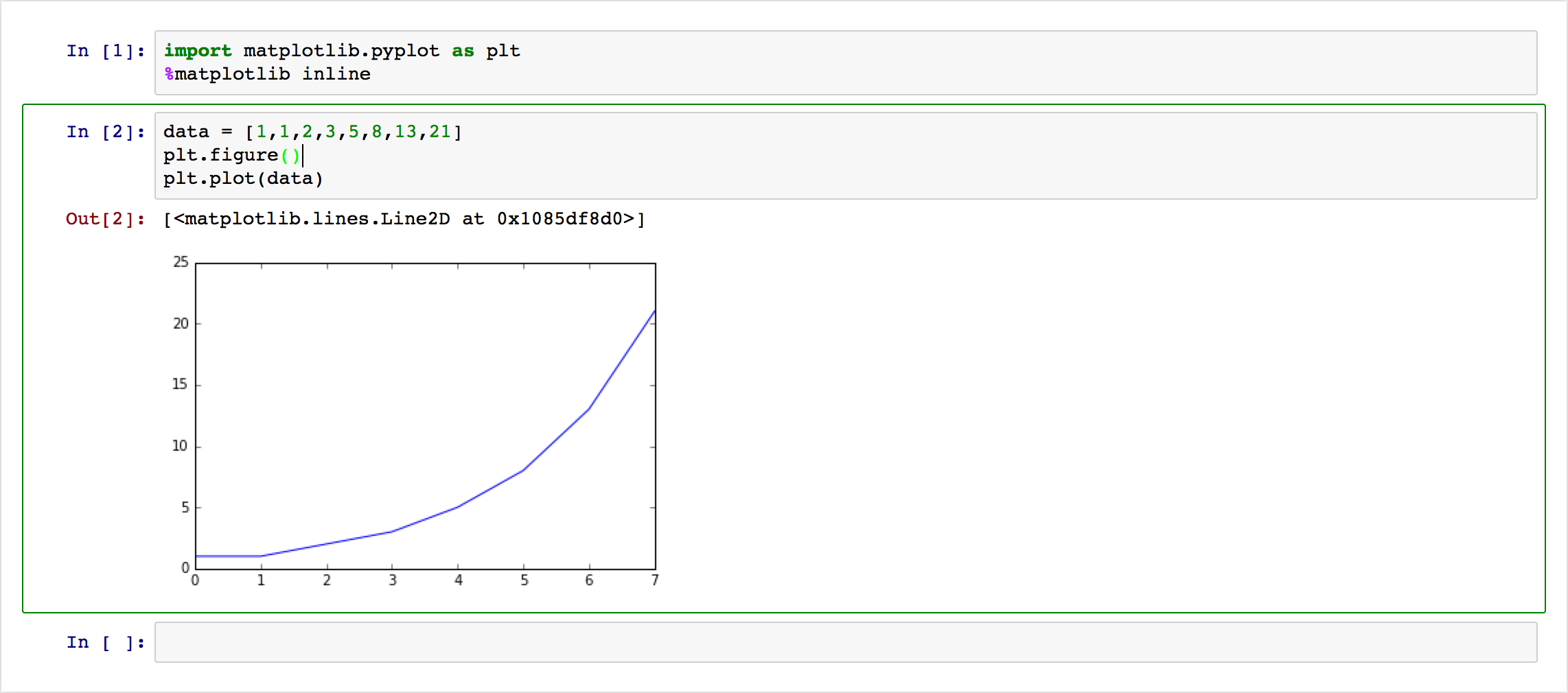
This is nice, but what if I want to change some plot setting? If these images are going to be in an academic paper, they better have labels and legends, among other things. With these notebooks, one can modify the text in a cell and regenerate the image; here’s an example with some common commands I use for my plots:

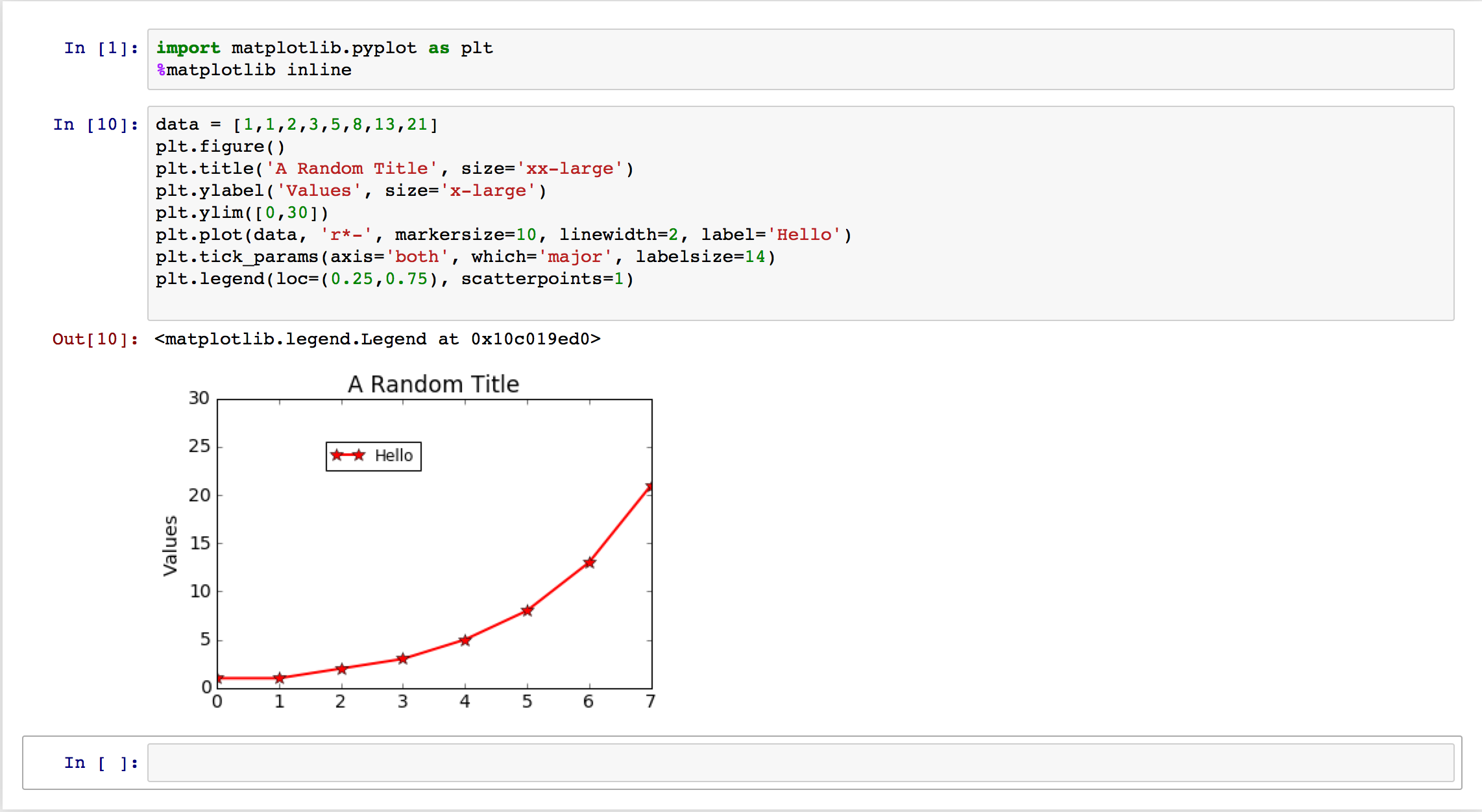
This example doesn’t quite show the benefit enough, but once projects get more complicated, notebooks are a valuable tool to keep data organized. Moreover, one can save a notebook session so that the next time it gets opened again, its plots remain visible on the webpage.

For those of you who use Python, I encourage you to check out IPython and Jupyter. They add on to what is already an awesome general-purpose programming language.

This link on Berkeley “By the Numbers” states that 73 percent of undergraduate classes have fewer than 30 students.

That statistic is (painfully) amusing for me to think about, because I’ve only taken graduate courses here, and none has had fewer than 30 students. In my class reviews, I frequently discuss enrollment, so let’s recap:

• CS 280, Computer Vision was overenrolled and had people sitting on the floor in Soda 306. The course staff had to force undergraduates to drop the course.

• CS 281A, Statistical Learning Theory had one of the largest (if not the largest) rooms in Cory Hall, and we still had people sitting on the floor during the first few lectures. This is despite how CS 281A was offered the semester before I took it. Most graduate courses never get offered in consecutive semesters.

• CS 287, Advanced Robotics. This is the only class where I can get a precise picture of enrollment in previous years, since the CS 287 course websites list the final project presentation schedule and I can count the students. (The Fall 2015 edition is on Piazza, not the official website.) The Fall 2009, 2011, 2012, 2013, and 2015 classes had the following respective number of students give project presentations: 19, 36, 15, 48, and 58.

• CS 288, Natural Language Processing was overenrolled at the start; the professor said in his introductory email that “Since there are 80+ of you interested in what is normally a 20-person class, I wanted to be clear about how we’re planning to handle enrollment […].” Even with students eventually dropping, I am almost positive we had well over 30 students, possibly over 40 remaining at the end of the semester.

• CS 294: Deep Reinforcement Learning was overenrolled and the staff moved the room and offered two lecture times. In theory, deep reinforcement learning is just one “small sub-research area” of Artificial Intelligence, but in reality, it’s probably the most popular of those areas.

• EE 227BT: Convex Optimization was also quite crowded, though I don’t know if enrollment was that much greater than in previous years, but I don’t think having 50-60 students should be the norm in a graduate-level course.

It should be clear that this is due to the growing popularity of computer science as a major and a graduate degree (this page provides some hard statistics on Berkeley’s CS enrollment). The result is that Berkeley and similar schools have had to drastically expand the size of faculty and lecturers, but I worry about what will happen long-term if enrollment abruptly declines, say in five years. I wasn’t old enough to understand the dot-com bust, but I think I may need to go and read some of the literature on that era to have a better idea if history is repeating itself.

As the year 2015 wraps up, I’ve been reviewing my New Year’s Resolution document. Yes, I do keep one; it’s on my laptop’s home screen so I see it every time I start my computer. No, I unfortunately did not manage to accomplish anything remotely close to my original goals.

I did, however, read more books this year than I did in previous years. I was a committed gamer back in high school and college and I’m trying to transition from playing games to reading books in my free time (in addition to blogging, of course).

In this post, I would like to briefly share some thoughts on three of my favorite books I read this year: Guns, Germs, and Steel, The Ideas that Conquered the World, and (yes, sorry) The God Delusion.

Guns, Germs, and Steel

Guns, Germs, and Steel: The Fates of Human Societies, by Jared Diamond, is a 1998 Pulitzer Prize- Winning (General Nonfiction) book about, essentially, how human societies came to be the way they are today. It aims to answer the question: Why did Eurasians conquer, displace, or decimate Native Americans, Australians, and Africans, instead of the reverse?

The white supremacists, of course, would say it’s because Caucasians are superior to other races, but Diamond completely eviscerates that kind of thinking by presenting strong geographic and environmental factors that led to Eurasia’s early dominance. Upon the age of exploration, it was Europe which contained the most technologically advanced and most powerful countries in the world. (Interestingly enough, this was not always the case in the world; Australia and China had their turns as being the most advanced countries in the world.) That European explorers had guns were not the main reason why they conquered the Americas, though: it was because they were immune to diseases such as smallpox that decimated the native populations.

I learned a lot from this book. Seriously, a lot. The book was full of seemingly unimportant factors that turned out to have a major impact on the world today, such as the north-south shape of the Americas versus the east-west nature of Eurasia. While I was reading the book, I kept repeating to myself: wow, that argument should have been obvious in hindsight, an indication that the book was effectively supporting its hypotheses. I felt a little uncomfortable when Diamond had to add several disclaimers in the book that it was not going to be “a racist treatise” but unfortunately that text is probably still necessary in today’s world.

A negative effect of reading this book was that, since it deals with the growth of human civilizations, it made me want to play some Civilization IV, but never mind. This was a great book.

The Ideas that Conquered the World

The Ideas That Conquered The World: Peace, Democracy, and Free Markets in the Twenty-first Century, by Michael Mandelbaum is a 2002 book that reviews the state of Western values at the start of the 21st century. If one compares life today to what it was like during the Cold War and earlier, some of the most remarkable trends are that countries heavily prefer peace as the basis of foreign policy, democracy as the basis of political life, and free markets as the basis of economic growth. Mandelbaum explains how these trends occurred by providing an overview of how countries previously conducted internal and foreign affairs from 1800 to the present. He particularly analyzes the impact of World War I, World War II, and the Cold War on liberal values.

There are many interesting themes repeated in this book. One is that Germany and Japan serve as the ultimate examples of how previously backward countries can catch up to the world leaders by adopting liberal policies. Another is that there are three “dangerous” regions in the world that could threaten peace, democracy, and free markets: the Middle East, Russia, and China, since those countries wield considerable power but have not completely adopted liberal principles. (In 2015, with all the terrorism, oil, and migrant crises in the Middle East, along with America’s diplomatic tensions with Russia and China, I can say that Mandelbaum’s assessment was really spot on!) A third theme is that much of the world has actually become less peaceful after the Cold War, a consequence of how the core countries now have fewer incentives to protect those countries on the periphery.

Of the three books here, this one is probably the least well-known, but I still tremendously enjoyed reading it. I now have a better understanding about why there is so much debate over government size in American politics. The role of the government in a free market society should be to let the market function normally, except that it should provide a social safety net and other services to protect the worst effects of the market. How much and to what extent those services should be provided is at the heart of the liberal versus conservative debate. As a side note: I find it really interesting how “liberal” is related to the free market, yet the stereotype in today’s politics is that conservatives, not “liberals” as in “Democrats”, are the biggest free market supporters. That’s vastly oversimplifying, but it’s interesting how this terminology came to be.

Oh, I should mention that this book also made me want to play Civilization IV. Perhaps I should stop reading foreign policy books? That brings me to the third book …

The God Delusion

The God Delusion, by Richard Dawkins, is a 2006 book arguing that it is exceedingly unlikely for there to be a God, and that there are many inconsistencies, problems, and harmful effects of religion. This is easily the most controversial of the three books I’ve listed here, for obvious reasons; a reviewer said: “Bible-thumpers doubtless will declare they’ve found their Satan incarnate”.

Dawkins is a well-known evolutionary biologist but is even more well-known for being the world’s prominent atheist. In The God Delusion, Dawkins presents a spectrum of seven different levels of beliefs in God, starting from: (1) Strong theist. 100 per cent probability of God. In the words of C.G. Jung, ‘I do not believe, I know’ to (7) Strong atheist. ‘I know there is no God, with the same conviction as Jung “knows” there is one.’.

Both Dawkins and I classify ourselves as “6” on his scale: Very low probability, but short of zero. De facto atheist. ‘I cannot know for certain but I think God is very improbable, and I live my life on the assumption that he is not there’. I also agree with him that, due to the nature of how atheists think, it would be difficult to find people who honestly identify as falling in category 7, despite how it’s the polar opposite of “1” in his scale, which is very populated.

This book goes over the common arguments that people claim for the existence of God, with Dawkins systematically pointing out numerous fallacies. He also argues that much of what people claim about God (e.g., “how can anyone but God produce all these species today?”) can really be attributed to a one-time event, plus the cumulative nature of evolution. In addition, Dawkins discusses the many perils of religion, about how it leads to war, terrorism, discrimination, and other destructive practices. For an obvious example, look at how many Catholics have a negative and inflexible view of homosexuals and homosexuality. Or for something even worse, look at ISIS.

The God Delusion ended up mostly reinforcing what I had already known, and expresses arguments in a cleaner way than I could have ever managed. This brings up the question: why did I already identify as being in category 6 on Dawkins’ scale? The reason is simple: I have never personally experienced any event in my life that would remotely indicate the presence of God. If the day were to come when I do see a God, then … I’ll start believing in God, with the defense that, earlier, I was simply thinking critically and making a conclusion based on sound evidence. After all, I’m a “6”, not a “7”.

Dawkins, thank you for writing this book.

In computer science graduate-level courses at Berkeley, it is typical to have final projects instead of final exams. There are two ways in which these projects are disseminated among the students:

• Class Presentations. These are when students prepare a five to ten minute talk to the class, using slides and other demos to state the project’s main accomplishments. Due to explosions in class enrollment (see my class reviews here for examples), time limits are strictly enforced, so presentations must be precisely timed and polished.

• Poster Sessions. These are when students bring a poster describing their work. Usually, students create posters by stuffing lots of images and text in a power point slide (or other software). Then they print using their lab’s poster printer.

I’ve experienced both scenarios at Berkeley, and based on those I would strongly state the following to instructors: class presentations are better than poster sessions, and should be the method of choice for dissemination of final projects.

First, a class presentation means students practice a useful skill, one that they will likely need for their future careers. This is especially true for academic careers, and students taking graduate-level courses are far more likely to want academic careers than the average undergrad. For me, presentations are also a way that I can channel my humor, which isn’t immediately apparent to other students. A second, less important reason, is that in an age of exploding enrollment in graduate courses, it’s nice to be able to finally learn people’s names when they give class presentations.

One can, of course, learn names and project accomplishments in poster sessions, but this requires more effort and is challenging for people like me. I have lots of difficulty navigating my way through loud, noisy poster sessions filled with accents. I either resort to reading people’s posters (and not understanding much of it anyway due to time constraints) or going through the awkwardness of having a sign language interpreter with me (and having that interpreter struggling through accents and technical terms).

Poster sessions have other downsides that apply broadly, and not just to deaf students. For instance, poster sessions allow students to hide. What happens if students don’t manage to do much for their final projects? As I’ve seen happen in my classes, these students go to the corner of the room to avoid the spotlight. Presentations avoid this issue, unless students are willing to go as far as to even skip their presentation time. Some students who are nervous about public speaking might also want to hide. To most of them, I would respond: good luck convincing your future bosses to have you not do any presenting.

If class presentations force students to produce something that is worth presenting and force them to encounter their fears, then that’s probably sufficient reason alone to use them!

There are other downsides to having poster sessions. They cost more, creating a chasm between students who have access to fancy poster printers and those who don’t; the latter may have to resort to printing out ten pages of work and pasting them together in a poster. Furthermore, the posters that get printed are unlike to be used again, in the exact form. True, many conferences have poster sessions due to scalability issues, but class projects are not generally up to par with research projects, so students would have to re-print posters anyway. And that’s assuming that students are using class projects as the basis for future research, which isn’t always the case.

Class presentations are also superior to poster sessions in that they require less physical room. The presentations can be delivered in the same lecture room, while poster sessions force the course staff to go through the trouble of finding and reserving a large room (or hallway, as is the case for Berkeley).

Furthermore, the one “benefit” of poster sessions, scalability, does not stand up to a rigorous analysis. (If there are other benefits, please let me know because I can’t think of any.)

First, if the class size is so large that it approaches the enrollment of a popular academic conference, then would the course staff really have time to read the final reports? Remember, neither presentations nor poster sessions enable people to fully understand a project; for this, one has to read papers.

Second, with five minutes per presentation, the process goes by quickly, and it is also easier for the course staff to track progress. Also, with a large class, it is likely that students would be encouraged to form groups, drastically reducing the quantity of presentations. If there’s too many presentations for one class, the course staff should divide the class into groups.

Finally, scheduling presentations is not generally a problem even with many groups. Here’s a simple procedure: have a random draw to see who goes next. If the class requires a fixed schedule, then busy instructors should have their TAs form the order of presentations.

Unfortunately, the classes I’m taking next semester have historically used poster sessions rather than verbal presentations, but perhaps I could convince them to change their minds?

The third class I took this semester was Convex Optimization (EE 227BT), which was also my first time wading into electrical engineering. There are three convex optimization courses at Berkeley: EE 227A, EE 227B, and EE 227C. (Note: I say 227BT in this title because the course had a “T” for “Temporary,” but that should go away soon.) I did not take the first course, EE 227A, and I think that may have been a reason for my struggles in this class.

To do well in EE 227B, I think one needs to be highly skilled in the following two areas: linear algebra and problem solving. If a student lacks one or both of these skills, he or she is in serious trouble. For a linear algebra concept, consider this problem: \(\max_{\{x : \|x\|_2=1\}} x^TAx\) for symmetric \(A\). We encountered this at the start of the semester and would see it over and over again. The professor, Laurent El Ghaoui, said: “If you didn’t immediately know that the answer to this was the maximum eigenvalue of \(A\), or \(\lambda_{\max}(A)\), then run away to EE 227A. This is all linear algebra.” I did know that, in fact, but the class material was nonetheless very difficult for me to understand.

We had five problem sets, and I think they were among the hardest ones I’ve ever had, and also more challenging than those from CS 281A. After spending 30 to 40 hours on the first few homeworks, I realized I needed to seriously start reaching out to other students to get more than two-thirds of the homework done correctly, and I did do that this semester.

Each problem set contained three to five questions, each of which had some number of sub-problems. Their difficulty varied considerably, with some parts following directly from the definition of Cauchy-Schwarz, \(x^Ty \le \|x\|_2\|y\|_2\) (not Cauchy-Schwartz … I don’t know why people keep misspelling that), and others requiring some ridiculously complicated insights. The hardest one was to prove Theorem 4 and Corollary 3 from Laurent’s paper Sparse Learning via Boolean Relaxations. Yes, we had to do that, and no, we were not given this paper reference and had to start some of that from scratch. I found out about this paper from another student. Also, the paper was published in 2015, so it must have been difficult since no one else did this until now. Setting the boolean relaxation problem aside, the homework questions were challenging but doable with some problem solving insights (one might need help for these, though), and they were brutally educational.

In terms of homework logistics, we had a paid grader who graded the homeworks, which is different from the previous iteration of the course (Fall 2014) when students had to self-grade their submissions. Note that Laurent’s EE 227BT website is (currently) incorrect; I think he recycles the same links for his classes, so some of it is out of date for the Fall 2015 edition. Our grader was surprisingly generous with points but did not offer detailed feedback and also took three or four weeks before providing grades. In part, this was because of the large class size. We had perhaps eighty students at the start before setting to fifty or sixty.

One of the “less-awesome” aspects of this class, in my opinion, was that we barely followed the projected outline. We were supposed to get five homework assignments, released every other Thursday, which meant we would get two weeks to do each assignment. However, because the lectures quickly fell behind from the outline, Laurent delayed the second homework by a week, which caused a few more subsequent delays for other assignments. This meant that homeworks eventually spilled over into time that was originally designated for us to do final project work. I think it would be best to design homeworks conservatively so that even if the lectures get delayed, there’s no need to put off the homework due dates.

We had a midterm, but that was also delayed, by a week. It was in-class for 80 minutes, open note (but not open laptop or Internet). It had three questions, each with multiple parts, and was out of 40 points total. Judging from the distribution of scores, I think most students got somewhere between 15 and 30 points. It was definitely a challenging midterm, but in retrospect, I thought it was fair, and was of higher quality compared to the CS 280 midterm.

The third part of our grade was based on the final project. We started final project discussions really early, in September! Almost from the beginning, Laurent designed lectures so that we would cover standard concepts (e.g., Lagrange duality) for 75 minutes, and then the last 5 minutes would be an open discussion of final project ideas. Despite the early focus of final projects in the lectures, in reality we didn’t have that much time to work on them due to the homeworks and midterm getting delayed and cutting into project time. I think the course staff should address this in future iterations of the course.

I worked in a group of four in my final project, where we investigated various properties of neural networks. We read a lot of research papers (the “literature review” that Laurent kept saying in lecture) and ran experiments using CAFFE and CVX. We wrote this up in a forty-page final project report. Going through and editing that at the end was a lot of work! A quick warning to future students: the project report date was set before RRR week, which I think is unusual for most graduate courses, which allow students to work on reports through mid-December.

In addition to a report, we had project presentations, which I was happy about since it’s fun to give talks. Not all students would agree with me. During the presentations, my sign language interpreters would comment on some of the students who appeared to be really nervous. To make matters worse, Laurent brought a hand-held microphone to the class, and about half of the students actually held the microphone when they were talking. No, I’m serious! And it’s not like we were on stage at Broadway — we were in a normal-sized classroom! I don’t like holding a microphone because it would make it completely obvious to the rest of the class that I was nervous about public speaking! I think Laurent had good intentions about bringing the microphone, but to future students, please don’t use microphones when talking.

When it was my turn to present, I put the microphone away after someone handed it to me (sorry, not using it!) and immediately started off with a planned joke. I told the class to pretend that Laurent and I were “trapped in a world that represents the loss function of the neural network.” (Don’t ask why!) I continued the story: I led Laurent to a local minimum, but he got angry and wanted the global minimum. I calmly responded that local minima are just as good as the global minimum in neural networks. I added a little acting and tried to cleverly alter my tone of voice. The class roared in laughter, and I think that was probably the most successful joke I have ever pulled off in a class presentation.

To wrap up my thoughts on EE 227B, I think it is similar to most classes I’ve taken in the sense that it is challenging, but very educational. I now feel like I have a much better understanding of concepts in linear algebra, especially those about norms, eigenvectors, and matrix decomposition. Many students who take this course do research in Artificial Intelligence fields, and EE 227B enables students to read AI research papers without getting bogged down by the notation and definitions. This was a huge problem for me when I first started to read machine learning papers a few years ago. I couldn’t even consistently remember what \(\|x\|\) meant! Thanks to EE 227B, and some of my own independent linear algebra studying, I’ve cleared a lot of that initial “notation hurdle”.

Finally, to future students who are considering this class, the best advice I have is to make sure that your linear algebra skills are sharp. In particular, be sure you know about matrix norms, eigenvectors, and other forms of matrix decomposition (e.g., Singular Value Decomposition).

If you’re weak in those areas, then in the words of Laurent, “run away to EE 227A.”

I took Advanced Robotics (CS 287) last semester, which is the graduate level class that Pieter Abbeel teaches at Berkeley. You can view the course website here. Robotics is a vast, highly interdisciplinary field, so to restrict the focus, CS 287 is about the math and algorithms of robot systems. No, we didn’t see giant, science-fiction style robots battle each other, but we did observe a research robot tie knots (alas, through videos, not in real time).

Before the class even began, I could tell we would have some logistics issues. Like almost every course I have taken at Berkeley, CS 287 was substantially over-enrolled at the start; we had perhaps eighty students before settling down to about sixty at the end. According to the CS 287 websites from previous years, it looks like the Fall 2009 and Fall 2012 courses had nineteen and fifteen students, respectively. Yeah, welcome to the new normal.

Due to the class size, Pieter actually provided two different lecture times, one in the morning and one in the afternoon, and I suspect he also convinced John to do the same thing for CS 294-112. Pieter did this to get to know the students better. During some of the class breaks, he would ask a handful of students to introduce themselves to everyone. Since I sat in the front corner of the room for optimal use of sign language interpreting services, I was called on first. From these introductions, I learned a few things from the class composition:

• There were a lot of mechanical engineering graduate students. So much, to the point where I was complaining (er, joking) about this with my interpreters midway through a long sequence of mechanical engineers introducing themselves. It’s a good thing that no one else in the class (I think…) can understand sign language. (PS: to mechanical engineers reading this, I was joking so please don’t get angry.)

• A lot of the students do not speak clearly! Many are quiet, have heavy foreign accents, or exhibit both qualities. The most egregious case resulted in my interpreter not understanding a single word a student said, which I mentioned earlier here.

• A lot of the students did robotics research of some form, whether it was in computer science, mechanical engineering, electrical engineering, or a related field. Then I’m confused, is it just this year that robotics suddenly became popular? Or is it because CS 287 wasn’t offered last year and that this is the “overflow” year?

In terms of course material, CS 287 combined lectures on standard topics in artificial intelligence (e.g., optimization and probability) and on more obscure, robotics research subjects. The course lectures could be divided as follows: Markov Decision Processes, optimization, probability, and research. Overall, I felt that the lectures were polished and of high quality. Pieter seemed like he really knew the material and was able to offer many doses of intuition for some of the more technical material.

I discuss this in my other reviews, so I’ll continue the trend: how did the lectures mesh with sign language interpreting services? Pieter lectured at a fast pace, which was problematic for my two interpreters, who were often exhausted when their 20-minute shifts were up. On the positive side, Pieter spoke loud and clear, to the point where I actually think he’s one of the easiest people for me to understand. Consequently, relative to other classes, I did not have much difficulty in terms of identifying the exact words he uttered. It’s also somewhat ironic that he would be the one to mention to me about an ideal future where people had “virtual captions” projected out of their mouths, which displays the text they say in real-time. Yes, I would like for that to happen.

As an added benefit, the course slides contained a lot of information. In many cases I could understand a concept or a homework sub-problem just by reading the appropriate slides, which is really handy for a text-heavy person like me. Incidentally, while Pieter wrote a lot of math on a white board, in almost all cases it was math directly from the slides, and he was writing it out for intuition. Thus, taking hand-written notes is probably unnecessary for this class.

No course is without its hiccups, however, and I’d like to bring up a few points that may (or may not) matter to future students:

• The difficulty of lectures varied considerably, which one can probably tell by browsing some of the slides. I thought the easiest class was the one on introductory probability. Since the material is quite rudimentary, I think that lecture needs to be eliminated in future iterations of the course. Basic probability is an ironclad requirement for understanding the math of robot systems. Other lectures were more complicated. The convex optimization and Kalman Filtering lectures would have been hard for me to follow had I not already had substantial exposure to those concepts.

• Towards the end of the semester, we had a “project speed-dating” lecture, which is when we gathered in small groups and shared our progress on the final project. Ideally, students could get feedback and learn what others were doing. In reality, most students skipped this class, and I’m not sure how beneficial it was to those students who did attend (I didn’t benefit). Furthermore, we eventually had final project presentations. Thus, I think project speed-dating should be replaced with a “standard” robotics lecture.

• We had three class sessions where guests from industry lectured about their companies. I’m neutral towards these, and would suggest that these only happen when Pieter (or another future instructor, if applicable) is traveling and unable to lecture.

CS 287 had four problem sets which involved math and MATLAB programming. I thought they were, on average, less challenging compared to problem sets in other classes. The math did not require incredible problem-solving skills, and I think they were designed to accommodate people from other fields (mechanical engineers …). For instance, the fourth homework asked to prove that covariance matrices are positive semidefinite, which is something that a lot of machine learning students can answer in thirty seconds. For the coding, we had to fill in MATLAB code in the designated “YOUR CODE HERE” sections. We got a lot of starter code for these assignments, so it’s relatively easy to understand how the code works in the overall pipeline.

To turn in homeworks, we used Gradescope, a company Pieter co-founded with Berkeley students. We only had to turn in PDFs of our answers, and the course staff can grade code-based assignments by spot-checking our plots. (Part of the reason why we had lots of starter code is because some of that is used to generate plots, which means that they are standardized across all student submissions.) We had page limits for our solutions, so be sure you know how to cram lots of figures together in LaTeX, such as by using minipages or subpages. Oh, I should mention: there are no solution sets to these assignments. I agree with Pieter in that there would be too much temptation for students to search for old solutions. Well, I wouldn’t search, but I’m not sure about others.

In addition to regular homeworks, we had four (!) optional extra credits, plus the final project. I only did one of the extra credit assignments, so I don’t have much to comment on those.

For my final project, I worked on a deep learning project about Atari game play, but my project ended up relating more to human learning since I analyzed data from humans playing Atari games on Amazon Mechanical Turk, and I ran out of time to integrate my findings with a Q-Learning agent. Pieter was the one who suggested this project. In fact, back in October, he and the two GSIs actually met with every project group in the class for five minutes to discuss the final project. Then, a day later, I assume Pieter sent out personalized emails to every group with project suggestions. That must have been a lot of work!

Just like in CS 280, we had project presentations, not a project poster session. That is a good thing. Single-student groups presented for 5.5 minutes. I tried to be funny by sprinkling in four jokes in my talk, and went so far as to put in a picture of Bernie Sanders in one of my slides. Unfortunately, I think my Sanders-related joke backfired since a lot of the students were internationals or were not fluent in American politics, whereas I have very strong political beliefs.

We then had to write the usual report to wrap up the project. I will warn future students: the grading for the final project is somewhat stricter than the grading for homeworks, though admittedly I think it was hard to get a really low grade on the project. Thus, to get an A, try to get at least 90 percent of the homework points, and make up for lost points with the four extra credit assignments. Pieter really makes it clear how our grades are computed, which makes the process less stressful for students who care about grades. This is in contrast with some other professors, who might not even return grades for final projects.

In conclusion, I enjoyed CS 287 and would highly recommend it to future students. Again, if possible consider taking this class concurrently with Deep Reinforcement Learning or a similar two-credit class as they would reinforce each other.

Update October 31, 2016: I received an announcement that CS 294-112 will be taught again next semester! That sounds exciting, and while I won’t be enrolling in the course, I will be following its progress and staying in touch on the concepts taught.

And by the way, today I finally published my reinforcement learning post that I said I would write in my July update. You can see it here.

Update July 18, 2016: This post seems to have gotten a considerable amount of attention, at least compared to my normal blog posts, so I would like to answer some of the common questions that I’ve received in either the comments or by private email.

1. If you’re looking for homework assignments, I first want to warn you that, as I emphasize in the my review, the assignments are probably not going to be as educational as you would want them to be. If you’re still interested, our TA for the class posted a github repository on the Berkeley RLL page with the homework for this class. The homeworks are iPython notebooks (now called Jupyter notebooks, I think). If there’s code in the “YOUR CODE HERE” sections, then you’re probably reading the solutions; I’m not sure if there’s a clean version of the assignments there.

2. Unfortunately, we did not have any video lectures, slides, or readings outside of what you can see on the class website. A note for those who are reading the comments after this update: the class website was originally pulled down due to “some tyrants” (according to the course staff), but it’s happily now up.

3. If you’re looking for other resources to learn about deep reinforcement learning, I have several recommendations. In terms of courses, check out David Silver’s reinforcement learning course and the recent Machine Learning Summer School; the latter had our class instructor as part of the course staff, so the material is probably going to be similar to what we covered. (Coming up in a few weeks is the Deep Learning Summer School, something you might also want to check out.) I have all these courses bookmarked and am trying to carve out some time to read the slides. In terms of code, I would strongly recommend starting with either the deep_q_rl library or OpenAI Gym. The former is a super easy-to-read Python library that allows you to replicate DeepMind’s results in their 2013 and 2015 papers on Atari games. The latter was recently launched, and I don’t have experience with it, but it sounds really cool as we can compare our reinforcement learning implementations.

4. This is more of a comment than an answer, but I thought I’d mention it anyway: my blog’s comments are handled by Disqus, and in the moderation panel I can see the emails of the commenters. Thus, there is no need to post your email publicly as I can see it regardless.

Thanks everyone, and that’s all! After this paragraph is the original post as I had written it. But one more thing: after rereading this post, I think I was a little too harsh on the class. Furthermore, even though people have said they liked this post, I don’t think I gave reinforcement learning its due. So to rectify my regrets, I’m planning on launching a new series of deep reinforcement learning posts on this blog, similar to the style of Andrej Karpathy’s excellent blog post. I’ve already written a post on basic reinforcement learning, so I’m hoping to progress towards more advanced topics. My goal is to have the first post up sometime in August. Hopefully those will be a good resource for some enthusiasts out there.

What is this course? At the time I enrolled, it was a new two-credit class called Deep Reinforcement Learning (CS 294-112) and taught by Pieter Abbeel’s graduate student, John Schulman. It seemed like a cross between a research seminar and a normal lecture course. The former tend to be one or two credits and are principally about relevant research results; the latter tend to be three or four credits and have lectures, homeworks, exams, and projects.

In AI and robotics, reinforcement learning is a standard way of framing a problem. For example, if a robot needs to learn how to play a game, it must engage in “reinforcement learning” to try out different actions, get rewards, and then modify its policy. The word “deep” refers to how deep neural networks have recently become the workhorse of state-of-the-art reinforcement learning. (This is why the class wasn’t taught until now.) The broader category of deep learning involves the use of deep neural networks in other applications, such as image classification and speech recognition. Deep learning has become so popular that Google even paid $400 million to buy a deep learning company, DeepMind.

The class had about eighty students, so to avoid getting into trouble with the building managers about stuffing too many people in one room, John gave two identical lectures for each class day. I remained in the afternoon session to make it easy on the interpreters’ schedules, but unfortunately, most of the other students picked the afternoon session, but hey, they don’t have my excuse … perhaps they can’t wake up early? So once again, a graduate level class had some of its students sitting on the floor. Seems like that’s a common problem here, huh?

Anyway, back to the class discussion. The first few lectures were about Markov Decision Processes and neural networks, so if there were any classes to miss, it would be those because I already knew the material.

The remaining lectures were, to be frank, difficult, and I often felt mentally stressed in class. Most of the content was pure math, and the derivations were a long sequence of sums, expectations, and other terms, each of which were more sums and expectations. For instance, look at the formula for policy gradients:

To understand¹ this, one has to process lots of material, such as what it means to take the gradient of the log of a policy, and that \(\Psi_t\) isn’t just a simple scalar but can represent concepts like the advantage function, which involves another sequence of expectations and sums of rewards. Connecting this material is challenging in real time, and I felt that the lectures did not provide sufficient intuition. My sign language interpreters tried to repeat the exact words John uttered, but despite this, I could not translate this process into clear mathematical comprehension.

Given that the lectures were difficult for me to follow, I hoped that homeworks would be more useful. The homeworks in this class were provided as IPython/Jupyter notebooks. We had starter code and needed to fill in the “YOUR CODE HERE” sections.

The first homework was nearly trivial for people who knew about the basics of Markov Decision Process, Value Iteration, Policy Iteration, and Q-Learning. I wrote about thirty lines of Python code for the entire assignment.

The second homework, on policy gradients, was more interesting, but the release date kept getting postponed. It soon became a running joke in class whenever John said: “Oh, and about that second homework, we plan to release it in a few days…”. It was finally released on October 11. (John on Piazza: “You may have given up hope that this day would ever come, but behold, HW2 is finally here.”) To put this in perspective, the first homework assignment was due on September 7.

Fortunately, the second assignment was more challenging than the first, and I had to be careful in implementing formulas since math from research papers doesn’t always translate neatly into code. I was pleased to see that the homework was designed so naive implementations of formulas would take too long to test. (I believe AI assignments should require code to be reasonably optimized.)

We were going to have homeworks on approximate dynamic programming and supervised learning, but since the second homework got delayed so much and the third one would have taken too long to create, the staff canceled all future assignments.

To be honest, the main deep reinforcement learning material I learned this semester didn’t even come from this class. In Pieter’s Advanced Robotics (CS 287) class, which I also took this semester, my final project was about deep learning for Atari games. I had time to sufficiently read and absorb the Atari deep learning research papers, which helped me to better understand some of the material in this class (CS 294-112). Consequently, my recommendation for someone who wants to take this class in the future is to, if possible, take CS 287 concurrently and do a project that uses neural networks. That way, one gets to do deep reinforcement learning.

To recap, here are some of the positive aspects of the class:

• It covers a popular and interesting research area.
• It presents many relevant research papers, including those from Berkeley students.
• For a class that is almost like a research seminar, there are many online resources one can consult for additional background. Unfortunately, a lot of the written references are also hard to understand.
• It is easy to obtain homework help on Piazza.

Here are some of the negative ones:

• The lectures were not polished and involved lots of math without intuition. This issue is understandable because it was a first time course taught by a graduate student.
• There did not seem to be much advance preparation for the course in terms of lecture material. The course website had a brief outline of lectures, but we had to change some of that on short notice.
• It did not provide sufficiently many or sufficiently difficult homework assignments. Having more in-depth assignments would let me deeply reinforce my understanding (pun fully intended).

Ultimately, this course allowed me to scratch the surface of deep reinforcement learning, though it was immensely frustrating for me to try and understand the material directly from the lecture, and the haphazard nature of the course did not help. I suspect that future iterations of the course will proceed more smoothly, and yes, even though no one’s told me personally, this class will be offered again (in some form) so long as deep learning remains the king of machine learning.

Well, I finally did it. I submitted my last homework assignment for this semester, the fifth one for convex optimization. The only work I have left to do this semester are my final projects.

As I was handing in the assignment, I once again wondered about a related question: how often do students work together on problem sets? My focus is on graduate-level computer science problem sets (or those from related fields). I’ve thought about that a lot this semester, since it’s a subset of the theme that I now think about every day, every hour: isolation.

I spent much of my summer alone in my “shared” office in a deserted VCL lab on the fifth floor of Soda Hall. While the other students had summer internships at Microsoft and Google, I was sitting there from 8:00AM to the evening, staring at my laptop, trying to do research, but often giving up and instead doing some prelim preparation (and blogging about that, of course). The extent of my daily conversations¹ would sometimes be when I talked to various cashiers working at the cafes on Euclid Street, because I had to say things like: “I would like to buy X and Y. Thank you.”

That was it for the day (including evenings and nights, by the way).

The isolation I was experiencing gradually consumed me throughout the summer and adversely affected my mood and ability to focus. During the week before, during, and after the prelims, I regularly lost whole days of productivity because I was thinking about isolation all the time and how I wished I had other students with whom I could talk. (Fortunately, the prelims themselves were pretty easy, in part because I did a lot of studying before those “lost days” occurred.)

I still haven’t been able to completely recover from that disastrous summer, but I’ve made some baby steps this semester, and one of those steps has been to reach out to other students for homework collaboration.

This is new for me. In college, I did most homework assignments by myself, and made heavy use of office hours for the professors and teaching assistants. I continued that trend during my first semester at Berkeley, but that did not turn out so well. Last spring was much better, because in computer vision, we were allowed to work in groups of two and submit as a group (i.e., not “work and then submit separately,” which is the usual case) and I actually had a homework partner. He was the one who initiated our collaboration.

With that positive experience in mind, I tried to actively contact other students this semester. I sent more emails and initiated more conversations about the homeworks, and I did benefit from the discussions I had.

But I couldn’t help but think: is this the normal way students work together?

I think about this because I see many groups of students that are consistently together: they attend classes together, they attend GSI discussion sections together, they walk together, they eat together, and they do all sorts of social events together. To me, this indicates that they do not have to rely on the “email, suggest several times to meet, etc.” tactic that I used to discuss homework with classmates.

In other words, I’m someone who discusses work with other students by setting up meeting times; I sometimes feel that other students are just together all the time and don’t have to do that.

Would I like to be able to have that experience? Well, yes, of course. Sadly, working with other students doesn’t always end up working well. I don’t mean “not working well” in the sense that we can’t figure out something; I refer to “working well” in the context of how I feel after a group meeting. For instance, I thought I had an incredible stroke of luck when I found that someone else in my convex optimization class wanted to discuss practice problems to prepare for the midterm. I hastily replied, saying yes. Unfortunately, that discussion had four or five other students there and I could not hear much of what they were saying, so I felt lousy. I left early, wishing that I had specifically requested a one-on-one meeting.

The lesson? I have to be careful about working with other students, and to mentally calculate an extensive cost-benefit analysis.

Anyway, those are just some random thoughts I have now. I hope next semester will be a lot better than this one.

I just submitted a sign language interpreting services request for the spring 2016 semester, when I am likely to take EE 227C and CS 267. The former is the third convex optimization course offered at Berkeley, and the latter is a popular entry-level graduate course on parallel computing and systems.

For this request, though, I also said that I wanted to have a more consistent group of interpreters. This means I would prefer to have the same interpreters currently working now (or those from last semester) to be assigned to those two courses. Just like in the Spring 2015 semester, I have a standard group of three to four interpreters this semester, but strangely enough, none of them were also part of the Spring 2015 group. This is despite how all of the interpreters are assigned out of the same Bay Area company, Partners In Communication LLC.

In addition, there’s been another interpreting issue for this semester in particular. I’m not sure why, but I have had an unusual amount of substitutes. There are two primary interpreters, plus one primary substitute interpreter, but then there have been at least five cases (as far as I can remember, all involving different people) when I’ve had substitutes for substitutes.

This would be frustrating even if I was taking an undergraduate humanities course, but when the material is so technical in my courses, a normal person cannot convey the material clearly on day one. At least with consistent interpreters, they can pick up some of the common terminology. The people who interpret for my Convex Optimization class (EE 227BT) have gotten so used to hearing the words “positive semidefinite matrix” together that they can now understand that sequence when it’s used in other classes. (Positive semidefinite matrices are everywhere in machine learning – I can’t believe I went through undergrad without knowing about them, and now I’m one of their biggest fans.)

Consistent interpreting is something that I admittedly did not think about when requesting for services last semester, but I will remember this for the future. It is already challenging for interpreters to work in STEM courses, so there needs to be consistency so that they improve throughout a semester. Note that in general, I do benefit somewhat from interpreting services despite issues in STEM courses, and in some cases interpreters are essential (as was the case a few weeks ago when an ear infection meant I had to stop wearing my right hearing aid for a week), so this is pretty important to me.

Oh, speaking of interpreting requests, I also need to hope that no one else “strongly suggests” me to drop and/or add a course at the last minute, though admittedly, adding a course results in substantially fewer headaches as compared to dropping a course.

Lately, I’ve observed an interesting phenomenon when my sign language interpreters have a tough time understanding some of my classmates’ accents, yet my professors (and, presumably, my other classmates) don’t seem to have that problem. Here are a few non-exhaustive examples, restricted to my Berkeley experience:

• I once gave a talk in Peter Bartlett’s research group meeting back in April. I had a sign language interpreter there, and she was able to help me by explaining some of the comments Peter made about the paper during pauses in my lecture. Unfortunately, she had major trouble with one of the postdocs, who had an accent I couldn’t even distinguish – it was not Chinese or Indian. She was unable to explain what that person said, and I think we had to rely on a few other people to help us out, plus a couple of finger pointing to the relevant stuff I wrote on the whiteboard.

• In my EE 227BT class (Convex Optimization), many of the students are Chinese. My interpreters had such a hard time understanding some of them that, after the first few lectures, they talked to the professor, Laurent El Ghaoui, about it. He acknowledged that some of them were tough to comprehend (“they’re engineers” he lamented) but he learned to repeat their questions so that my interpreters could easily relay the information back to me. However, there lies the interesting factor: my interpreters sit pretty close to the professor, and he doesn’t move around too much in class, so the difference in their comprehension probably doesn’t come down to distance from the speaker.

• In my CS 287 class (Advanced Robotics), Pieter Abbeel is unusual in that he seems like he really wants to get to know the students. (Our class is much larger than the previous editions, so he actually offers two lecture times to reduce the number of students in a room!) During some of our class breaks, he will take out the list of students and ask some of them to stand up and introduce themselves to the rest of the class. When one of the Indian students spoke about himself, my interpreter could not understand a single word that student said – literally! But Pieter did not even ask that student to repeat himself, so I assume he must have understood part of what that student said. This situation happened to a less extreme event (as in, the interpreter understood a handful of words) with a few other students.

I think the only way that can explain the comprehension disparity between my interpreters and professors is that the latter group of people are more used to being around foreigners. I wrote a blog post almost three years ago that highlighted my concern over understanding foreign accents in graduate school. Unfortunately, it’s been a nontrivial problem for me here as most of the students I work or converse with are international students (typically from one of two major countries: China or India).

Incidentally, none of those three professors are American¹, so it’s possible that they may be more skilled at picking up accents since they’ve traveled to quite a number of places and conversed with lots of people. That’s my only explanation. But I would also be interested in knowing if there was any initial struggle or hump they had to clear, or if they actually do have trouble understanding people but are clever at hiding it.

So, here are some questions I’d like to ask:

• To people who can understand foreigners easily: why do you feel like this is the case? Where are you from? Have you traveled around the world a lot, talking to people of different nationalities? Was it always easy to talk to foreigners?

• To people who have a hard time understanding foreigners: do you get the chance to talk to a diverse group of people? How long have you tried to understand foreign accents?

• To American STEM students: how good are you at communicating with foreigners? Do you find the high proportion of foreign students in STEM to be a deterrent to your education?

• To foreigners: do you get frustrated when people ask you to repeat what you say? What are your thoughts in particular about communicating with deaf people like me (who have enough hearing to talk one-on-one)?

The practical concern of this for someone like me is that, if I work in a group of foreigners – reducing the likelihood of one-on-one conversations – will there be any benefit of a sign language interpreter?

It’s nice that Berkeley has an access services page that I can use to request accommodations. But it’s not perfect, and there are several things that really should be fundamental components of any service request system. Here are some of my “fundamental components,” which are not currently part of Berkeley’s recently-overhauled system:

• Any time I submit a request form, I need to get a “receipt” email that confirms I sent the request, along with the details. This gives me proof of submission and protects me in case Berkeley’s DSP loses it somehow. It also lets me double check that I filled in the boxes with correct information – it’s easy to mess up on these things.

• Any time the requests are satisfied, I need to get an email telling me that information. In my case, this means a sign language interpreter (or two) got assigned to wherever I am going, and I should know their names and contact information. Last year, for instance, I made a request for interpreting services for the Berkeley EECS town hall, but I ended up getting captioning instead, and I didn’t know until the last minute (well, five minutes). The town hall ended up being a disaster, though to be fair, it would have been difficult for an interpreter to be effective there given the noisy atmosphere.

• In the request form, there needs to be a generic “describe any miscellaneous information” box that I can type in to describe such information. For instance, some events may last for hours, but are low-key and don’t involve much discussion. If DSP were to just look at a request for a two-hour event, they would automatically hire two interpreters, but sometimes I might have to make it clear that only one is needed (thus saving money and man/woman-power). I’ve had to resort to describing this information to the person managing the requests by email, and that’s cumbersome.

I might be stretching here, but it would also be nice if my requests could get processed over the weekends. Like many graduate students, who are young and consumed with work, I don’t make much of a distinction between weekdays and weekends. But DSP will not operate over the weekends since they are staffed by “real world workers.” (Just to be clear, that’s a jab at graduate students, not real world workers.) Consequently, I have to be careful to submit requests before Friday evening; otherwise, DSP doesn’t get to look at them until Monday morning. I’ve been burned on this at least once. The lesson? Plan way ahead. I don’t have the luxury of going to an event on short notice.

My weekend idea is probably a bit too much to ask. I would be satisfied if DSP could implement my three other suggestions.

I would have thought that these things I mention are obvious, but I guess DSP didn’t have anyone complain, or they’re having technical difficulties. At the very least, this situation serves as yet another reminder to me that I need to educate intelligent people who have never considered the various issues that arise for deaf people.

A few weeks ago, there was a Berkeley AI social event. My natural reaction upon finding out about this was to ignore it, due to deeply unpleasant experiences in social gatherings before. Yet, I ended up going, due to two reasons. The first was that I had a terrible summer and was constantly in a bad mood, so I figured that even if I hated attending the social, my resulting mood couldn’t possibly be worse than what I was experiencing on a daily basis. The second reason why I attended was because John Canny said he would be going there, and he invited me to go with him. This would at least reduce the likelihood of the most common situation for me in social events: when I stand around awkwardly, watch other people talk without a clue as to what they are talking about, and then leave when my level of frustration exceeds a certain threshold.

Critically, John and I would be going together, not separately, so my plan was to stick with him until he either introduced me to someone, or until someone were to start a conversation with me. In the latter case, I would immediately switch to communicating with that person since John would have no trouble finding others to talk to. My goal for the AI social was to have at least one non-trivial conversation (ideally at least ten minutes) with someone (other than John), and leave with my mood at least as good as it was beforehand.

Well, fortune struck that afternoon. I had three (yes, three) such conversations! And I have an embarrassingly detailed recollection of how these conversations began, and what we talked about – often down to the exact words and sentences we said.

For the sake of privacy, I won’t go through all the details, but here is the high level story. When John and I went to the social event, there was already a huge crowd of faculty and students that I immediately became worried. Fortunately, there was a quieter room to the side that a few of us were in, and I was able to make my way over there. I saw Trevor (hey, can you tell me my prelim score already?) and a few other familiar folks. I had just started enjoying my cup of red wine when another student saw me and started a conversation, my first real one for that event. Fortunately, he spoke clearly, and the “side room” was sufficiently quiet.

I believe we had a nice conversation (I hope he liked it), and again, for the sake of privacy I won’t go through the details (but I can probably produce an accurate transcript of our conversation if needed). We reached a good stopping point, and then split up. I got some additional food and wine, and returned to the more crowded area. I was now by myself in a painfully familiar situation, and planned to remain only briefly.

But I got lucky – someone was walking back to work, and saw me along the way¹ so we ended up talking. Again, this was another person who I knew somewhat well, and his voice is easy to understand. Our conversation was also pretty nice. We discussed the prelims and his plans for the next few years.

Then he had to leave. I stood around by the now-empty plate of food, and was getting ready to head out when I got lucky again: a student who I had seen before was walking towards me and had made eye contact. Yay! I did not know him as much as the two earlier students, so our conversation veered towards standard “introductory” material.

By the time we finished, most of the other students and faculty had left to go back to work (or home, because it was Friday evening), so I figured I would do the same.

But wow, that event was something I will definitely remember for a while. I felt so deliriously happy after the social, that it actually ended up a net negative on my work progress for the rest of that evening, because I kept thinking about the social rather than my work! (Don’t get me wrong – this was the rare case when I was happy not to get work done.) If others knew how much I obsess over almost trivial conversations, how I have a near-transcript level of conversation recollection, and how often I replay social situations in my head, they would probably be shocked.

So should I try attending social events more often? Maybe. Actually, one of my concerns is if I set expectations that are too high for future social events. I guess that’s not the worst thing worry about, though.

After a year into my doctorate program at Berkeley, I know that my experience has been suboptimal in many ways. One reason for that – actually, the main reason – is because I have been experiencing severe isolation the past few months, primarily a product of being in a small research group where I feel like my research interests and career goals do not closely match with those of the other people here.

Yeah, it’s “the usual” for me. After middle school, I badly wanted a fresh start in high school so that I could cut down on all the isolation I had experienced. Then I badly wanted a fresh start in college, for similar reasons. Then I badly wanted a fresh start in graduate school, also for similar reasons.

So my wish for the 2015-2016 academic year is simple, and I hope, realistic.

I wish … that I will be able to find another true, student collaborator, someone who is also a Ph.D. student here, and is interested in Artificial Intelligence research. Someone who will be willing to sit down with me, work with me side by side, and help teach me what it is like to do true research and boost my confidence. Someone who will not mind if I mess up on minor errors. Someone who has good English language skills, who can speak clearly, and who will not mind that I am deaf.

Someone who I can consider a true friend.

Note: I wrote the following “transcript” of my exam from memory, so it should not be taken as verbatim.

Before the Exam

Of the twelve AI students taking the prelims this fall, I was up last to go; my times were 4:10 to 4:40 with Pieter Abbeel and Dan Klein, and 5:10 to 5:40 with Ruzena Bajcsy and Trevor Darrell. Obviously, I had spent the entire day of August 24 before 4:10 doing some last-minute preparation. I arrived in the seventh floor of Sutardja Dai Hall and met my sign language interpreter there, who was relieved that she hadn’t gotten lost or sent to the wrong location.

Actually, I should backtrack to rant a little. My prelims was yet another example of how having multiple channels of communication in setting up a sign language interpreting appointment can mess things up. A week before the prelims, I carefully prepared a three-page document of preparatory material for my interpreter to review. Most of the document was a list of advanced terminology that she might expect to hear on the prelims. My goal was for her to look at the words, remember the spelling, check the pronunciations online (if necessary) so that she could finger-spell them quickly¹ during the prelims. I also listed where and when we should meet before the prelims. Finally, and this is important, I gave the document to Berkeley’s DSP, who then forwarded it over to the agency that officially appoints the interpreters.

Yet when I arrived in the location where I requested to meet (the third floor of Sutardja Dai Hall), I never saw her, and when it was 4:05pm, I had no choice but to go up to the seventh floor. It was only when I finally got near Pieter’s office that I saw her. She then said that she had never gotten that document I created. This is the problem: I specifically asked to send my prep documents to the interpreter directly – not through multiple parties – but got declined². We lost a bit of early discussion time: she went right to the location of the exam at 3:50pm, while I was anxiously pacing around in the lobby waiting for no one.

In the end, this might be me going overboard, since the prelims are not a case where having interpreters is strictly necessary for me. I can understand most people when they talk clearly and directly to me, but there are many other situations when having informed interpreters would be vital.

Sorry for the rant. A few minutes after I arrived near his office, Pieter came out and immediately told me to come in. It was time.

Part One

“So … hello,” Pieter and Dan said simultaneously.

“Hi,” I replied. I had never seen Dan and Pieter look like this before, though admittedly I do not know either of them that well. I think they were either super-tired after having eleven other students before me, or they were trying super-hard to make me feel less nervous.

“The prelims are going to be a little different this time,” Dan said, “but everyone is doing the same thing, so don’t worry. It’s a written exam. You have thirty minutes to answer these questions. You can say things out loud if you already know the answer, and you don’t have to show excessive work. While you do that, I will take notes on my laptop, so … try not to worry about me.”

Fat chance, I thought as he smiled awkwardly. Dan pressed the timer on his phone, starting the exam.

I opened the exam and flipped through all the nine questions to get a feel for them. Then I went back to the fifth question, about logic, since I knew the answer already.

“Well, the term \(\alpha \models \beta\) just means alpha entails beta, which is the same thing as saying that \(\alpha\) implies \(\beta\),” I said, writing down briefly. “And an algorithm for doing that is resolution. Or if we’re assuming Horn or definite clauses, we can use forward chaining and backward chaining.”

Both of them nodded. Since that was the extent of the question³, I went back to the start of the exam, in an attempt to do the rest of the questions in order. The first question was about different search algorithms and heuristics. The graph was structured as a directed tree with two goal states, with (different) edge costs listed for each arc.

“For depth first search, we just go to the left,” I said, outlining the path. “For uniform cost search, we expand this goal state. For a heuristic, we just need to not overestimate to the goal. And for the last part, when we talk about ranges that would make the heuristic admissible, it seems like we just need to make sure we have that be at most four … wait, we are doing A-star search, right?”

“Yes,” Pieter said. “Think about the value 4.5.”

I nodded and wrote my answer formally on the sheet. Then I moved on to the next question, about constraint satisfaction problems. What happens if we enforce arc consistency, and (1) we have one element in each domain, (2) we have a variable with no values left, (3) we have multiple values in each domain? “The first one should have an immediate solution,” I said. “For the second case, we’re guaranteed not to have a solution. For the third, we are not guaranteed to have a solution.”

Dan and Pieter did not noticeably react, so I went on to the third question. It presented me with a tree and asked me to write down a set of leaf node values so that the expectimax versus minimax paths are different. That was easy for me, as I wrote down “1,” “1,” “10,” and “0” for the two sets of two leaf nodes (so four leaf nodes in all). Both of them nodded in approval.

The fourth one was about Markov Decision Processes, and involved substantially more text than the previous questions. I looked at it and decided to move on to the sixth question.

“Oh yeah, a lot of people skipped that one,” Pieter said. I did not ask if that meant they skipped and solved it later, or (gulp) if they skipped it entirely.

The sixth question (remember, the fifth was about logic) presented me with two Bayesian Networks. The first part, asked me to write down the joint (that’s easy – just multiply \(P(X_i \mid {\rm Parents}_{X_i})\) values together). The second was slightly more challenging, which asked me to outline a good variable elimination ordering and a bad variable elimination ordering. The graph was shaped with a root node \(X\) connected to \(Y_1\) through \(Y_n\) and there were also “\(Z\)” nodes downstream of the \(Y\) nodes.

“Obviously, a bad elimination ordering starts with \(X\) because if you eliminate it, all the \(P(Y_n\mid X)\) terms get put into one factor that depends on all the \(Y_n\)s, so you get a giant table,” I said. “Now, for a good variable elimination ordering, eliminate \(X\) last. Then I guess the only question is whether we should eliminate \(Y_1\), \(Y_2\), and so on, or the other way around. To do that …”

“You don’t need to do that,” Dan interrupted.

“Oh, I guess the ordering of the \(Y\)s doesn’t matter,” I said. I probably would have figured this out eventually, but I’m glad they were helping me to speed up.

The seventh question presented me with a familiar decision network diagram. “The oil can be in one of three locations,” I muttered out loud, reading the question. “One hundred utility for getting the oil, zero for not getting it. So the MEU with no information is just one hundred divided by three, since one third of the time, we get 100 utility and otherwise we get nothing.”

The second part asked about the VPI of knowing with certainty the state of oil in one of the three locations (i.e., it was either “there” or “not there” with certainty). “For that, we need to find the maximum expected utility with this information, minus the MEU I found from the first part,” I said. “So one third of the time, we know the oil for certainty, and two thirds of the time, we can narrow down our options to the other two. So subtracting that off … it’s fifty over three.”

The eighth part was about maximum likelihood. Given that we have heads, heads, tails, and heads, I had to show that the MLE of \(P(H) = 3/4\).

“The standard way of doing this is to write the product of the Bernoullis and form the Lagrangian …” I began, but Dan correctly pointed out that it wasn’t going to be that complicated.

“Oh yeah, we can literally write out \(h^3(1-h)^1\),” I said, writing it out. Unfortunately, I ended up getting \(P(H) = 1/4\). I stared at my algebra for an embarrassingly long time before Dan pointed out my stupid error: failing to distribute a “3” appropriately.

“Yeah, that’s right,” I said, relieved. “Moving on…”

The last question (well, second last for me) showed me three different two-dimensional Gaussian distributions, with different \(\sigma\) “curves” printed. I never saw these diagrams before but it was pretty intuitive what it meant; if the curve stretched “long” in the \(x\) direction but “short” in the \(y\) direction, then the covariance matrix would have \(\Sigma_{1,1} > \Sigma_{2,2}\). Two of them had diagonal covariance matrices, and the third one, which stretched out long in the second and fourth quadrants, I put down as having \(Cov(X,Y) = -1.5\).

“Why did you pick that?” Pieter asked.

“Well … “ I said, not entirely sure if that was correct. (I later realized after the exam that I was right, and knowing that with certainty required remembering the formula for correlation.) I wrote out the definition of the covariance: \(\Sigma_{1,2} = Cov(X,Y) = \mathbb{E}[XY] - \mathbb{E}[X]\mathbb{E}[X]\).

“And the expected values of both are zero,” Pieter pointed out.

I wasn’t sure if he said that in agreement with my answer, but time was running out so I came back to that MDP question I skipped earlier (and left my answer to the ninth question unchanged). There was a grid of squares arranged in a “circular” fashion where we could move to any of two adjacent squares, except for two “slide” locations that forced us to move right.

“This is asking me about the value of states after three, ten, and infinity iterations of Value Iteration, with discounts of \(\gamma=1\) or \(\gamma=0.1\)” I said. “Well, the value of the state by the slide is going to be two plus two-tenths after three iterations with discounting. Without, it’s four.”

I proceeded, figuring out the different values of states they asked me to write. I tried to sprinkle in a few jokes here and there to amuse them, and was moderately successful. Unfortunately, time ran out before I could fill in the last two blanks, so I put in a “2” in one of the boxes at random.

“Are you sure about your answer to that one?” Pieter asked.

“No, I only put a random value down to get something down in the time limit,” I said.

“Well, why don’t you try and solve it?”

I looked at it, and within a few seconds, saw that the answer was infinity. “Um, yeah, infinity I guess, for both” I said, knowing that I should have gotten that earlier.

“All right, I guess we’re done. You’re the last one so you can now talk to any of the other students about this part of the exam,” Pieter said.

“Do you have a rough idea of how well I did?” I asked.

Dan smiled awkwardly. “We … can’t really do that now.”

Fine, I acknowledged, and left the office feeling reasonably happy with my performance. I read my AI book for a few more minutes before showing up at Ruzena’s office.

Part Two

“Well, hello. Why don’t you introduce yourself?” Trevor asked. Again, I’m assuming they were doing this to help the students feel less nervous, though in my case I did not expect these two to know anything about me so this really did qualify as an introduction. I mentioned my undergraduate institution and my advisor, but I also wish I had remembered to say that I was deaf since birth.

Then they proceeded to ask questions.

“Explain logistic regression,” Trevor said.

“This is a classification algorithm,” I replied. “Let’s suppose we’re in the binary classification case. Then logistic regression means that we are assuming – at least in the discriminative case – that our data should be assigned probabilistically to classes of 0 or 1 based on the logistic function, \(P(y = 0\mid x, \theta) = (1+e^{-\theta^Tx})^{-1}\).” I wrote the formula on Ruzena’s white board.

“And what are the parameters?” Trevor asked. I pointed to \(\theta\) and mentioned that we could update these with a stochastic gradient method based on the gradient of the data log likelihood.

“Next up: how do you do linear regression on a V-shaped data?” Trevor asked.

“This is a mixture model,” I said. “Just have different linear regressions for the two sets of data.” I drew some hypothetical data on the board.

“But how do you know that you will have two components?” Trevor asked, shrugging. “Why not just one regression line?”

“Well, this is basically ordinary least squares, right? So with an extra regression, we would be able to better minimize the sum of squared errors…”

“Perhaps I should rephrase this,” Trevor said. “We have to decide the number of components, and in the general case, we can’t just eyeball the data and say that we will have two components. We need to try out different models and evaluate them somehow.”

“Oh, just try out different numbers of distributions in the mixture model and perform cross validation–”

“Yes, good,” Trevor interrupted. “Next up, how would you classify data if you did not know the labels?”

“One way to do that is with an algorithm like K-means,” I replied. I drew out some unlabeled data and tried to signal how the algorithm would work by mentioning how the center of each cluster gets updated.

“Is this parametric or non-parametric?”

“Uh … it’s parametric in the sense that we can fix \(K\) and we only have a finite number of parameters.”

“That’s correct,” Trevor said, “but what is an example of a non-parametric technique?”

“Nearest neighbors.”

It was Ruzena’s turn to ask. “Can you write down Bayes’ rule for classification?”

I wrote down Bayes’ rule on the white board, for \(P(y=0\mid x,\theta)\). I wasn’t sure if I really understood the question, because it’s just Bayes’ rule!

“Often times we care about learning the parameters,” Ruzena said.

“Yes, in which case we would have something like Bayes’ rule applied to \(P(\theta \mid x)\),” I said, still unsure if I was supposed to answer something in more detail.

“Can you write down or explain what the Bayes’ risk means?” Ruzena asked.

This wasn’t on the syllabus, I thought, but remembering the formulas from CS 281A, I wrote down \(\mathbb{E}[\ell(y,\hat{y})]\). “Basically, the expected loss between what we predict \(\hat{y}\) and the true \(y\).”

Surprisingly, they seemed satisfied with that brief answer, so Trevor changed the subject to the next part – neural networks⁴.

“First, describe a neural network.”

“This is a classifier that can also be viewed as an architecture,” I said, drawing out some nodes on the board. “We have an input layer that takes in our data, such as pixels in an image. Then we have the option of having hidden layers, and I’ll write down one. Then an output layer, where we have outputs. The key with these architectures is that the hidden layers allow for extra complexity, so to speak, but we also need to make sure we add in activation functions for the nodes to introduce nonlinearity. So we can use the sigmoid.”

I explained a few more basic properties in detail, and also went over backpropagation, until Trevor seemed satisfied.

“Now we’re going to talk about convolutional neural networks,” Trevor said. I kind of expected this to happen since Trevor was on the committee, but since CNNs were not on the syllabus, I would have to rely on my memory of CS 280 material (thank goodness I took the class).

“I have a network architecture listed here,” Trevor said, showing me his iPad. “Please draw it.”

I drew it out. It was a standard LeNet-like architecture, with a \(13\times 13\) input layer, a convolutional layer, a max-pooling layer, and a fully connected layer, resulting in four outputs.

“How many pixels are there in each resulting image in the convolutional layer, given the kernel size listed?”

“They are ten by ten,” I replied, since the filters were \(4\times 4\) and the stride was one.

“Good. Now what about the size of the max-pooling layers?”

“Five by five.”

“And how many weights are there in the fully connected part?”

I wrote down \((3\times 25) \times 4\) on the board.

“So, three hundred,” Trevor approved. “Now can you tell me the difference in run time or space time between convolutional and fully connected layers?”

“Yes, the space time is higher for fully connected layers because convolutional ones have weight sharing,” I replied, with Trevor nodding. “As far as runtime, wouldn’t the same apply for the convolutional one …”

“Well, think about the total amount of weights,” Trevor corrected.

I mutter something about the total number of (not necessarily unique) weights, and tried to make a high-level argument that the runtime would be higher in the convolutional layer, assuming that training or testing time would be proportional to the number of weights. Trevor seemed happy, and continued with asking neural network questions.

“Can you talk about the vanishing gradient problem?”

This was another topic that I only remember from CS 280. Fortunately, I did remember, and I wrote out the curve of the sigmoind function. “With the sigmoid, the gradient will go to zero as \(x\) goes to plus or minus infinity. After a certain point, the difference in gradients is irrelevant and will not contribute to the update. This is why we like ReLU layers, because those are \(f(x) = \max\{0,x\}\) and the gradient will increase linearly.”

I fumbled around with my initially sloppy explanation until I felt Trevor seemed satisfied with a less sloppy version.

“The last question for today is about transfer learning,” Trevor said. “What is it?”

Yet another question from CS 280! Wow, I am really glad I took the class. “That’s when we use weights learned from one task to apply to another task, hence transferring the knowledge from training one thing to another. So, in a computer vision object recognition challenge, imagine that we have one large data and one small, specialized data. We train on the specialized data to get some weights. Then we…”

“Other way around,” Trevor smiled, motioning with his hands.

“Oh, right, sorry! Yeah, I remember that. So we would train on the large, broad data to get some weights. Then, for another neural network on a more specific task, we use those as the initial weights. Say, for instance, we are trying to classify objects as being Trevor or Darrell …”

“I’m Trevor Darrell!” Trevor replied.

“Yeah, I meant that those are two similar output classes, so we would need specific weights for those,” I said. I worried a bit that my joke backfired, but Trevor seemed to be in a good mood, so maybe not. I provided a half-baked concluding overview of transfer learning and neural networks in general.

“And we’re all out of time!” Trevor said, feeling satisfied.

“When do you think you can provide the results?” I asked.

“Probably tomorrow!” Trevor grinned.

I left Ruzena’s office, feeling pleased that I had remembered how convolutional neural networks worked from CS 280, but wishing that it had been explicitly listed on the syllabus. I knew I would be constantly refreshing my email tomorrow.

As it turned out, it wasn’t until another week when I got an email from Pieter saying I completely and comfortably passed the AI prelim. Now I feel a little better.